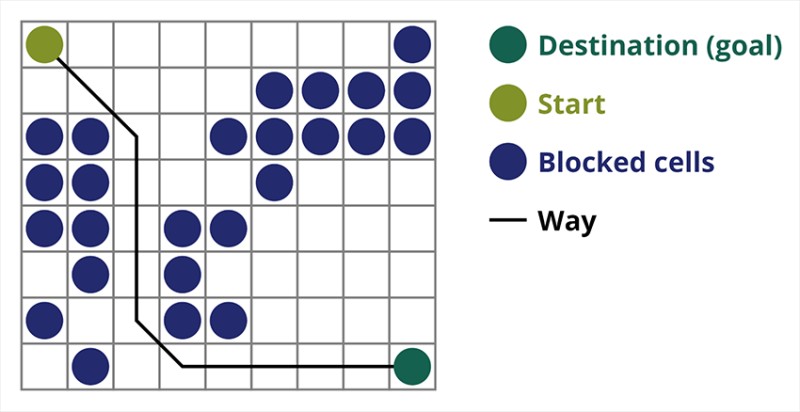
Różne algorytmy wyszukiwania są dostosowane do różnych zadań. Dzisiaj porozmawiamy o wyszukiwaniu A*, jednym z najskuteczniejszych algorytmów wyszukiwania ścieżek. Ten bardzo dobrze nadaje się do gier komputerowych i budowania wykresów wyszukiwania, takich jak drogi między miastami i tak dalej. Być może zauważyłeś na przykład w strategicznych lub taktycznych grach wideo, jak po naciśnięciu przycisku Twój gracz lub grupa natychmiast i bez opóźnień rozpoczyna przejście przez pole do określonego przez Ciebie punktu. Nie ma opóźnień właśnie dlatego, że gry wykorzystują skuteczne algorytmy, które dokładnie obliczają, w jaki sposób gracz musi się gdzieś dostać. Lub wróg, który bez wątpienia odnajdzie gracza i z daleka zacznie iść we właściwym kierunku. Zwykle do takich działań używany jest algorytm A*.
Co to jest algorytm A*
Algorytm wyszukiwania ścieżki A* jest przykładem algorytmu wyszukiwania w pierwszej kolejności. Celem algorytmu A* jest znalezienie ścieżki z jednego punktu do drugiego. Jest to jeden z klasyków wyszukiwania algorytmów grafowych. Zobaczmy, jak to działa, na przykładzie. Wyobraź sobie grę 2D z widokiem z góry. Podzielmy nasz obszar gry na kwadratowe chciwości, na przykład 8*8 komórek jak szachownica. Nasze cele mogą być jednego z dwóch typów, przejezdne lub nieprzejezdne (przeszkoda). Za każdym razem gracz lub wróg zbliżający się do gracza porusza się o jedną komórkę. W grach przejezdne komórki mogą mieć różny charakter, np. płaską drogę, trawę lub piasek, co decyduje o trudności poruszania się po nich, ale dla uproszczenia założymy, że wszystkie przejezdne komórki pokonuje się w ten sam sposób. Na poniższym obrazku niebieskie komórki to przeszkody.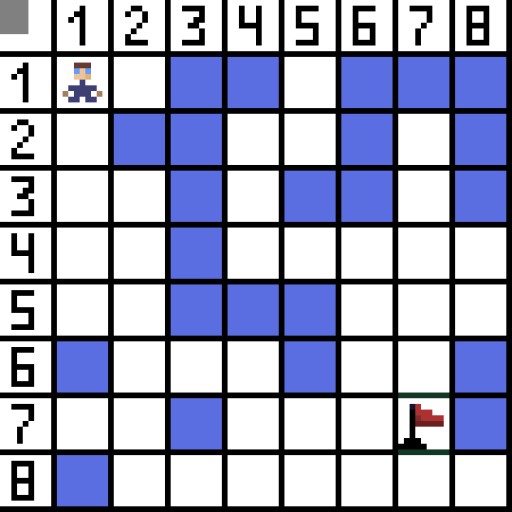
Przypiszmy jedną komórkę (lub węzeł) jako komórkę początkową (znajduje się w niej znak), a drugą komórkę jako komórkę docelową lub docelową (tą z flagą) i opiszmy, jak działa algorytm A* w tym przypadku. Znak znajduje się w komórce (1,1), a cel w komórce (7,7). Każda komórka ma sąsiadów poziomych, pionowych i ukośnych. To zależy od gry, czy policzymy węzły ukośne, czy nie. Na przykład w wielu grach z widokiem z góry, takich jak Bomberman czy Pacman, postacie mogą poruszać się tylko w poziomie lub w pionie. W tym przypadku każdy węzeł, z wyjątkiem stykania się z krawędziami, ma tylko 4 sąsiadów. Jeśli mówimy o grze, w której postacie mogą poruszać się po przekątnej, każdy węzeł może mieć maksymalnie 8 sąsiadów. W pierwszym kroku algorytmu komórka, w której znajduje się znak, ma dwóch sąsiadów. A dokładniej trzy, ale jedna z nich stanowi przeszkodę. 
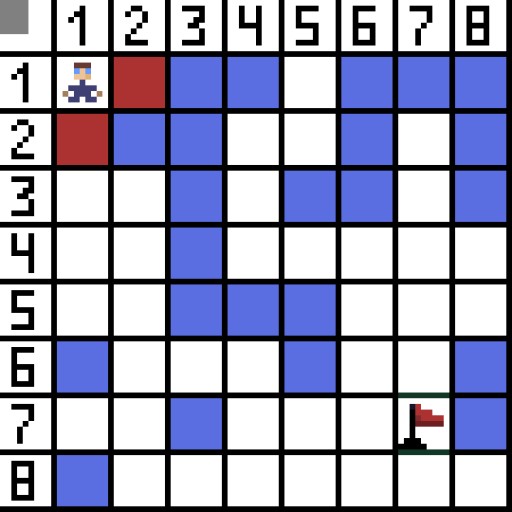Oczywiste jest, że droga ukośna jest dłuższa. jeśli ustawimy bok naszej komórki na warunkowo równy jeden, wówczas długość przekątnej tej komórki będzie równa pierwiastkowi kwadratowemu z dwóch. Tak mówi twierdzenie Pitagorasa. Aby przejść z komórki A do komórki B, należy najpierw wybrać jedną z sąsiednich komórek, a następnie następną i tak dalej. Po drodze zrozum także, czy możliwe jest przedostanie się z komórki początkowej do docelowej. Algorytm A* na każdym kroku wybiera jedną z sąsiednich komórek zgodnie z wartością funkcji F. Funkcja ta mierzy, jak dobrze komórka kandydująca ma zostać uwzględniona na naszej najkrótszej ścieżce. Jest to funkcja kosztu będąca sumą funkcji ruchu G i funkcji heurystycznej.
-
Koszt G — to odległość od węzła początkowego.
-
Koszt H (heurystyczny) to odległość od węzła końcowego (celu). Ta funkcja może być inna, programista decyduje, co jest lepsze. Być może wybór H jest najważniejszy w A* i to właśnie ten punkt sprawia, że każda konkretna implementacja algorytmu jest mniej lub bardziej skuteczna. Teoretycznie możesz użyć dowolnej funkcji.
W naszym przypadku znamy położenie komórki docelowej i możemy na przykład obliczyć geometryczną odległość euklidesową pomiędzy celem a aktualną komórką. Im krótszy dystans, tym bliżej jesteśmy celu.
-
Koszt F = G + H. Zatem algorytm oblicza koszty F wszystkich sąsiadujących węzłów i wybiera jeden z najniższych kosztów F, który będzie rozpatrywany w pierwszej kolejności. Kiedy już wybierzemy któryś z nich, oznaczamy go jako zamknięty i obliczamy wartości dla sąsiadów tego węzła.
Funkcja heurystycznaJak obliczyć H?
Jest to funkcja heurystyczna. Już sama nazwa oznacza, że jest ona zdeterminowana doświadczeniem i może być różna. Tutaj przyjmiemy to jako równe tzw. odległości euklidesowej między punktami (x1, y1) i (x2, y2):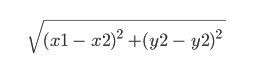
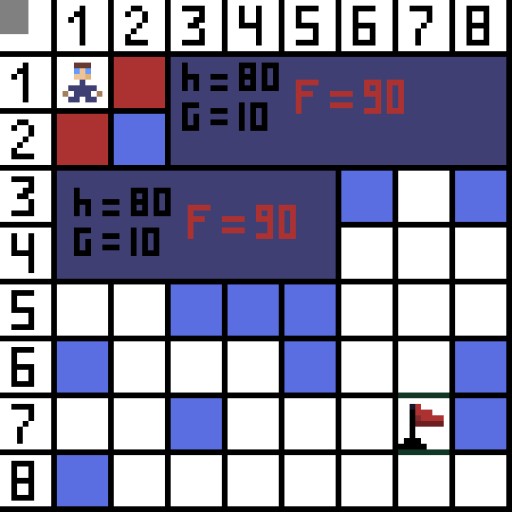Na zdjęciu w pierwszym kroku są dwie opcje i są one takie same pod względem kosztów, ale w następnym kroku postać wpada w ślepy zaułek w jednej z opcji. Dlatego idziemy w drugą stronę. W następnej iteracji mamy już 4 opcje. 
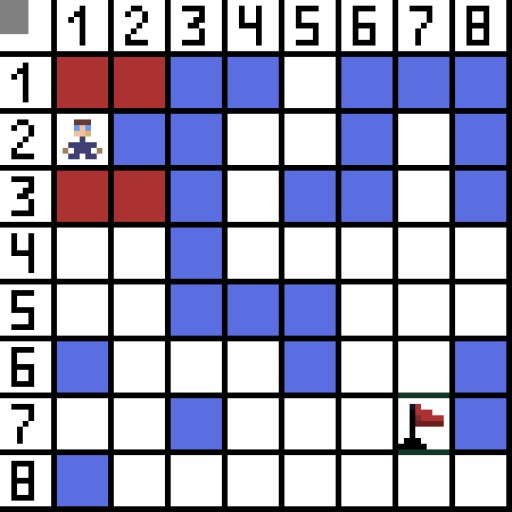Dwie z nich nie nadają się, bo prowadzą do tyłu, a pozostałe opcje są równie dobre, ale algorytm zdecydował, że najlepiej będzie iść po przekątnej do komórki (3,2). Ponadto na każdym etapie obliczenia funkcji F są powtarzane, aż znak dotrze do komórki docelowej. Jeśli oczywiście taki fragment istnieje. 
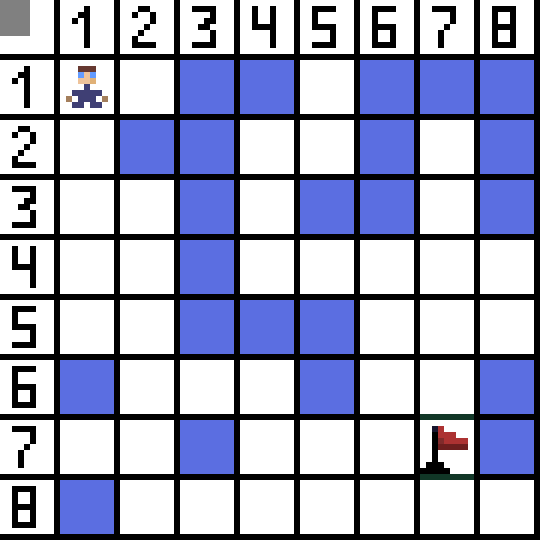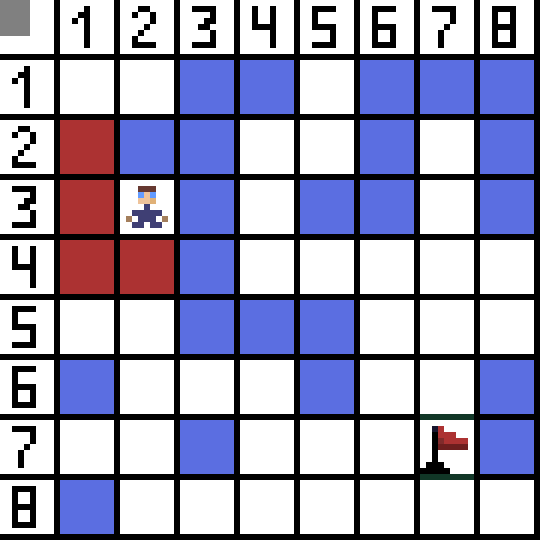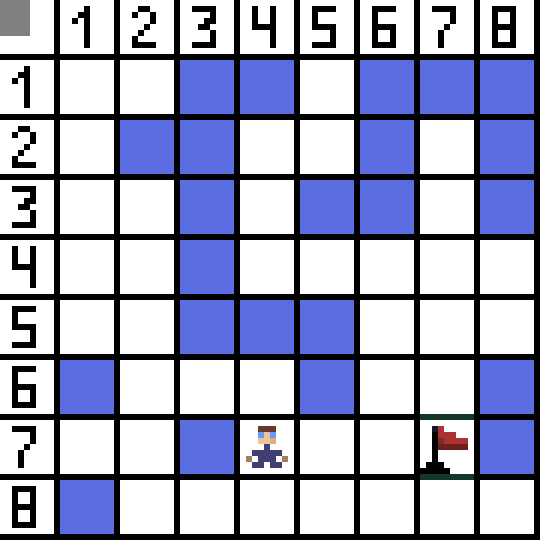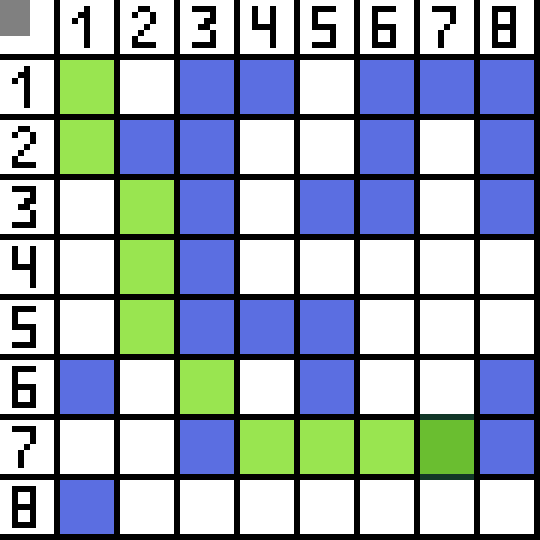Zielona droga na obrazku gif wskazuje optymalną ścieżkę postaci do flagi.
A* Algorytm krok po kroku
Aby zaimplementować algorytm w Javie, należy wykonać następujące kroki: 1. Najpierw należy utworzyć dwie listy, dla węzłów otwartych i węzłów zamkniętych. 2. Zainicjuj obie listy. Na liście zamkniętej węzeł początkowy wskazuje listę otwartą. 3. gdy na liście otwartej znajdują się elementy: 3a. Znajdź węzeł min z najmniejszym F 3b. Usuń min z otwartej listy 3c. Określ sąsiadów min (do 8, jeśli uwzględnić przekątne) 3d. Sprawdzanie każdego sąsiada: a) jeśli sąsiadem jest komórka docelowa, przestań szukać b) Jeśli nie, oblicz dla niego G, H. G = min.G + odległość między sąsiadem a min F = G + H c) jeśli węzeł o tej samej pozycji co sąsiad znajduje się na liście otwartej, a jego F jest mniejsze niż sąsiada, pomiń tego sąsiada d) jeśli węzeł o tej samej pozycji co sąsiad znajduje się na liście zamkniętej, a jego f jest mniejsze niż w przypadku sąsiada, pomiń tego sąsiada. W przeciwnym razie dodaj węzeł do otwartej listy. Koniec pętli wewnętrznej 3e. Dodanie min do zamkniętej listy Koniec pętli zewnętrznej Zatem przy każdej iteracji będziemy robić następną:- Wybierz komórkę z naszej otwartej listy z najniższym szacunkowym wynikiem całkowitym.
- Usuń tę komórkę z otwartej listy.
- Dodaj do otwartej listy wszystkie komórki, do których możemy z niego dotrzeć.
- Kiedy to robimy, przetwarzamy również nowy wynik z tego węzła do każdego nowego, aby sprawdzić, czy jest to poprawa w stosunku do tego, co mamy do tej pory, a jeśli tak, aktualizujemy wszystko, co wiemy o tej komórce.
A* Pseudokod
Oto krótki pseudokod wyszukiwania ścieżki A*:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nOd pseudokodu do implementacji A* w Javie
A* Pathfinding w realizacji Java powinien mieć pewne metody obsługujące algorytm:- Komórka, struktura przechowująca niezbędne parametry
- Listy otwarte i zamknięte
- Metoda obliczania funkcji heurystycznej
- Metoda śledzenia ścieżki od źródła do miejsca docelowego
- Metody sprawdzające, czy dana komórka jest zablokowana, czy została już osiągnięta, czy jest ważna i tak dalej
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
Ścieżka: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Widać, że jest to jedna z kilku najkrótszych ścieżek, jakie można zbudować pomiędzy tymi dwoma punktami. Zauważ, że szósty krok w naszym przykładzie na obrazku i w wynikach programu jest inny, chociaż ścieżki okazały się równie skuteczne. Program wybiera jedną z wielu najbardziej efektywnych opcji.
GO TO FULL VERSION