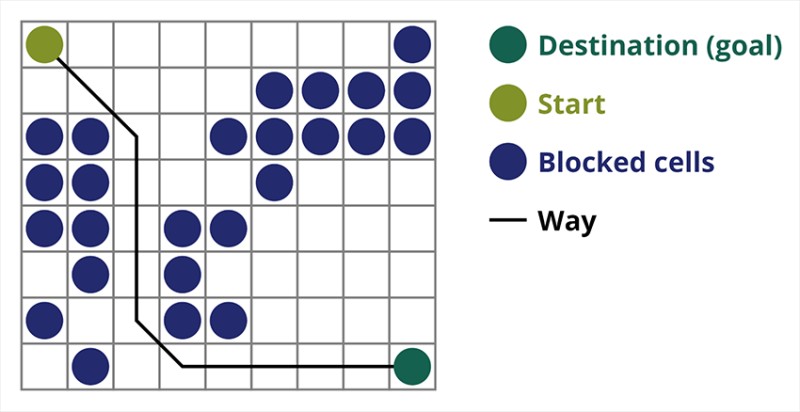
Se adaptan diferentes algoritmos de búsqueda a diferentes tareas. Hoy vamos a hablar de la búsqueda A*, uno de los algoritmos de búsqueda de rutas más eficaces. Éste es muy adecuado para juegos de computadora y para crear gráficos de búsqueda, como caminos entre ciudades, etc. Es posible que hayas notado, por ejemplo, en videojuegos estratégicos o tácticos, cómo después de presionar un botón, tu jugador o grupo comienza inmediatamente y sin demora a recorrer el campo hasta el punto que especificaste. No hay demoras precisamente porque los juegos utilizan algoritmos efectivos que calculan exactamente cómo el jugador necesita llegar a algún lugar. O un enemigo que inequívocamente encuentra al jugador y comienza a caminar en la dirección correcta desde lejos. Normalmente, para este tipo de acciones se utiliza el algoritmo A*.
¿Qué es el algoritmo A*?
El algoritmo de búsqueda de ruta A* es un ejemplo de un algoritmo de búsqueda del mejor primero. El propósito del algoritmo A* es encontrar un camino de un punto a otro. Es uno de los clásicos para buscar algoritmos de gráficos. Averigüemos cómo funciona usando un ejemplo. Imagina un juego en 2D con una vista de arriba hacia abajo. Dividamos nuestra área de juego en cuadrados de avaricia, por ejemplo, 8*8 celdas como un tablero de ajedrez. Nuestras celdas pueden ser de dos tipos, transitables o intransitables (obstáculo). Cada período de tiempo, un jugador o un enemigo que se acerca al jugador mueve una celda. En los juegos, las celdas transitables pueden ser de diferente naturaleza, por ejemplo, un camino llano, pasto o arena, lo que determina la dificultad de moverse por ellos, pero por simplicidad asumiremos que todas las celdas transitables se pasan de la misma manera. En la imagen de abajo, las celdas azules son obstáculos.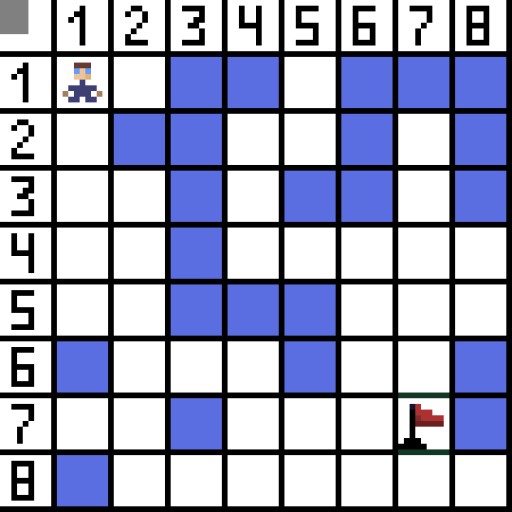
Asignemos una celda (o nodo) como celda inicial (el personaje está en ella) y la otra celda como celda objetivo o meta (la que tiene la bandera), y describamos cómo funciona el algoritmo A* para este caso. El personaje está en la celda (1,1) y el objetivo está en la celda (7,7). Cada celda tiene vecinos horizontales, verticales y diagonales. Depende del juego, si calculamos nodos diagonales o no. Por ejemplo, en muchos juegos con vista de arriba hacia abajo, como Bomberman o Pacman, los personajes sólo pueden moverse horizontal o verticalmente. En este caso, cada nodo, excepto el que toca los bordes, tiene sólo 4 vecinos. Si hablamos de un juego donde los personajes pueden moverse en diagonal, cada nodo puede tener hasta 8 vecinos. En el primer paso del algoritmo, la celda donde se encuentra el personaje tiene dos vecinos. Más precisamente, tres, pero uno de ellos es un obstáculo. 
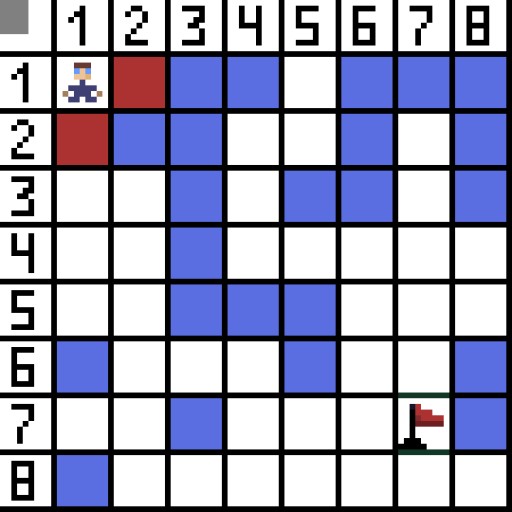Está claro que el camino diagonal es más largo. Si establecemos que el lado de nuestra celda sea condicionalmente igual a uno, entonces la longitud de la diagonal de esta celda es igual a la raíz cuadrada de dos. Esto es lo que dice el teorema de Pitágoras. Para pasar de la celda A a la celda B, primero debe seleccionar una de las celdas vecinas, luego la siguiente, y así sucesivamente. Además, en el camino, comprenda si es posible pasar de la celda inicial a la de destino. El algoritmo A* en cada paso selecciona una de las celdas vecinas de acuerdo con el valor de la función F. Esta función mide qué tan buena es una celda candidata para ser incluida en nuestro camino más corto. Esta es la función de costo y es la suma de la función de movimiento G y la función heurística.
-
Costo G: es la distancia desde un nodo inicial.
-
El costo H (heurístico) es la distancia desde el nodo final (objetivo). Esta función puede ser diferente, un desarrollador decide cuál es mejor. Quizás la elección de H sea la más importante en A*, y este es el punto que hace que cualquier implementación particular del algoritmo sea más o menos efectiva. En teoría puedes utilizar cualquier función que desees.
En nuestro caso, conocemos la posición de la celda objetivo y podemos, por ejemplo, calcular la distancia geométrica euclidiana entre la celda objetivo y la actual. Cuanto más corta sea la distancia, más cerca estaremos de la meta.
-
Costo F = G + H. Entonces, el algoritmo calcula los costos F de todos los nodos vecinos y elige uno de los costos F más bajos para observar primero. Cuando elegimos uno, lo marcamos como cerrado y calculamos los valores para los vecinos de este nodo.
Función heurística ¿Cómo podemos calcular H?
Esta es una función heurística. El nombre en sí significa que está determinado por la experiencia y puede ser diferente. Aquí la tomaremos igual a la llamada distancia euclidiana entre los puntos (x1, y1) y (x2, y2):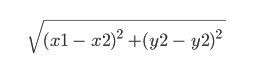
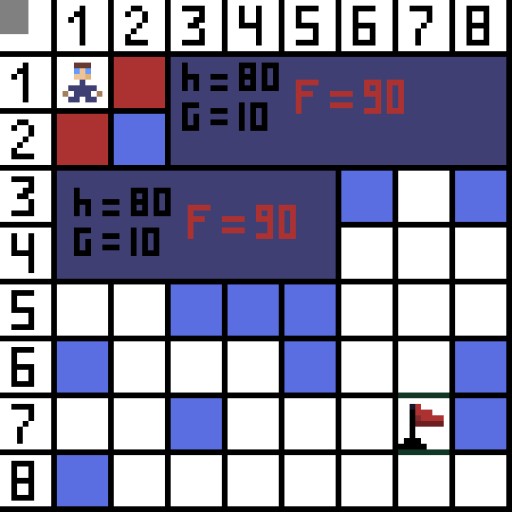En la imagen, para el primer paso, hay dos opciones y tienen el mismo costo. pero en el siguiente paso, el personaje se encuentra en un callejón sin salida en una de las opciones. Por tanto, vamos por el otro lado. En la próxima iteración, ya tenemos 4 opciones. 
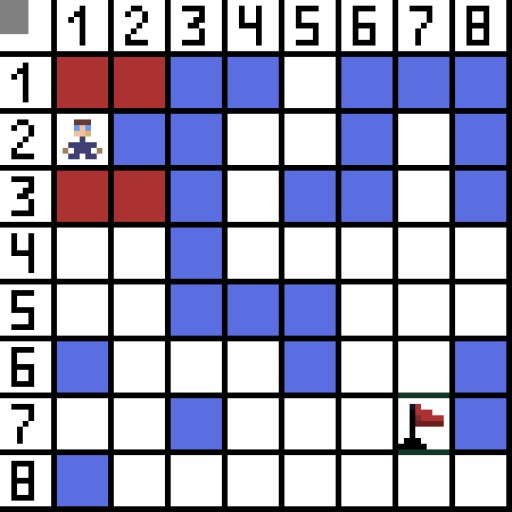Dos de ellas no son adecuadas porque conducen hacia atrás, y las otras opciones son igualmente buenas, pero el algoritmo decidió que era mejor ir en diagonal a la celda (3,2). Además, en cada paso, el cálculo de la función F se repite hasta que el personaje llega a la celda objetivo. Si, por supuesto, tal pasaje existe. 
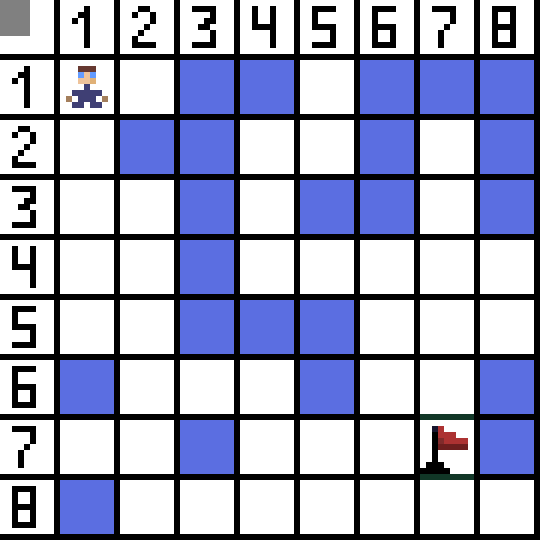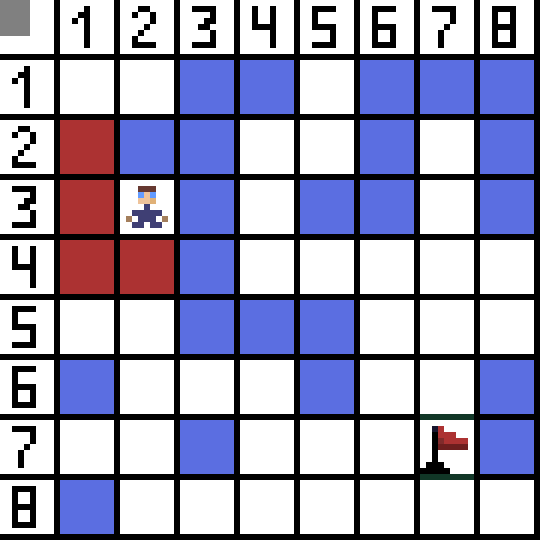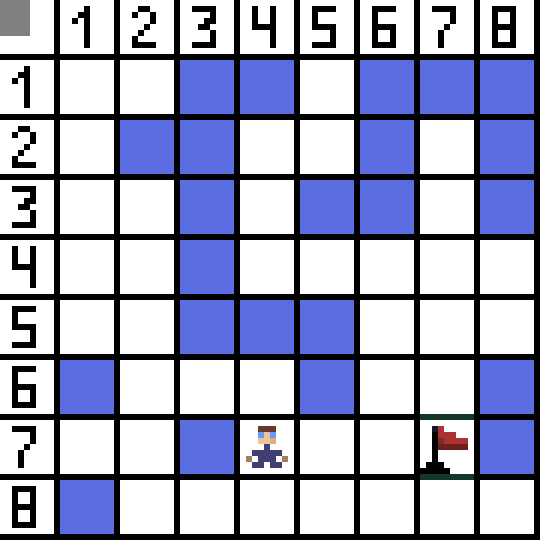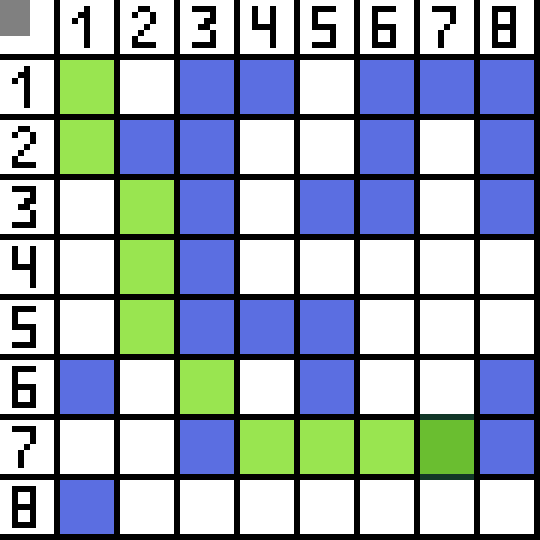La vía verde en la imagen gif indica el camino óptimo del personaje hacia la bandera.
A* Algoritmo paso a paso
Para implementar el algoritmo en Java, debe seguir los siguientes pasos: 1. Primero debe crear dos listas, para nodos abiertos y nodos cerrados. 2. Inicialice ambas listas. En una lista cerrada, el nodo inicial apunta a la lista abierta. 3. mientras haya elementos en la lista abierta: 3a. Encuentre el nodo mínimo con el F 3b más pequeño. Eliminar min de la lista abierta 3c. Determinar los vecinos mínimos (hasta 8, si se tienen en cuenta las diagonales) 3d. Verificando cada vecino: a) si el vecino es la celda objetivo, deje de buscar b) Si no, calcule G, H para ello. G = min.G + distancia entre vecino y min F = G + H c) si el nodo con la misma posición que el vecino está en la lista abierta y su F es menor que la del vecino, omitir ese vecino d) si el nodo con la misma posición que el vecino está en la lista cerrada y su f es menor que la del vecino, omita ese vecino. De lo contrario, agregue el nodo a la lista abierta. Fin del bucle interno 3e. Agregando min a la lista cerrada Fin del bucle externo Entonces, en cada iteración vamos a hacer lo siguiente:- Seleccione la celda de nuestra lista abierta con la puntuación total estimada más baja.
- Elimine esta celda de la lista abierta.
- Agregue todas las celdas a las que podamos acceder desde allí a la lista abierta.
- Cuando hacemos esto, también procesamos la nueva puntuación de ese nodo en cada uno nuevo para ver si es una mejora con respecto a lo que tenemos hasta ahora y, si lo es, actualizamos lo que sabemos sobre esa celda.
A* Pseudocódigo
Aquí hay un breve pseudocódigo de A* Pathfinding:Input: a grid with locked and empty cells, with start and goal cell.
Output: least cost path from start to goal cell.
Initialisation
openList = {startCell} //list of traversed cells
closedList = {} //list of already traversed cells
g.startCell = 0 //cost from source cell to a cell
h.startCell = h(startCell, goal) //heuristic
f.startCell = g.startCell + h.StartCell
while openList is not empty
do
//let the currentCell equal the cell with the least f value
currentCell = Cell on top of openList, with least f
if currentCell == end return
remove currentCell from openList
add currentCell to closedList
foreach n in child.currentCell
if n in closedList
continue
cost = g.currentCell + distance(currentCell,n)
if (n in openList and cost < g.n)
remove n from closedList
g.n = cost
h.n = h(n, goal)
f.n = g.n + h.nDel pseudocódigo a la implementación A* en Java
A* La realización de Pathfinding en Java debería tener algunos métodos para servir al algoritmo:- Cell, una estructura para contener los parámetros necesarios
- Listas abiertas y cerradas
- Método para calcular la función heurística.
- Método para rastrear la ruta desde el origen hasta el destino.
- Métodos para verificar si la celda dada está bloqueada, si ya fue alcanzada, si es válida, etc.
package Asterist;
import java.util.PriorityQueue;
import java.util.Stack;
public class AAsterisk {
//Java Program to implement A* Search Algorithm
//Here we're creating a shortcut for (int, int) pair
public static class Pair {
int first;
int second;
public Pair(int first, int second){
this.first = first;
this.second = second;
}
@Override
public boolean equals(Object obj) {
return obj instanceof Pair && this.first == ((Pair)obj).first && this.second == ((Pair)obj).second;
}
}
// Creating a shortcut for tuple<int, int, int> type
public static class Details {
double value;
int i;
int j;
public Details(double value, int i, int j) {
this.value = value;
this.i = i;
this.j = j;
}
}
// a Cell (node) structure
public static class Cell {
public Pair parent;
// f = g + h, where h is heuristic
public double f, g, h;
Cell()
{
parent = new Pair(-1, -1);
f = -1;
g = -1;
h = -1;
}
public Cell(Pair parent, double f, double g, double h) {
this.parent = parent;
this.f = f;
this.g = g;
this.h = h;
}
}
// method to check if our cell (row, col) is valid
boolean isValid(int[][] grid, int rows, int cols,
Pair point)
{
if (rows > 0 && cols > 0)
return (point.first >= 0) && (point.first < rows)
&& (point.second >= 0)
&& (point.second < cols);
return false;
}
//is the cell blocked?
boolean isUnBlocked(int[][] grid, int rows, int cols,
Pair point)
{
return isValid(grid, rows, cols, point)
&& grid[point.first][point.second] == 1;
}
//Method to check if destination cell has been already reached
boolean isDestination(Pair position, Pair dest)
{
return position == dest || position.equals(dest);
}
// Method to calculate heuristic function
double calculateHValue(Pair src, Pair dest)
{
return Math.sqrt(Math.pow((src.first - dest.first), 2.0) + Math.pow((src.second - dest.second), 2.0));
}
// Method for tracking the path from source to destination
void tracePath(
Cell[][] cellDetails,
int cols,
int rows,
Pair dest)
{ //A* Search algorithm path
System.out.println("The Path: ");
Stack<Pair> path = new Stack<>();
int row = dest.first;
int col = dest.second;
Pair nextNode = cellDetails[row][col].parent;
do {
path.push(new Pair(row, col));
nextNode = cellDetails[row][col].parent;
row = nextNode.first;
col = nextNode.second;
} while (cellDetails[row][col].parent != nextNode); // until src
while (!path.empty()) {
Pair p = path.peek();
path.pop();
System.out.println("-> (" + p.first + "," + p.second + ") ");
}
}
// A main method, A* Search algorithm to find the shortest path
void aStarSearch(int[][] grid,
int rows,
int cols,
Pair src,
Pair dest)
{
if (!isValid(grid, rows, cols, src)) {
System.out.println("Source is invalid...");
return;
}
if (!isValid(grid, rows, cols, dest)) {
System.out.println("Destination is invalid...");
return;
}
if (!isUnBlocked(grid, rows, cols, src)
|| !isUnBlocked(grid, rows, cols, dest)) {
System.out.println("Source or destination is blocked...");
return;
}
if (isDestination(src, dest)) {
System.out.println("We're already (t)here...");
return;
}
boolean[][] closedList = new boolean[rows][cols];//our closed list
Cell[][] cellDetails = new Cell[rows][cols];
int i, j;
// Initialising of the starting cell
i = src.first;
j = src.second;
cellDetails[i][j] = new Cell();
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = new Pair( i, j );
// Creating an open list
PriorityQueue<Details> openList = new PriorityQueue<>((o1, o2) -> (int) Math.round(o1.value - o2.value));
// Put the starting cell on the open list, set f.startCell = 0
openList.add(new Details(0.0, i, j));
while (!openList.isEmpty()) {
Details p = openList.peek();
// Add to the closed list
i = p.i; // second element of tuple
j = p.j; // third element of tuple
// Remove from the open list
openList.poll();
closedList[i][j] = true;
// Generating all the 8 neighbors of the cell
for (int addX = -1; addX <= 1; addX++) {
for (int addY = -1; addY <= 1; addY++) {
Pair neighbour = new Pair(i + addX, j + addY);
if (isValid(grid, rows, cols, neighbour)) {
if(cellDetails[neighbour.first] == null){ cellDetails[neighbour.first] = new Cell[cols]; }
if (cellDetails[neighbour.first][neighbour.second] == null) {
cellDetails[neighbour.first][neighbour.second] = new Cell();
}
if (isDestination(neighbour, dest)) {
cellDetails[neighbour.first][neighbour.second].parent = new Pair ( i, j );
System.out.println("The destination cell is found");
tracePath(cellDetails, rows, cols, dest);
return;
}
else if (!closedList[neighbour.first][neighbour.second]
&& isUnBlocked(grid, rows, cols, neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour, dest);
fNew = gNew + hNew;
if (cellDetails[neighbour.first][neighbour.second].f == -1
|| cellDetails[neighbour.first][neighbour.second].f > fNew) {
openList.add(new Details(fNew, neighbour.first, neighbour.second));
// Update the details of this
// cell
cellDetails[neighbour.first][neighbour.second].g = gNew;
//heuristic function cellDetails[neighbour.first][neighbour.second].h = hNew;
cellDetails[neighbour.first][neighbour.second].f = fNew;
cellDetails[neighbour.first][neighbour.second].parent = new Pair( i, j );
}
}
}
}
}
}
System.out.println("Failed to find the Destination Cell");
}
// test
public static void main(String[] args) {
//0: The cell is blocked
// 1: The cell is not blocked
int[][] grid = {
{ 1, 1, 0, 0, 1, 0, 0, 0 },
{ 1, 0, 0, 1, 1, 0, 1, 0 },
{ 1, 1, 0, 1, 0, 0, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 1 },
{ 1, 1, 0, 0, 0, 1, 1, 1 },
{ 0, 1, 1, 1, 0, 1, 1, 0 },
{ 1, 1, 0, 1, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1 }
};
// Start is the left-most upper-most corner
Pair src = new Pair(0,0);
//(8, 0);
// Destination is the right-most bottom-most corner
Pair dest = new Pair(6, 6);
AAsterisk app = new AAsterisk();
app.aStarSearch(grid, grid.length , grid[0].length, src, dest);
}
}
El Camino: -> (0,0) -> (1,0) -> (2,1) -> (3,1) -> (4,1) -> (5,2) -> (5, 3) -> (6,4) -> (6,5) -> (6,6)
Se puede ver que este es uno de varios caminos más cortos que se pueden construir entre estos dos puntos. Tenga en cuenta que el sexto paso en nuestro ejemplo en la imagen y en el resultado del programa es diferente, aunque las rutas resultaron ser igualmente efectivas. El programa selecciona una de las muchas opciones más efectivas.
GO TO FULL VERSION