คำถาม & คำตอบจากการสัมภาษณ์งาน: อัลกอริธึมใน Java ตอนที่ 2

นี่เป็นส่วนที่สองของภาพรวมโดยย่อของอัลกอริทึม นี่คือลิงค์ไปยังบทความแรก ก่อนหน้านี้เราได้ดูอัลกอริธึมต่างๆ สำหรับการเรียงลำดับอาร์เรย์ เช่นเดียวกับสิ่งที่เรียกว่าอัลกอริธึมโลภ วันนี้เราจะพูดถึงกราฟและอัลกอริธึมที่เกี่ยวข้องกัน กราฟเป็นหนึ่งในโครงสร้างที่ยืดหยุ่นและหลากหลายที่สุดในการเขียนโปรแกรม โดยปกติกราฟ G ถูกกำหนดโดยเซตคู่หนึ่ง เช่น G = (V, R) โดยที่:

• V คือเซตของจุดยอด
• R คือชุดของเส้นที่เชื่อมต่อคู่ของจุดยอด

เส้นเชื่อมต่อที่ไม่ได้บอกทิศทางเรียกว่าขอบ: เส้นบอกทิศทางเรียกว่าส่วนโค้ง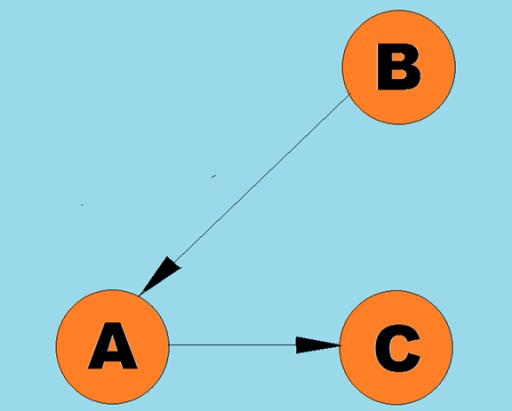โดยทั่วไปแล้ว กราฟจะแสดงด้วยแผนภาพซึ่งจุดยอดบางจุดเชื่อมต่อกันด้วยขอบ (ส่วนโค้ง) กราฟที่มีขอบแสดงทิศทางการเคลื่อนที่เรียกว่ากราฟกำกับ หากกราฟเชื่อมต่อกันด้วยขอบที่ไม่ได้ระบุทิศทางการเคลื่อนที่ เราจะบอกว่ากราฟนั้นเป็นกราฟที่ไม่มีทิศทาง ซึ่งหมายความว่าการเคลื่อนที่เป็นไปได้ในทั้งสองทิศทาง: ทั้งจากจุดยอด A ไปยังจุดยอด B และจากจุดยอด B ไปยังจุดยอด A กราฟที่เชื่อมต่อกันคือกราฟซึ่งมีเส้นทางอย่างน้อยหนึ่งเส้นทางที่นำจากแต่ละจุดยอดไปยังจุดยอดอื่น ๆ (ดังเช่นใน ตัวอย่างข้างต้น) หากไม่เป็นเช่นนั้น กราฟจะขาดการเชื่อมต่อ: สามารถกำหนดน้ำหนักให้กับขอบ (ส่วนโค้ง) ได้ น้ำหนักคือตัวเลขที่แสดงถึงระยะห่างทางกายภาพระหว่างจุดยอดสองจุด (หรือเวลาการเดินทางสัมพัทธ์ระหว่างจุดยอดสองจุด) กราฟเหล่านี้เรียกว่ากราฟถ่วงน้ำหนัก: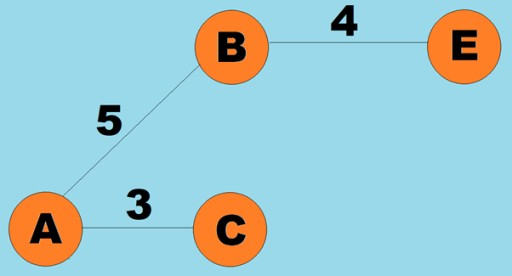

3. อัลกอริธึมการค้นหาเส้นทาง (เน้นเชิงลึก เน้นกว้างก่อน)

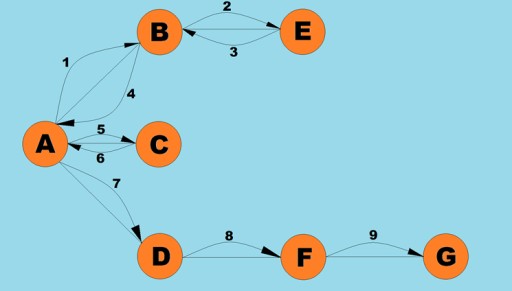
การดำเนินการพื้นฐานประการหนึ่งที่ดำเนินการกับกราฟคือการกำหนดจุดยอดทั้งหมดที่สามารถเข้าถึงได้จากจุดยอดที่กำหนด ลองนึกภาพว่าคุณกำลังพยายามพิจารณาว่าจะนั่งรถบัสจากเมืองหนึ่งไปยังอีกเมืองหนึ่งได้อย่างไร รวมถึงการเดินทางที่เป็นไปได้ด้วย บางเมืองสามารถเข้าถึงได้โดยตรง ในขณะที่บางเมืองสามารถเข้าถึงได้โดยผ่านเมืองอื่นเท่านั้น มีสถานการณ์อื่นๆ มากมายที่คุณอาจต้องค้นหาจุดยอดทั้งหมดที่คุณสามารถเข้าถึงได้จากจุดยอดที่กำหนด มีสองวิธีหลักในการสำรวจกราฟ: เชิงลึกมาก่อนและกว้างก่อน เราจะสำรวจทั้งสองสิ่งนี้ ทั้งสองวิธีจะสำรวจจุดยอดที่เชื่อมต่อกันทั้งหมด หากต้องการสำรวจอัลกอริธึมที่เน้นเชิงลึกและกว้างก่อนเพิ่มเติม เราจะใช้กราฟต่อไปนี้:

การค้นหาเชิงลึกก่อน

นี่เป็นหนึ่งในวิธีการข้ามกราฟที่ใช้กันทั่วไป กลยุทธ์ที่เน้นความลึกเป็นอันดับแรกคือการเจาะกราฟให้ลึกที่สุดเท่าที่จะเป็นไปได้ จากนั้นหลังจากถึงทางตันแล้ว เราจะกลับไปยังจุดยอดที่ใกล้ที่สุดซึ่งก่อนหน้านี้ไม่มีจุดยอดที่อยู่ติดกัน อัลกอริทึมนี้จัดเก็บข้อมูลบนสแต็กเกี่ยวกับตำแหน่งที่จะส่งคืนเมื่อถึงจุดสิ้นสุด กฎสำหรับการค้นหาเชิงลึกก่อน:

1. เยี่ยมชมจุดยอดที่อยู่ติดกันซึ่งไม่ได้เยี่ยมชมก่อนหน้านี้ ทำเครื่องหมายว่าเยี่ยมชมแล้ว และวางลงบนสแต็ก
2. ย้ายไปที่จุดยอดนี้
3. ทำซ้ำขั้นตอนที่ 1
4. หากขั้นตอนที่ 1 เป็นไปไม่ได้ ให้กลับไปที่จุดยอดก่อนหน้าแล้วลองทำตามขั้นตอนที่ 1 หากเป็นไปไม่ได้ ให้กลับไปที่จุดยอดก่อนหน้านั้นและต่อไปเรื่อยๆ จนกว่าเราจะพบจุดยอดที่เราสามารถเดินทางต่อได้
5. ทำต่อไปจนกว่าจุดยอดทั้งหมดจะอยู่บนสแต็ก

มาดูกันว่าโค้ด Java สำหรับอัลกอริทึมนี้อาจมีลักษณะอย่างไร:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

จุดยอดมีลักษณะดังนี้:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

ลองใช้อัลกอริทึมนี้กับจุดยอดเฉพาะแล้วดูว่าทำงานถูกต้องหรือไม่:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

เอาต์พุตคอนโซล: เนื่องจากเรามีเมทริกซ์ adjacency และกำลังใช้ลูปภายในลูป ความซับซ้อนของเวลาจะเป็น O(N²)

การค้นหาแบบกว้างก่อน

เช่นเดียวกับการค้นหาเชิงลึกก่อน อัลกอริธึมนี้เป็นหนึ่งในวิธีการสำรวจกราฟที่ง่ายและพื้นฐานที่สุด ประเด็นสำคัญคือเรามีจุดยอดปัจจุบันอยู่บ้าง เราใส่จุดยอดที่อยู่ติดกันที่ยังไม่ได้เยี่ยมชมทั้งหมดลงในคิวและเลือกองค์ประกอบถัดไป (ซึ่งเป็นจุดยอดที่เก็บไว้ที่ส่วนหัวของคิว) ซึ่งกลายเป็นจุดยอดปัจจุบัน... การแบ่งอัลกอริทึมนี้ออกเป็นขั้นตอน เราสามารถระบุขั้นตอนต่อไปนี้ได้:

1. เยี่ยมชมจุดยอดถัดไปที่ยังไม่ได้เยี่ยมชมซึ่งอยู่ติดกับจุดสุดยอดปัจจุบัน ทำเครื่องหมายว่าเยี่ยมชมแล้วล่วงหน้า และเพิ่มลงในคิว
2. หากไม่สามารถดำเนินการขั้นตอน #1 ได้ ให้ลบจุดยอดออกจากคิวและทำให้เป็นจุดยอดปัจจุบัน
3. หากไม่สามารถดำเนินการขั้นตอน #1 และ #2 ได้ แสดงว่าเราข้ามผ่านเสร็จแล้ว — ทุกจุดยอดถูกสำรวจแล้ว (หากเรามีกราฟที่เชื่อมโยงกัน)

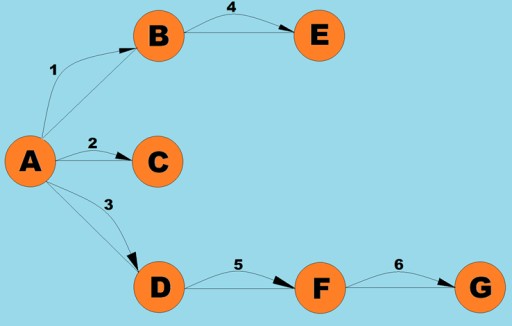คลาสกราฟที่นี่เกือบจะเหมือนกันกับคลาสที่เราใช้สำหรับอัลกอริธึมการค้นหาเชิงลึกก่อน ยกเว้นวิธีการค้นหาเองและความจริงที่ว่าคิวจะแทนที่สแต็กภายใน:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

คลาส Vertex นั้นเหมือนกับคลาสที่เราใช้กับอัลกอริธึมการค้นหาเชิงลึกเป็นอันดับแรก เรามาลองนำอัลกอริทึมนี้ไปใช้จริง:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

เอาต์พุตคอนโซล: อีกครั้ง: เรามีเมทริกซ์ adjacency และใช้ลูปที่ซ้อนกันภายในลูป ดังนั้นความซับซ้อนของเวลาของอัลกอริทึมข้างต้นคือ O(N²)

4. อัลกอริทึมของ Dijkstra

ตามที่กล่าวไว้ข้างต้น กราฟสามารถกำหนดทิศทางหรือไม่มีทิศทางได้ และคุณจะจำได้ว่าสามารถถ่วงน้ำหนักได้เช่นกัน ความสัมพันธ์ของแบบจำลองกราฟกำกับแบบถ่วงน้ำหนักที่มักพบในชีวิตจริง ตัวอย่างเช่น แผนที่เมืองที่เมืองต่างๆ เป็นจุดยอด และขอบระหว่างเมืองเหล่านั้นเป็นถนนที่มีการจราจรทางเดียวซึ่งไหลไปในทิศทางของขอบที่กำหนด สมมติว่าคุณเป็นบริษัทขนส่งสินค้า และคุณต้องค้นหาเส้นทางที่สั้นที่สุดระหว่างสองเมืองที่ห่างไกล คุณจะทำมันได้อย่างไร? การค้นหาเส้นทางที่สั้นที่สุดระหว่างจุดยอดสองจุดเป็นปัญหาที่พบบ่อยที่สุดปัญหาหนึ่งที่แก้ไขได้โดยใช้กราฟถ่วงน้ำหนัก เพื่อแก้ไขปัญหานี้ เราใช้อัลกอริทึมของ Dijkstra เมื่อคุณรันแล้ว คุณจะรู้เส้นทางที่สั้นที่สุดจากจุดยอดเริ่มต้นที่กำหนดไปยังจุดยอดอื่นๆ ขั้นตอนของอัลกอริทึมนี้มีอะไรบ้าง? ฉันจะพยายามตอบคำถามนี้ ขั้นตอนของอัลกอริทึมของ Dijkstra:

• ขั้นตอนที่ 1: ค้นหาโหนดที่อยู่ติดกันซึ่งมีต้นทุนการนำทางต่ำที่สุด (น้ำหนักขอบต่ำสุด) คุณกำลังยืนอยู่ที่จุดเริ่มต้นและคิดว่าจะไปที่ไหน: ไปยังโหนด A หรือโหนด B การย้ายไปยังแต่ละโหนดเหล่านี้มีค่าใช้จ่ายเท่าไร
• ขั้นตอนที่ 2: คำนวณระยะทางในการเดินทางไปยังเพื่อนบ้านของโหนดทั้งหมดที่อัลกอริธึมยังไม่ได้เยี่ยมชมเมื่อสำรวจขอบจาก В หากระยะทางใหม่น้อยกว่าระยะทางเก่า เส้นทางผ่านขอบ B จะกลายเป็นเส้นทางใหม่ที่สั้นที่สุดสำหรับจุดยอดนี้
• ขั้นตอนที่ 3: ทำเครื่องหมายจุดยอด B ว่าเยี่ยมชมแล้ว
• ขั้นตอนที่ 4: ไปที่ขั้นตอนที่ 1

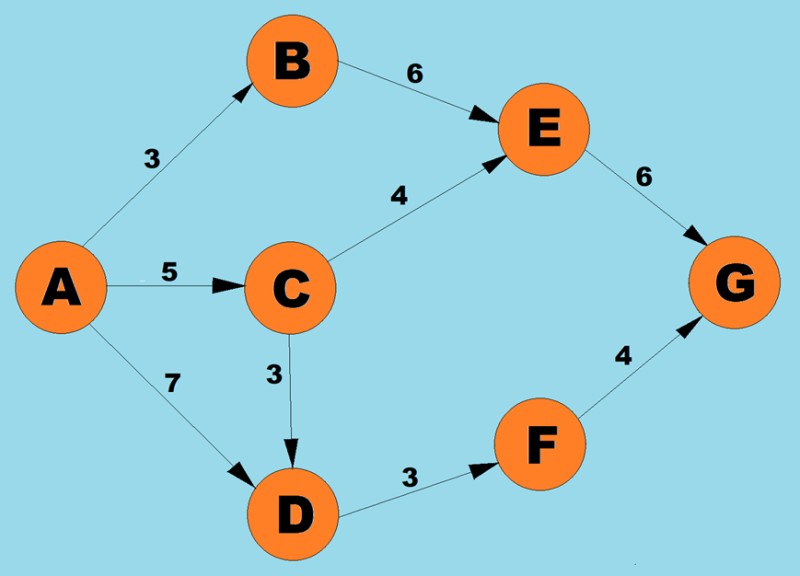เราจะทำซ้ำขั้นตอนเหล่านี้แบบวนซ้ำจนกว่าจะถึงจุดยอดทั้งหมด ลองพิจารณากราฟกำกับแบบถ่วงน้ำหนักต่อไปนี้: โดยใช้อัลกอริทึมข้างต้น เราจะกำหนดเส้นทางที่สั้นที่สุดจาก A ถึง G:

1. มีสามเส้นทางที่เป็นไปได้สำหรับจุดยอด A: ไปยัง B ที่มีน้ำหนัก 3 ถึง С ที่มีน้ำหนัก 5 และไปยัง D ที่มีน้ำหนัก 7 ตามขั้นตอนแรกของอัลกอริทึม เราเลือกโหนดที่มีต้นทุนต่ำที่สุด (น้ำหนักขอบ) ในกรณีนี้ บี.

2. เนื่องจากเพื่อนบ้านที่ไม่มีใครเยี่ยมชมเพียงคนเดียวของ B คือจุดยอด Е เราจึงตรวจสอบว่าเส้นทางจะเป็นเช่นไรหากเราผ่านจุดยอดนี้ 3(AB) + 6(พ.ศ.) = 9.

   ดังนั้นเราจึงบันทึกว่าเส้นทางที่สั้นที่สุดในปัจจุบันจาก A ถึง E คือ 9

3. เนื่องจากงานของเรากับจุดยอด B เสร็จสมบูรณ์แล้ว เราจึงดำเนินการเลือกจุดยอดถัดไปที่ขอบมีน้ำหนักขั้นต่ำ

   จากจุดยอด A และ B ความเป็นไปได้คือจุดยอด D (7), C (5) หรือ E (6)

   ขอบถึง С มีน้ำหนักน้อยที่สุด ดังนั้นเราจึงไปที่จุดยอดนี้

4. ต่อไป เช่นเคย เราจะค้นหาเส้นทางที่สั้นที่สุดไปยังจุดยอดข้างเคียงเมื่อผ่าน C:

   • AD = 5 (AC) + 3 (CD) = 8 แต่เนื่องจากเส้นทางที่สั้นที่สุดก่อนหน้า (AC = 7) น้อยกว่าเส้นทางนี้ถึง С เราจึงคงเส้นทางที่สั้นที่สุด (AC = 7) ไว้ไม่เปลี่ยนแปลง

   • CE = 5(AC) + 4(CE) = 9 เส้นทางที่สั้นที่สุดใหม่นี้เท่ากับเส้นทางก่อนหน้า ดังนั้นเราจึงปล่อยให้มันไม่มีการเปลี่ยนแปลง

5. จากจุดยอดที่ใกล้ที่สุดที่เข้าถึงได้ (E และ D) ให้เลือกจุดยอดที่มีน้ำหนักขอบน้อยที่สุด เช่น D (3)

6. เราพบเส้นทางที่สั้นที่สุดไปยังเพื่อนบ้าน F.

   AF = 7(โฆษณา) + 3(DF) = 9

7. จากจุดยอดที่ใกล้ที่สุดที่เข้าถึงได้ (E และ F) ให้เลือกจุดยอดที่มีน้ำหนักขอบน้อยที่สุด เช่น F (3)

8. ค้นหาเส้นทางที่สั้นที่สุดไปยังเพื่อนบ้าน G.

   เอจี = 7(โฆษณา) + 3(DF) + 4(FG) = 14

   ดังนั้นเราจึงพบเส้นทางจาก A ถึง G

   แต่เพื่อให้แน่ใจว่ามันสั้นที่สุด เราต้องทำตามขั้นตอนของเราบนจุดยอด E ด้วย

9. เนื่องจากจุดยอด G ไม่มีจุดยอดข้างเคียงที่ชี้ไปโดยขอบที่กำหนด เราจึงเหลือเพียงจุดยอด E เท่านั้น ดังนั้นเราจึงเลือกมัน

10. ค้นหาเส้นทางที่สั้นที่สุดไปยังเพื่อนบ้าน G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15 เส้นทางนี้ยาวกว่าเส้นทางที่สั้นที่สุดก่อนหน้า (AG (14)) ดังนั้นเราจึงปล่อยให้เส้นทางนี้ไม่เปลี่ยนแปลง

    เนื่องจากไม่มีจุดยอดที่นำจาก G จึงไม่สมเหตุสมผลที่จะรันขั้นตอนบนอัลกอริทึมบนจุดยอดนี้ นั่นหมายความว่าการทำงานของอัลกอริธึมเสร็จสมบูรณ์

ดังที่ได้กล่าวไปแล้วข้างต้น นอกเหนือจากการค้นหาเส้นทางที่สั้นที่สุดสำหรับ AG แล้ว เรายังได้รับเส้นทางที่สั้นที่สุดจากจุดยอด A ไปยังจุดยอดอื่นๆ (AB, AC, AD, AE, AF) ตอนนี้ถึงเวลามาดูกันว่าสิ่งนี้สามารถทำได้ใน Java อย่างไร เริ่มจากคลาสจุดยอดกันก่อน:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

คลาสจุดสุดยอดแทบจะเหมือนกับคลาสจุดสุดยอดที่ใช้สำหรับการค้นหาแบบกว้างก่อน ในการแสดงเส้นทางที่สั้นที่สุด เราจำเป็นต้องมีคลาสใหม่ที่จะมีข้อมูลที่เราต้องการ:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

ในชั้นเรียนนี้ เราจะเห็นระยะทางรวมของเส้นทางและจุดยอดที่จะเคลื่อนที่เมื่อผ่านไปตามเส้นทางที่สั้นที่สุด ทีนี้ลองดูคลาสที่เราสำรวจเส้นทางที่สั้นที่สุดผ่านกราฟกัน ดังนั้นเราจึงมีคลาสกราฟ:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

นั่นคือความมหัศจรรย์ทั้งหมด =) ตอนนี้เรามาดูการทำงานของอัลกอริทึมนี้กัน:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

และเอาต์พุตคอนโซลคือ: ความซับซ้อนของเวลาของอัลกอริธึมนี้ไม่ใช่ใครอื่นนอกจาก O(N²) เนื่องจากเรามีลูปที่ซ้อนกัน นั่นคือทั้งหมดที่ฉันมีวันนี้ ขอบคุณสำหรับความสนใจ!