Les questions-réponses des entretiens d'embauche : les algorithmes en Java, partie 2

Ceci est la deuxième partie d’un bref aperçu des algorithmes. Voici un lien vers le premier article . Plus tôt, nous avons examiné divers algorithmes de tri des tableaux ainsi que l'algorithme dit glouton. Aujourd'hui, nous allons parler des graphiques et des algorithmes qui leur sont associés. Un graphique est l’une des structures les plus flexibles et polyvalentes de la programmation. Le graphe G est généralement défini par une paire d'ensembles, soit G = (V, R), où :

• V est un ensemble de sommets ;
• R est un ensemble de lignes reliant des paires de sommets.

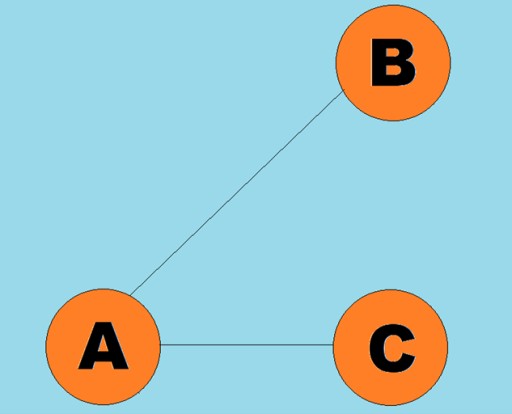Les lignes de connexion non orientées sont appelées arêtes : Les lignes orientées sont appelées arcs : 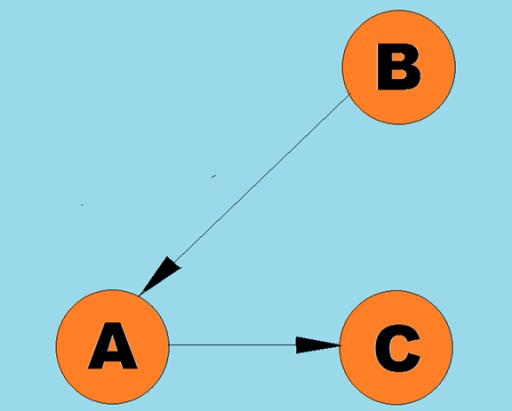Généralement, un graphique est représenté par un diagramme dans lequel certains des sommets sont reliés par des arêtes (arcs). Les graphiques dont les bords indiquent une direction de parcours sont appelés graphiques orientés. Si un graphe est relié par des arêtes qui n’indiquent pas la direction du parcours, alors on dit qu’il s’agit d’un graphe non orienté. Cela signifie que le mouvement est possible dans les deux directions : à la fois du sommet A au sommet B et du sommet B au sommet A. Un graphe connexe est un graphe dans lequel au moins un chemin mène de chaque sommet à n'importe quel autre sommet (comme dans le exemple ci-dessus). Si ce n’est pas le cas, alors le graphique est dit déconnecté : 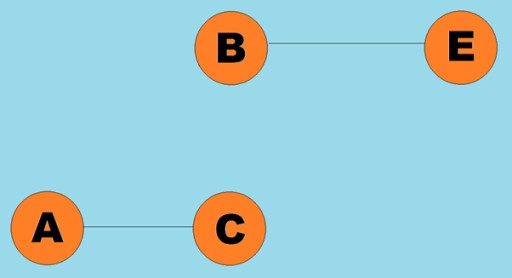des poids peuvent également être attribués aux arêtes (arcs). Les poids sont des nombres qui représentent, par exemple, la distance physique entre deux sommets (ou le temps de trajet relatif entre deux sommets). Ces graphiques sont appelés graphiques pondérés :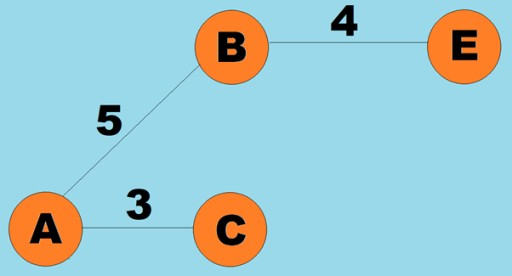

3. Algorithmes de recherche de chemin (profondeur d'abord, largeur d'abord)

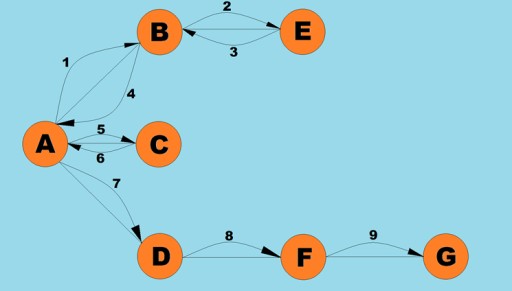
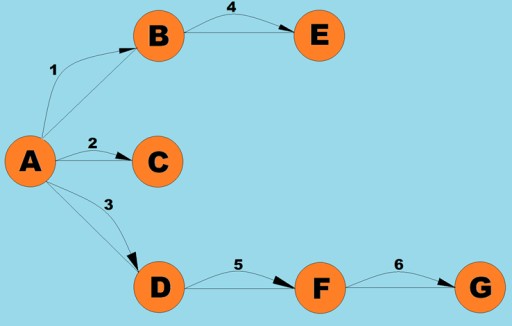
L'une des opérations de base effectuées avec les graphiques consiste à déterminer tous les sommets accessibles à partir d'un sommet donné. Imaginez que vous essayez de déterminer comment vous pouvez prendre un bus d'une ville à une autre, y compris les transferts possibles. Certaines villes sont accessibles directement, tandis que d'autres ne peuvent être atteintes qu'en passant par d'autres villes. Il existe de nombreuses autres situations dans lesquelles vous devrez peut-être trouver tous les sommets que vous pouvez atteindre à partir d'un sommet donné. Il existe deux manières principales de parcourir les graphiques : la profondeur d'abord et la largeur d'abord. Nous allons explorer ces deux éléments. Les deux méthodes parcourent tous les sommets connectés. Pour explorer davantage les algorithmes de profondeur d'abord et de largeur d'abord, nous utiliserons le graphique suivant :

Recherche en profondeur d'abord

Il s’agit de l’une des méthodes de parcours graphique les plus courantes. La stratégie axée sur la profondeur consiste à aller le plus profondément possible dans un graphique. Ensuite, après avoir atteint une impasse, nous retournons au sommet le plus proche qui possède des sommets adjacents non visités auparavant. Cet algorithme stocke des informations sur la pile indiquant où revenir lorsqu'une impasse est atteinte. Règles pour la recherche en profondeur :

1. Visitez un sommet adjacent non visité auparavant, marquez-le comme visité et placez-le sur la pile.
2. Déplacez-vous vers ce sommet.
3. Répétez l'étape 1.
4. Si l'étape 1 est impossible, revenez au sommet précédent et essayez d'effectuer l'étape 1. Si cela n'est pas possible, revenez au sommet précédent celui-ci, et ainsi de suite, jusqu'à ce que nous trouvions un sommet à partir duquel nous pouvons continuer le parcours.
5. Continuez jusqu'à ce que tous les sommets soient sur la pile.

Voyons à quoi pourrait ressembler le code Java de cet algorithme :

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

Un sommet ressemble à ceci :

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

Exécutons cet algorithme avec des sommets spécifiques et voyons s'il fonctionne correctement :

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

Sortie de la console : Puisque nous avons une matrice de contiguïté et que nous utilisons une boucle dans une boucle, la complexité temporelle sera O(N²).

Recherche en largeur

Comme la recherche en profondeur d’abord, cet algorithme est l’une des méthodes de parcours graphique les plus simples et les plus basiques. L'essentiel est que nous avons un sommet actuel. Nous mettons tous ses sommets adjacents non visités dans une file d'attente et sélectionnons l'élément suivant (qui est le sommet stocké en tête de la file d'attente), qui devient le sommet actuel… En divisant cet algorithme en étapes, nous pouvons identifier les étapes suivantes :

1. Visitez le sommet suivant non visité précédemment, adjacent au sommet actuel, marquez-le comme visité à l'avance et ajoutez-le à la file d'attente.
2. Si l'étape 1 ne peut pas être effectuée, supprimez le sommet de la file d'attente et faites-en le sommet actuel.
3. Si les étapes 1 et 2 ne peuvent pas être effectuées, alors nous avons terminé le parcours — chaque sommet a été parcouru (si nous avons un graphe connecté).

La classe graphique ici est presque identique à celle que nous avons utilisée pour l'algorithme de recherche en profondeur d'abord, à l'exception de la méthode de recherche elle-même et du fait qu'une file d'attente remplace la pile interne :

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

La classe Vertex est identique à celle que nous avons utilisée avec l'algorithme de recherche en profondeur d'abord. Mettons cet algorithme en action :

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

Sortie de la console : Encore une fois : nous avons une matrice de contiguïté et utilisons une boucle imbriquée dans une boucle, donc la complexité temporelle de l'algorithme ci-dessus est O(N²).

4. L'algorithme de Dijkstra

Comme mentionné précédemment, les graphiques peuvent être orientés ou non. Et vous vous souviendrez qu’ils peuvent aussi être pondérés. Les graphiques orientés et pondérés modélisent les relations que l'on retrouve souvent dans la vie réelle : par exemple, une carte de villes où les villes sont des sommets et les bords entre eux sont des routes à sens unique, circulant dans la direction du bord dirigé. Disons que vous êtes une entreprise de fret et que vous devez trouver l'itinéraire le plus court entre deux villes éloignées. Comment feriez-vous? Trouver le chemin le plus court entre deux sommets est l'un des problèmes les plus courants résolus à l'aide de graphiques pondérés. Pour résoudre ce problème, nous utilisons l'algorithme de Dijkstra. Une fois que vous l'aurez exécuté, vous connaîtrez les chemins les plus courts d'un sommet initial donné à tous les autres. Quelles sont les étapes de cet algorithme ? Je vais essayer de répondre à cette question. Étapes de l'algorithme de Dijkstra :

• Étape 1 : recherchez le nœud adjacent dont le coût de navigation est le plus bas (poids de bord le plus faible). Vous vous trouvez au tout début et vous demandez où aller : vers le nœud A ou le nœud B. Quel est le coût du déplacement vers chacun de ces nœuds ?
• Étape 2 : calculer la distance à parcourir jusqu'à tous les voisins du nœud В qui n'ont pas encore été visités par l'algorithme lors de la traversée du bord depuis В. Si la nouvelle distance est inférieure à l’ancienne, alors le chemin passant par l’arête B devient le nouveau chemin le plus court pour ce sommet.
• Étape 3 : marquez le sommet B comme visité.
• Étape 4 : Passez à l'étape 1.

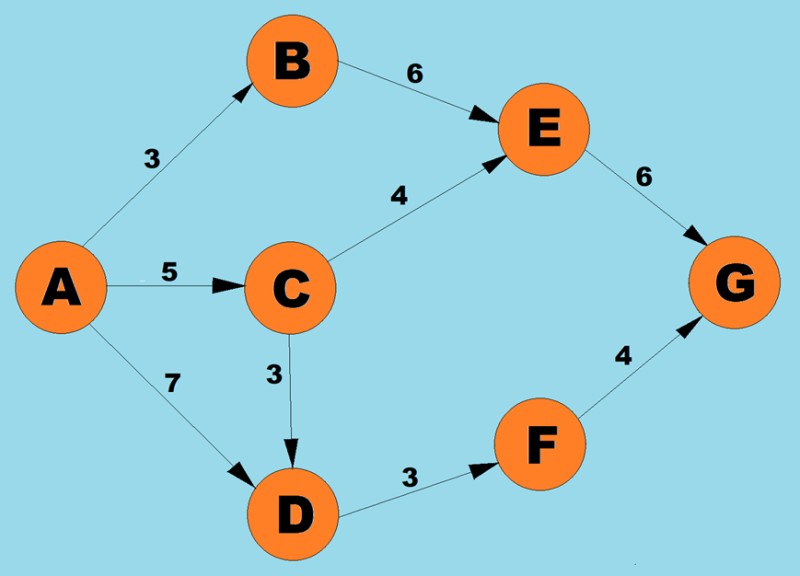Nous répéterons ces étapes en boucle jusqu'à ce que tous les sommets aient été visités. Considérons le graphe orienté pondéré suivant : En utilisant l'algorithme ci-dessus, nous déterminerons le chemin le plus court de A à G :

1. Il existe trois chemins possibles pour le sommet A : vers B avec un poids de 3, vers С avec un poids de 5 et vers D avec un poids de 7. Selon la première étape de l'algorithme, nous sélectionnons le nœud avec le coût le plus bas (poids du bord). Dans ce cas, B.

2. Puisque le seul voisin non visité de B est le sommet Е, nous vérifions quel serait le chemin si nous passions par ce sommet. 3(AB) + 6(BE) = 9.

   Ainsi, nous enregistrons que le chemin le plus court actuel de A à E est 9.

3. Puisque notre travail avec le sommet B est terminé, nous procédons à la sélection du prochain sommet dont l’arête a le poids minimum.

   A partir des sommets A et B, les possibilités sont les sommets D (7), C (5) ou E (6).

   L’arête vers С a le plus petit poids, nous allons donc à ce sommet.

4. Ensuite, comme précédemment, nous trouvons le chemin le plus court vers les sommets voisins en passant par C :

   • AD = 5 (AC) + 3 (CD) = 8, mais comme le chemin le plus court précédent (AC = 7) est inférieur à celui-ci passant par С, on garde le chemin le plus court (AC = 7) inchangé.

   • CE = 5(AC) + 4(CE) = 9. Ce nouveau chemin le plus court est égal au précédent, nous le laissons donc également inchangé.

5. Parmi les sommets accessibles les plus proches (E et D), sélectionnez le sommet avec le plus petit poids d'arête, soit D (3).

6. On trouve le chemin le plus court vers son voisin F.

   AF = 7(AD) + 3(DF) = 9

7. Parmi les sommets accessibles les plus proches (E et F), sélectionnez le sommet avec le plus petit poids d'arête, c'est-à-dire F (3).

8. Trouver le chemin le plus court vers son voisin G.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   Nous avons donc trouvé un chemin de A à G.

   Mais pour être sûr qu'il soit le plus court, il faut aussi effectuer nos pas sur le sommet E.

9. Parce que le sommet G n’a pas de sommets voisins pointés par des arêtes dirigées, il ne nous reste que le sommet E, nous le choisissons donc.

10. Trouvez le chemin le plus court vers le voisin G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Ce chemin est plus long que le chemin le plus court précédent (AG (14)), nous laissons donc ce chemin inchangé.

    Puisqu’il n’y a aucun sommet partant de G, cela n’a aucun sens d’exécuter les étapes de l’algorithme sur ce sommet. Cela signifie que le travail de l’algorithme est terminé.

Comme je l'ai dit plus tôt, en plus de trouver le chemin le plus court pour AG, nous avons également obtenu les chemins les plus courts du sommet A à tous les autres sommets (AB, AC, AD, AE, AF). Eh bien, il est maintenant temps de voir comment cela peut être réalisé en Java. Commençons par la classe vertex :

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

La classe de sommets est pratiquement identique à la classe de sommets utilisée pour la recherche en largeur d'abord. Pour afficher les chemins les plus courts, nous avons besoin d'une nouvelle classe qui contiendra les données dont nous avons besoin :

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

Dans cette classe, nous pouvons voir la distance totale du chemin et les sommets qui seront parcourus en passant par le chemin le plus court. Et maintenant, regardons la classe dans laquelle nous parcourons réellement le chemin le plus court à travers le graphique. Nous avons donc ici la classe Graph :

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

C'est donc toute la magie =) Maintenant, jetons un coup d'œil à cet algorithme en action :

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

Et le résultat de la console est le suivant : La complexité temporelle de cet algorithme n’est autre que O(N²), puisque nous avons des boucles imbriquées. C'est tout ce que j'ai aujourd'hui. Merci de votre attention!