As perguntas e respostas das entrevistas de emprego: algoritmos em Java, parte 2

Esta é a segunda parte de uma breve visão geral dos algoritmos. Aqui está um link para o primeiro artigo . Anteriormente, examinamos vários algoritmos para classificação de arrays, bem como o chamado algoritmo ganancioso. Hoje falaremos sobre gráficos e os algoritmos associados a eles. Um gráfico é uma das estruturas mais flexíveis e versáteis da programação. O gráfico G é geralmente definido por um par de conjuntos, ou seja, G = (V, R), onde:

• V é um conjunto de vértices;
• R é um conjunto de linhas conectando pares de vértices.

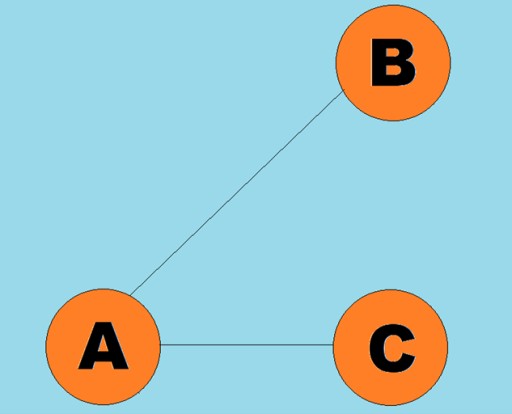As linhas de conexão não direcionadas são chamadas de arestas: As linhas direcionadas são chamadas de arcos: 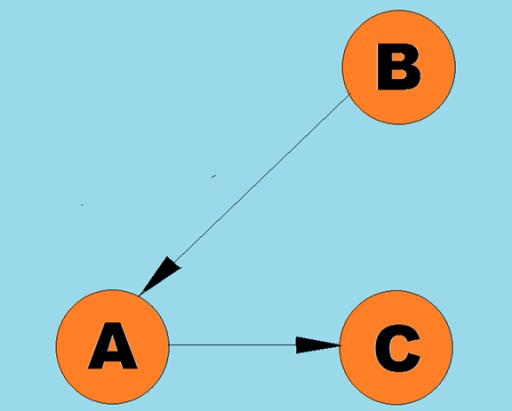Normalmente, um gráfico é representado por um diagrama no qual alguns dos vértices são conectados por arestas (arcos). Os gráficos cujas arestas indicam uma direção de travessia são chamados de gráficos direcionados. Se um grafo é conectado por arestas que não indicam a direção do percurso, então dizemos que é um grafo não direcionado. Isso significa que o movimento é possível em ambas as direções: tanto do vértice A para o vértice B, quanto do vértice B para o vértice A. Um grafo conectado é um grafo no qual pelo menos um caminho leva de cada vértice a qualquer outro vértice (como no exemplo acima). Se este não for o caso, então o gráfico é dito desconectado: 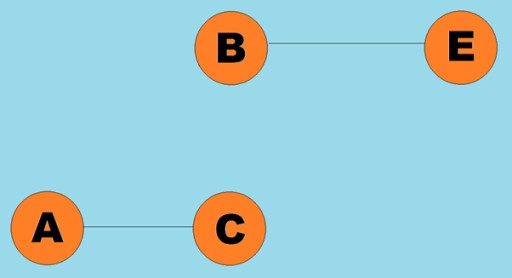Pesos também podem ser atribuídos às arestas (arcos). Os pesos são números que representam, por exemplo, a distância física entre dois vértices (ou o tempo relativo de viagem entre dois vértices). Esses gráficos são chamados de gráficos ponderados: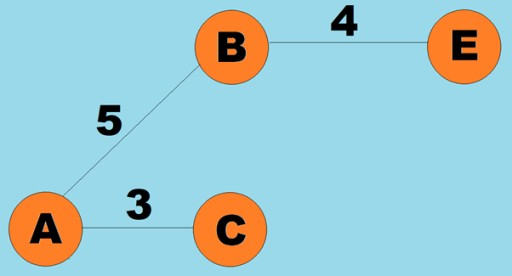

3. Algoritmos de descoberta de caminhos (primeiro em profundidade, primeiro em largura)

Uma das operações básicas realizadas com grafos é determinar todos os vértices alcançáveis ​​a partir de um determinado vértice. Imagine que você está tentando determinar como pode pegar um ônibus de uma cidade para outra, incluindo possíveis transferências. Algumas cidades podem ser alcançadas diretamente, enquanto outras só podem ser alcançadas passando por outras cidades. Existem muitas outras situações em que você pode precisar encontrar todos os vértices que pode alcançar a partir de um determinado vértice. Existem duas maneiras principais de percorrer gráficos: primeiro em profundidade e primeiro em largura. Exploraremos ambos. Ambos os métodos atravessam todos os vértices conectados. Para explorar ainda mais os algoritmos de profundidade e largura, usaremos o seguinte gráfico:

Pesquisa em profundidade

Este é um dos métodos de travessia de gráfico mais comuns. A estratégia de profundidade é ir o mais fundo possível em um gráfico. Então, após chegar a um beco sem saída, retornamos ao vértice mais próximo que possui vértices adjacentes não visitados anteriormente. Este algoritmo armazena informações na pilha sobre para onde retornar quando um beco sem saída for atingido. Regras para pesquisa em profundidade:

1. Visite um vértice adjacente não visitado anteriormente, marque-o como visitado e coloque-o na pilha.
2. Vá para este vértice.
3. Repita o passo 1.
4. Se o passo 1 for impossível, retorne ao vértice anterior e tente realizar o passo 1. Se isso não for possível, retorne ao vértice anterior a esse, e assim por diante, até encontrarmos um vértice a partir do qual possamos continuar a travessia.
5. Continue até que todos os vértices estejam na pilha.

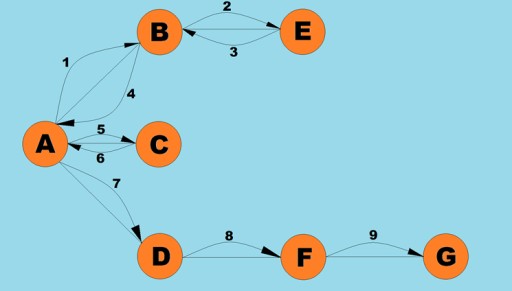Vamos dar uma olhada na aparência do código Java para esse algoritmo:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

Um vértice se parece com isto:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

Vamos executar este algoritmo com vértices específicos e ver se funciona corretamente:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

Saída do console: Como temos uma matriz de adjacência e estamos usando um loop dentro de um loop, a complexidade do tempo será O(N²).

Pesquisa ampla

Assim como a pesquisa em profundidade, esse algoritmo é um dos métodos mais simples e básicos de travessia de grafos. A essência é que temos algum vértice atual. Colocamos todos os seus vértices adjacentes não visitados em uma fila e selecionamos o próximo elemento (que é o vértice armazenado no topo da fila), que se torna o vértice atual… Dividindo esse algoritmo em etapas, podemos identificar as seguintes etapas:

1. Visite o próximo vértice não visitado anteriormente adjacente ao vértice atual, marque-o como visitado antecipadamente e adicione-o à fila.
2. Se a etapa 1 não puder ser executada, remova o vértice da fila e torne-o o vértice atual.
3. Se as etapas 1 e 2 não puderem ser executadas, então concluímos a travessia - todos os vértices foram percorridos (se tivermos um gráfico conectado).

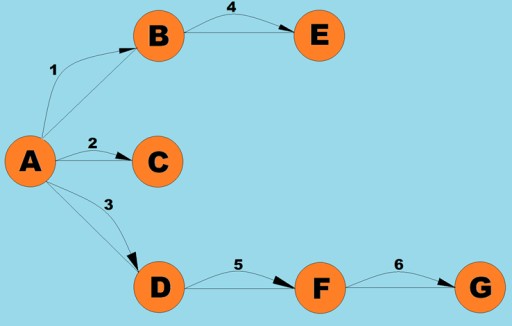A classe de gráfico aqui é quase idêntica àquela que usamos para o algoritmo de busca em profundidade, exceto pelo próprio método de busca e pelo fato de que uma fila substitui a pilha interna:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

A classe Vertex é idêntica àquela que usamos com o algoritmo de busca em profundidade. Vamos colocar esse algoritmo em ação:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

Saída do console: Novamente: temos uma matriz de adjacência e usamos um loop aninhado dentro de um loop, então a complexidade de tempo do algoritmo acima é O(N²).

4. Algoritmo de Dijkstra

Conforme mencionado anteriormente, os gráficos podem ser direcionados ou não direcionados. E você deve se lembrar que eles também podem ser ponderados. Gráficos direcionados e ponderados modelam relacionamentos frequentemente encontrados na vida real: por exemplo, um mapa de cidades onde as cidades são vértices e as arestas entre elas são estradas com tráfego de mão única, fluindo na direção da aresta direcionada. Digamos que você seja uma empresa de frete e precise encontrar o caminho mais curto entre duas cidades distantes. Como você faria? Encontrar o caminho mais curto entre dois vértices é um dos problemas mais comuns resolvidos por meio de gráficos ponderados. Para resolver este problema, usamos o algoritmo de Dijkstra. Depois de executá-lo, você conhecerá os caminhos mais curtos de um determinado vértice inicial para todos os outros. Quais são as etapas deste algoritmo? Vou tentar responder a esta pergunta. Etapas do algoritmo de Dijkstra:

• Etapa 1: Encontre o nó adjacente que tem o menor custo para navegar (menor peso de aresta). Você está bem no início e pensando para onde ir: para o nó A ou para o nó B. Qual é o custo de mudar para cada um desses nós?
• Etapa 2: calcule a distância a percorrer até todos os vizinhos do nó B que ainda não foram visitados pelo algoritmo ao atravessar a aresta de B. Se a nova distância for menor que a antiga, então o caminho através da aresta B torna-se o novo caminho mais curto para este vértice.
• Passo 3: marque o vértice B como visitado.
• Etapa 4: vá para a etapa 1.

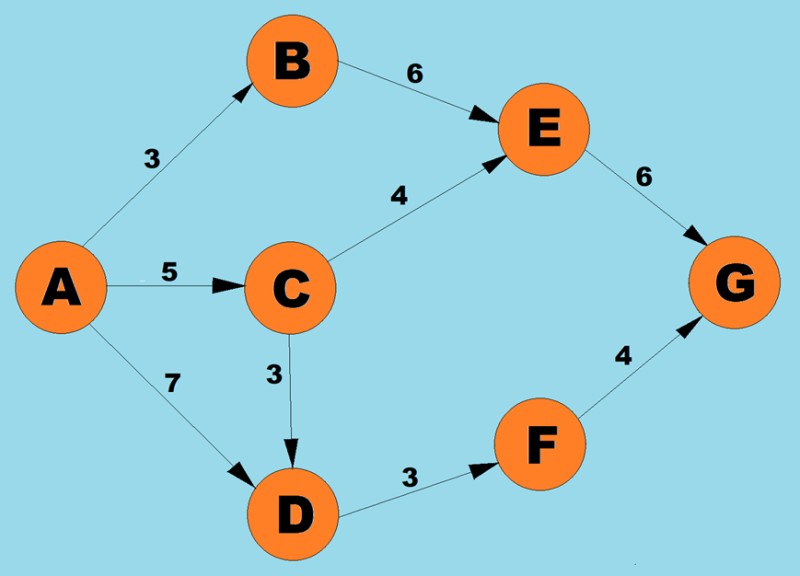Repetiremos essas etapas em loop até que todos os vértices tenham sido visitados. Vamos considerar o seguinte gráfico direcionado ponderado: Usando o algoritmo acima, determinaremos o caminho mais curto de A a G:

1. Existem três caminhos possíveis para o vértice A: para B com peso 3, para С com peso 5 e para D com peso 7. De acordo com a primeira etapa do algoritmo, selecionamos o nó com menor custo (peso da aresta). Neste caso, B.

2. Como o único vizinho não visitado de B é o vértice E, verificamos qual seria o caminho se passássemos por esse vértice. 3(AB) + 6(BE) = 9.

   Assim, registramos que o caminho mais curto atual de A a E é 9.

3. Como nosso trabalho com o vértice B está concluído, procedemos à seleção do próximo vértice cuja aresta tenha o peso mínimo.

   Dos vértices A e B, as possibilidades são os vértices D (7), C (5) ou E (6).

   A aresta de C tem o menor peso, então vamos para este vértice.

4. A seguir, como antes, encontramos o caminho mais curto para os vértices vizinhos ao passar por C:

   • AD = 5 (AC) + 3 (CD) = 8, mas como o caminho mais curto anterior (AC = 7) é menor que este através de С, mantemos o caminho mais curto (AC = 7) inalterado.

   • CE = 5(AC) + 4(CE) = 9. Este novo caminho mais curto é igual ao anterior, portanto também o deixamos inalterado.

5. A partir dos vértices acessíveis mais próximos (E e D), selecione o vértice com o menor peso de aresta, ou seja, D (3).

6. Encontramos o caminho mais curto para seu vizinho F.

   AF = 7(AD) + 3(DF) = 9

7. A partir dos vértices acessíveis mais próximos (E e F), selecione o vértice com o menor peso de aresta, ou seja, F (3).

8. Encontre o caminho mais curto para seu vizinho G.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   Então, encontramos um caminho de A a G.

   Mas para ter certeza de que é o mais curto, devemos também realizar nossos passos no vértice E.

9. Como o vértice G não possui vértices vizinhos apontados por arestas direcionadas, resta apenas o vértice E, então o escolhemos.

10. Encontre o caminho mais curto para o vizinho G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Este caminho é mais longo que o caminho mais curto anterior (AG (14)), então deixamos este caminho inalterado.

    Como não há vértices partindo de G, não faz sentido executar as etapas do algoritmo neste vértice. Isso significa que o trabalho do algoritmo está completo.

Como disse anteriormente, além de encontrar o caminho mais curto para AG, também obtivemos os caminhos mais curtos do vértice A para todos os outros vértices (AB, AC, AD, AE, AF). Bem, agora é hora de dar uma olhada em como isso pode ser feito em Java. Vamos começar com a classe vértice:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

A classe de vértice é virtualmente idêntica à classe de vértice usada para pesquisa em largura. Para exibir os caminhos mais curtos, precisamos de uma nova classe que conterá os dados que precisamos:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

Nesta classe podemos ver a distância total do caminho e os vértices que serão percorridos ao passar pelo caminho mais curto. E agora vamos dar uma olhada na classe onde realmente percorremos o caminho mais curto no gráfico. Então aqui temos a classe Graph:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

Então essa é toda a mágica =) Agora, vamos dar uma olhada neste algoritmo em ação:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

E a saída do console é esta: A complexidade de tempo deste algoritmo não é outra senão O(N²), uma vez que temos loops aninhados. Isso é tudo que tenho hoje. Agradecimentos para sua atenção!