就職面接の Q&A: Java のアルゴリズム、パート 2

これはアルゴリズムの概要の 2 番目の部分です。最初の記事 へのリンクはこちらです。 先ほど、配列をソートするためのさまざまなアルゴリズムと、いわゆる貪欲アルゴリズムについて説明しました。今日はグラフとそれに関連するアルゴリズムについて話します。グラフは、プログラミングにおいて最も柔軟で多用途な構造の 1 つです。グラフ G は通常、セットのペア、つまり G = (V, R) によって定義されます。ここで、

• V は頂点のセットです。
• R は、頂点のペアを接続する線のセットです。

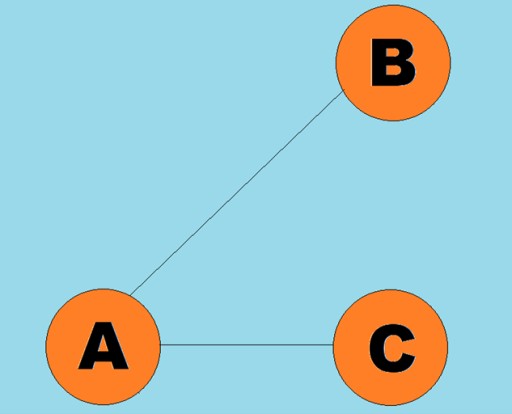無向の接続線はエッジと呼ばれます。有向線は円弧と呼ばれます。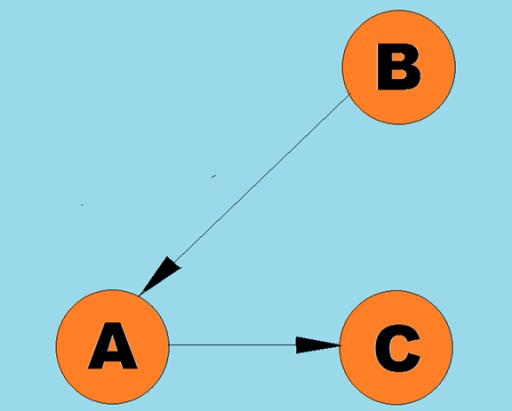通常、グラフは、いくつかの頂点がエッジ (円弧) で接続されている図で表されます。エッジがトラバース方向を示すグラフは、有向グラフと呼ばれます。グラフがトラバースの方向を示さないエッジによって接続されている場合、それを無向グラフと言います。これは、頂点 A から頂点 B へ、および頂点 B から頂点 A への両方向への移動が可能であることを意味します。接続されたグラフとは、各頂点から他の頂点へ少なくとも 1 つのパスがつながっているグラフです (図のように)。上の例）。そうでない場合、グラフは切断されていると言われます。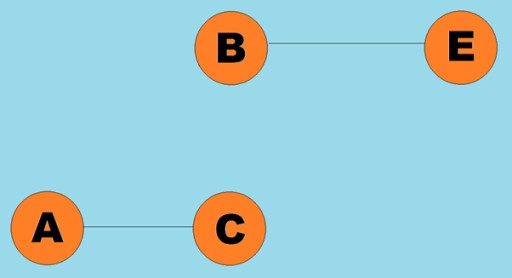エッジ (円弧) に重みを割り当てることもできます。重みは、たとえば 2 つの頂点間の物理的距離 (または 2 つの頂点間の相対的な移動時間) を表す数値です。これらのグラフは重み付きグラフと呼ばれます。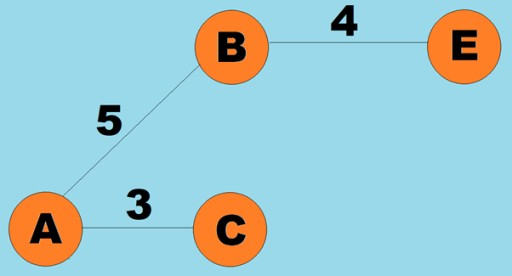

3. 経路探索アルゴリズム (深さ優先、幅優先)

グラフで実行される基本操作の 1 つは、特定の頂点から到達可能なすべての頂点を決定することです。ある都市から別の都市へのバスの乗車方法を、移動の可能性も含めて判断しようとしていると想像してください。直接アクセスできる都市もあれば、他の都市を経由しないとアクセスできない都市もあります。特定の頂点から到達できるすべての頂点を見つける必要がある状況は他にもたくさんあります。グラフを走査するには、深さ優先と幅優先の 2 つの主な方法があります。この両方について調べていきます。どちらの方法も、接続されているすべての頂点を横断します。深さ優先アルゴリズムと幅優先アルゴリズムをさらに詳しく調べるために、次のグラフを使用します。

深さ優先検索

これは、最も一般的なグラフ走査方法の 1 つです。深さ優先戦略は、グラフ内をできるだけ深く調査することです。次に、行き止まりに到達した後、以前に訪問していない隣接する頂点のうち最も近い頂点に戻ります。このアルゴリズムは、行き止まりに達したときにどこに戻るかに関する情報をスタックに保存します。深さ優先検索のルール:

1. 以前に訪問されていない隣接する頂点を訪問し、訪問済みとしてマークし、スタックにプッシュします。
2. この頂点に移動します。
3. 手順 1 を繰り返します。
4. ステップ 1 が不可能な場合は、前の頂点に戻ってステップ 1 の実行を試みます。それが不可能な場合は、その頂点より前の頂点に戻り、トラバースを続行できる頂点が見つかるまで同様に繰り返します。
5. すべての頂点がスタック上に配置されるまで続けます。

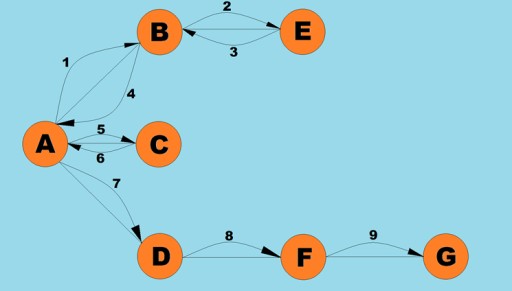このアルゴリズムの Java コードがどのようになるかを見てみましょう。

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

頂点は次のようになります。

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

このアルゴリズムを特定の頂点で実行して、正しく動作するかどうかを確認してみましょう。

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

コンソール出力: 隣接行列があり、ループ内でループを使用しているため、時間計算量は O(N²) になります。

幅優先検索

深さ優先検索と同様、このアルゴリズムは最も単純かつ基本的なグラフ走査方法の 1 つです。要点は、現在の頂点があるということです。未訪問の隣接する頂点をすべてキューに入れ、次の要素 (キューの先頭に格納されている頂点) を選択します。これが現在の頂点になります… このアルゴリズムを段階に分けると、次のステップを確認できます。

1. 現在の頂点に隣接する次の未訪問の頂点を訪問し、事前に訪問済みとしてマークし、キューに追加します。
2. ステップ #1 を実行できない場合は、キューから頂点を削除し、それを現在の頂点にします。
3. ステップ #1 と #2 を実行できない場合、走査は終了です。すべての頂点が走査されています (接続されたグラフがある場合)。

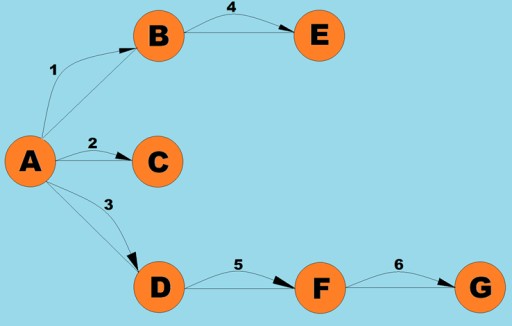ここでのグラフ クラスは、検索メソッド自体とキューが内部スタックを置き換える点を除いて、深さ優先検索アルゴリズムに使用したものとほぼ同じです。

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

Vertex クラスは、深さ優先検索アルゴリズムで使用したものと同じです。このアルゴリズムを実行してみましょう。

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

コンソール出力: 繰り返しになりますが、隣接行列があり、ループ内にネストされたループを使用しているため、上記のアルゴリズムの時間計算量は O(N²) です。

4. ダイクストラのアルゴリズム

前述したように、グラフには有向性と無向性があります。そして、重み付けもできることを思い出してください。重み付き有向グラフは、実生活でよく見られる関係をモデル化します。たとえば、都市が頂点であり、その間のエッジが有向エッジの方向に流れる一方通行の道路である都市の地図です。あなたが運送会社で、遠く離れた 2 つの都市間の最短ルートを見つける必要があるとします。どうやってやりますか？2 つの頂点間の最短経路を見つけることは、重み付きグラフを使用して解決される最も一般的な問題の 1 つです。この問題を解決するために、ダイクストラのアルゴリズムを使用します。これを実行すると、特定の最初の頂点から他のすべての頂点までの最短パスがわかります。このアルゴリズムの手順は何ですか? この質問に答えてみます。ダイクストラのアルゴリズムのステップ:

• ステップ 1: 移動先のコストが最も低い (エッジの重みが最も低い) 隣接ノードを見つけます。あなたはまさに先頭に立って、ノード A かノード B のどちらに行くべきかを考えています。これらの各ノードに移動するコストはいくらでしょうか?
• ステップ 2: В からエッジを横断するときに、アルゴリズムがまだ訪問していないすべてのノード В の隣接ノードまで移動する距離を計算します。新しい距離が古い距離より小さい場合、エッジ B を通るパスがこの頂点の新しい最短パスになります。
• ステップ 3: 頂点 B を訪問済みとしてマークします。
• ステップ 4: ステップ 1 に進みます。

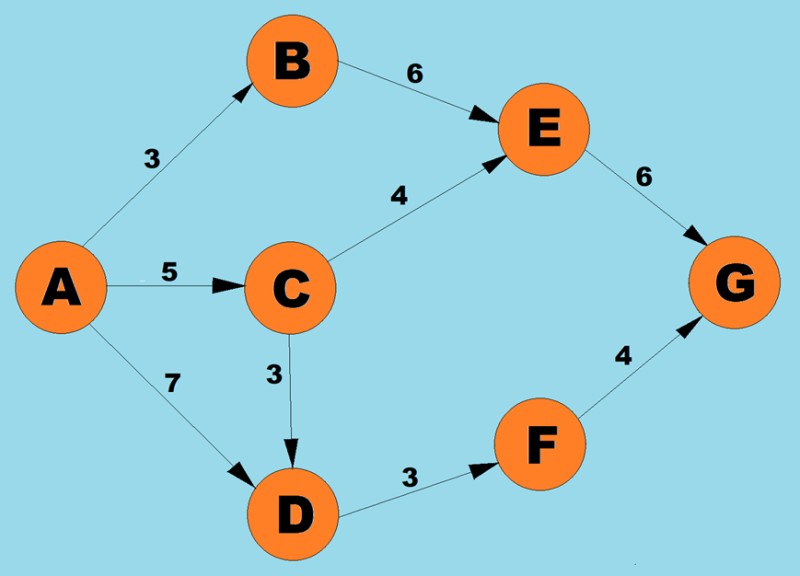すべての頂点が訪問されるまで、これらの手順をループで繰り返します。次の重み付き有向グラフを考えてみましょう。上記のアルゴリズムを使用して、A から G への最短経路を決定します。

1. 頂点 A には、重み 3 で B へ、重み 5 で С へ、重み 7 で D への 3 つのパスが考えられます。アルゴリズムの最初のステップに従って、コスト (エッジの重み) が最も低いノードを選択します。この場合、B.

2. B の唯一の未訪問の近傍は頂点 Е であるため、この頂点を通過した場合のパスがどのようになるかを確認します。3(AB) + 6(BE) = 9。

   したがって、A から E への現在の最短パスは 9 であると記録します。

3. 頂点 B での作業が完了したので、エッジの重みが最小になる次の頂点の選択に進みます。

   頂点 A と B から、可能性は頂点 D (7)、C (5)、または E (6) です。

   С へのエッジの重みが最も小さいため、この頂点に進みます。

4. 次に、前と同様に、C を通過するときに隣接する頂点への最短パスを見つけます。

   • AD = 5 (AC) + 3 (CD) = 8 ですが、以前の最短パス (AC = 7) は С を通る今回の最短パスより小さいため、最短パス (AC = 7) を変更しません。

   • CE = 5(AC) + 4(CE) = 9。この新しい最短パスは前のパスと等しいため、これも変更しないままにします。

5. 最も近いアクセス可能な頂点 (E および D) から、エッジの重みが最小の頂点、つまり D (3) を選択します。

6. 隣接する F への最短経路を見つけます。

   AF = 7(AD) + 3(DF) = 9

7. 最も近いアクセス可能な頂点 (E および F) から、エッジの重みが最小の頂点、つまり F (3) を選択します。

8. 隣接する G への最短経路を見つけます。

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   つまり、A から G へのパスが見つかりました。

   ただし、それが最短であることを確認するには、頂点 E に対しても手順を実行する必要があります。

9. 頂点 G には有向エッジが指す隣接する頂点がないため、頂点 E だけが残っており、それを選択します。

10. 隣接する G への最短経路を見つけます。

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15。このパスは前の最短パス (AG (14)) より長いため、このパスを変更しないままにします。

    G からつながる頂点がないため、この頂点でアルゴリズムのステップを実行することは意味がありません。これは、アルゴリズムの作業が完了したことを意味します。

前に述べたように、AG の最短パスを見つけることに加えて、頂点 A から他のすべての頂点 (AB、AC、AD、AE、AF) までの最短パスも取得しました。さて、今度はこれを Java でどのように実行できるかを見てみましょう。頂点クラスから始めましょう。

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

頂点クラスは、幅優先検索に使用される頂点クラスと実質的に同じです。最短パスを表示するには、必要なデータを含む新しいクラスが必要です。

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

このクラスでは、パスの合計距離と、最短パスに沿って通過するときに通過する頂点を確認できます。次に、実際にグラフ内の最短パスをたどるクラスを見てみましょう。ここに Graph クラスがあります。

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

魔法はこれだけです =) さて、このアルゴリズムが実際に動作している様子を見てみましょう:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

そして、コンソール出力は次のようになります。 ループが入れ子になっているため、このアルゴリズムの時間計算量は O(N²) に他なりません。今日はこれで終わりです。ご清聴ありがとうございました！