工作面試中的問答：Java 中的演算法，第 2 部分

這是演算法簡要概述的第二部分。這是第一篇文章 的連結。 之前我們研究了各種數組排序演算法以及所謂的貪婪演算法。今天我們將討論圖以及與之相關的演算法。圖是程式設計中最靈活、最通用的結構之一。圖G通常由一對集合來定義，即G = (V, R)，其中：

• V是一組頂點；
• R 是連接頂點對的一組線。

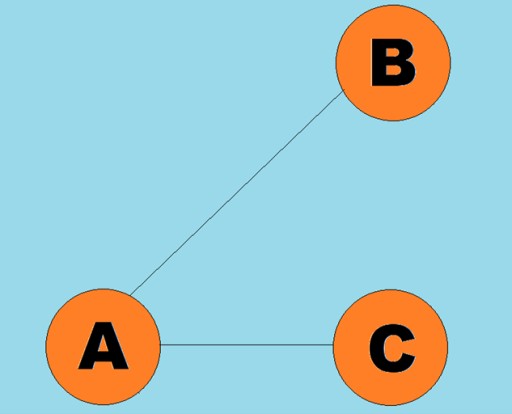無向連接線稱為邊： 有向線稱為弧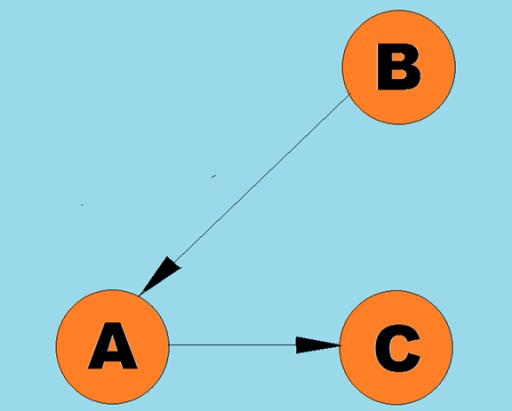：通常，圖形由其中一些頂點透過邊（弧）連接的圖來表示。邊指示遍歷方向的圖稱為有向圖。如果一個圖是由不指示遍歷方向的邊連接的，那麼我們說它是無向圖。這意味著可以在兩個方向上移動：從頂點 A 到頂點 B，以及從頂點 B 到頂點 A。連通圖是其中至少一條路徑從每個頂點通往任何其他頂點的圖（如上面的例子） 。如果不是這種情況，則該圖稱為斷開連接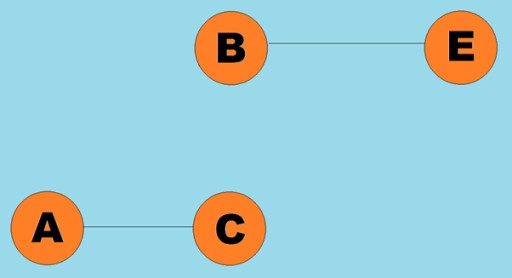：權重也可以分配給邊（弧）。權重是表示例如兩個頂點之間的物理距離（或兩個頂點之間的相對行進時間）的數字。這些圖稱為加權圖：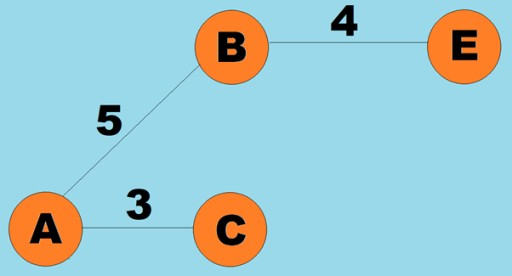

3. 尋路演算法（深度優先、廣度優先）

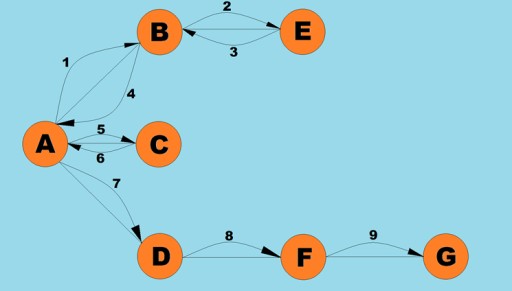
對圖執行的基本操作之一是確定從給定頂點可到達的所有頂點。想像一下，您正在嘗試確定如何乘坐巴士從一個城市到另一個城市，包括可能的轉乘。有的城市可以直達，有的則需要經過其他城市才能到達。在許多其他情況下，您可能需要尋找從給定頂點可以到達的所有頂點。遍歷圖的方式主要有兩種：深度優先和廣度優先。我們將探討這兩個面向。兩種方法都會遍歷所有連接的頂點。為了進一步探索深度優先和廣度優先演算法，我們將使用下圖：

深度優先搜尋

這是最常見的圖遍歷方法之一。深度優先策略是在圖中盡可能深入。然後，在到達死胡同後，我們返回到之前未訪問過的相鄰頂點的最近頂點。該演算法在堆疊上儲存有關到達死胡同時返回位置的資訊。深度優先搜尋規則：

1. 訪問以前未訪問過的相鄰頂點，將其標記為已訪問，並將其壓入堆疊。
2. 移動到這個頂點。
3. 重複步驟 1。
4. 如果步驟 1 不可能，則回到前一個頂點並嘗試執行步驟 1。如果不可能，則返回到該頂點之前的頂點，依此類推，直到找到可以繼續遍歷的頂點。
5. 繼續下去，直到所有頂點都在堆疊上。

讓我們來看看該演算法的 Java 程式碼可能會是什麼樣子：

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

頂點看起來像這樣：

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

讓我們用特定的頂點來運行這個演算法，看看它是否正常運作：

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

控制台輸出： 由於我們有一個鄰接矩陣並且在循環中使用循環，因此時間複雜度將為 O(N²)。

廣度優先搜尋

與深度優先搜尋一樣，該演算法是最簡單、最基本的圖遍歷方法之一。重點是我們有一些當前的頂點。我們將所有未訪問的相鄰頂點放入隊列中，並選擇下一個元素（即存儲在隊列頭部的頂點），該元素成為當前頂點…將該演算法分為幾個階段，我們可以確定以下步驟：

1. 訪問與當前頂點相鄰的下一個先前未訪問的頂點，將其標記為提前訪問過，並將其添加到佇列中。
2. 如果步驟#1 無法執行，則從佇列中刪除該頂點並使其成為目前頂點。
3. 如果步驟#1和#2無法執行，那麼我們就完成了遍歷——每個頂點都已被遍歷（如果我們有一個連通圖）。

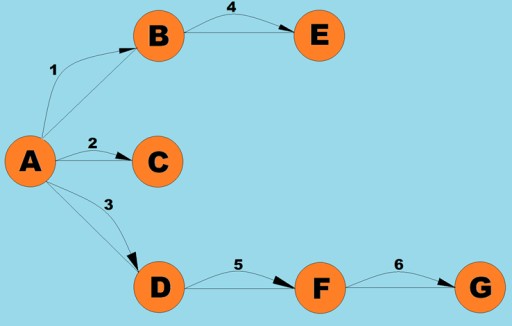這裡的圖類與我們用於深度優先搜尋演算法的圖類幾乎相同，除了搜尋方法本身以及佇列取代了內部堆疊：

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

Vertex 類別與我們在深度優先搜尋演算法中使用的類別相同。讓我們將這個演算法付諸實現：

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

控制台輸出： 再次強調：我們有一個鄰接矩陣，並且使用了嵌套在循環中的循環，因此上述演算法的時間複雜度是 O(N²)。

4.Dijkstra演算法

如前所述，圖可以是有向的，也可以是無向的。您會記得它們也可以被加權。加權有向圖對現實生活中常見的關係進行建模：例如，在城市地圖中，城市是頂點，它們之間的邊是單向交通的道路，沿著有向邊的方向流動。假設您是一家貨運公司，您需要找到兩個遙遠城市之間的最短路線。你會怎麼做？尋找兩個頂點之間的最短路徑是使用加權圖解決的最常見問題之一。為了解決這個問題，我們使用Dijkstra演算法。一旦運行它，您就會知道從給定的初始頂點到每個其他頂點的最短路徑。這個演算法的步驟是什麼？我將嘗試回答這個問題。Dijkstra演算法的步驟：

• 步驟 1：找到導航成本最低（邊權重最低）的鄰近節點。您站在最開始的位置，思考要去哪裡：節點 A 或節點 B。移動到每個節點的成本是多少？
• 步驟2：計算從B開始遍歷邊時，到演算法尚未造訪過的所有節點B的鄰居的距離。如果新距離小於舊距離，則通過邊 B 的路徑將成為該頂點的新最短路徑。
• 步驟3：將頂點B標記為已存取。
• 步驟 4：轉到步驟 1。

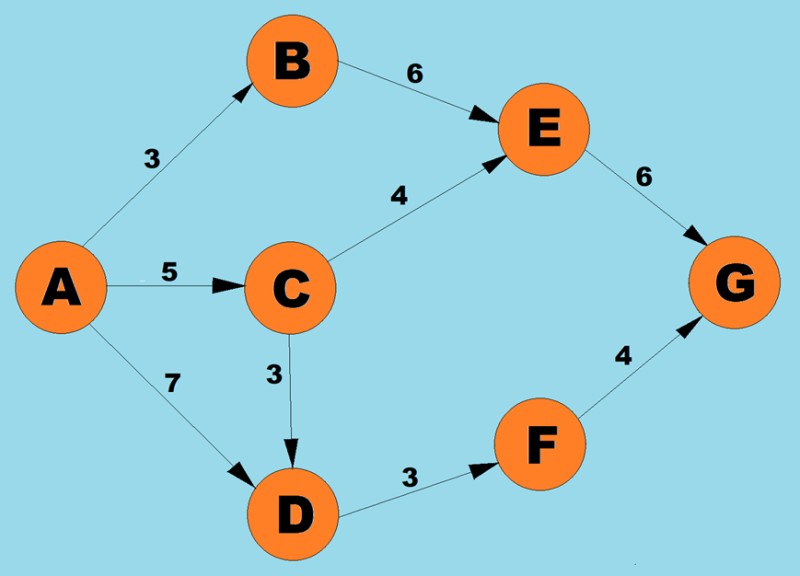我們將循環重複這些步驟，直到訪問完所有頂點。讓我們考慮以下加權有向圖：使用上述演算法，我們將確定從 A 到 G 的最短路徑：

1. 頂點 A 有 3 種可能的路徑：到 B 的權重為 3、到 С 的權重為 5、到 D 的權重為 7。根據演算法的第一步，我們選擇成本最低的節點（邊權重）。在這種情況下，B.

2. 由於 B 唯一未訪問的鄰居是頂點 Е，因此我們檢查如果經過該頂點，路徑將會是什麼。3(AB) + 6(BE) = 9。

   因此，我們記錄目前從 A 到 E 的最短路徑是 9。

3. 由於我們對頂點 B 的處理已完成，因此我們繼續選擇邊具有最小權重的下一個頂點。

   從頂點 A 和 B 開始，可能的頂點是 D (7)、C (5) 或 E (6)。

   С 的邊權重最小，所以我們去這個頂點。

4. 接下來，和之前一樣，我們找到經過 C 時到達相鄰頂點的最短路徑：

   • AD = 5 (AC) + 3 (CD) = 8，但由於先前的最短路徑 (AC = 7) 小於經過 С 的這條最短路徑，因此我們保持最短路徑 (AC = 7) 不變。

   • CE = 5(AC) + 4(CE) = 9。這條新的最短路徑與前一條相同，因此我們也保持不變。

5. 從最近的可存取頂點（E和D）中，選擇邊權最小的頂點，即D（3）。

6. 我們找到到其鄰居 F 的最短路徑。

   AF = 7(AD) + 3(DF) = 9

7. 從最近的可訪問頂點（E和F）中，選擇邊權重最小的頂點，即F（3）。

8. 找到到其鄰居 G 的最短路徑。

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   所以，我們找到了一條從A到G的路。

   但為了確保它是最短的，我們也必須在頂點 E 上執行我們的步驟。

9. 因為頂點 G 沒有有向邊指向的相鄰頂點，所以我們只剩下頂點 E，所以我們選擇它。

10. 找到到鄰居G的最短路徑。

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15。這條路徑比之前的最短路徑（AG（14））長，所以我們保持這條路徑不變。

    由於沒有從 G 引出的頂點，因此在該頂點上運行演算法步驟是沒有意義的。這意味著演算法的工作已經完成。

正如我之前所說，除了找到AG的最短路徑之外，我們還獲得了從頂點A到其他每個頂點（AB，AC，AD，AE，AF）的最短路徑。好吧，現在是時候看看如何在 Java 中完成此操作了。讓我們從頂點類別開始：

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

頂點類別實際上與用於廣度優先搜尋的頂點類別相同。為了顯示最短路徑，我們需要一個新類別來包含我們需要的資料：

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

在這個類別中，我們可以看到路徑的總距離以及經過最短路徑時將要遍歷的頂點。現在讓我們看看我們實際遍歷圖形的最短路徑的類別。所以這裡我們有 Graph 類別：

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

這就是神奇之處 =) 現在，讓我們看看這個演算法的實際應用：

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

控制台輸出是這樣的： 這個演算法的時間複雜度正是 O(N²)，因為我們有嵌套迴圈。這就是我今天的全部內容。感謝您的關注！