Las preguntas y respuestas de las entrevistas de trabajo: algoritmos en Java, parte 2

Esta es la segunda parte de una breve descripción de los algoritmos. Aquí hay un enlace al primer artículo . Anteriormente analizamos varios algoritmos para ordenar matrices, así como el llamado algoritmo codicioso. Hoy hablaremos de gráficos y los algoritmos asociados a ellos. Un gráfico es una de las estructuras más flexibles y versátiles en programación. El gráfico G suele estar definido por un par de conjuntos, es decir, G = (V, R), donde:

• V es un conjunto de vértices;
• R es un conjunto de líneas que conectan pares de vértices.

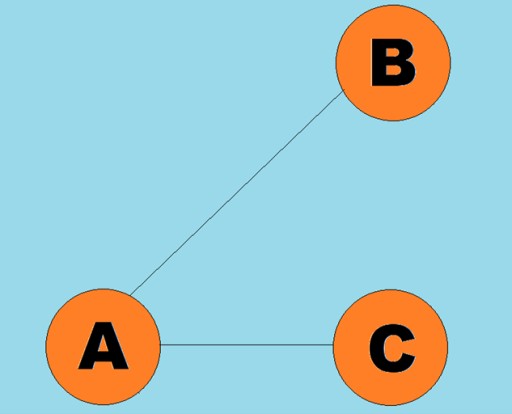Las líneas de conexión no dirigidas se llaman aristas: Las líneas dirigidas se llaman arcos: 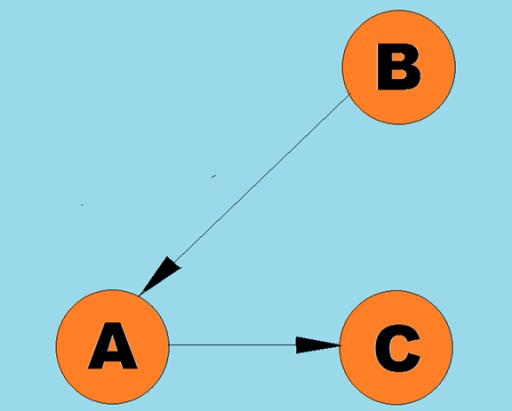Normalmente, un gráfico se representa mediante un diagrama en el que algunos de los vértices están conectados por aristas (arcos). Los gráficos cuyos bordes indican una dirección de recorrido se denominan gráficos dirigidos. Si un gráfico está conectado por aristas que no indican la dirección de recorrido, entonces decimos que es un gráfico no dirigido. Esto significa que el movimiento es posible en ambas direcciones: tanto del vértice A al vértice B como del vértice B al vértice A. Un gráfico conexo es un gráfico en el que al menos un camino conduce desde cada vértice a cualquier otro vértice (como en el ejemplo anterior). Si no es así, se dice que el gráfico está desconectado: 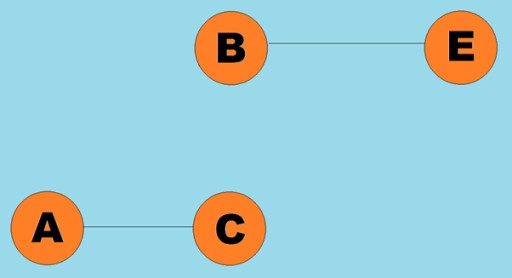también se pueden asignar pesos a las aristas (arcos). Los pesos son números que representan, por ejemplo, la distancia física entre dos vértices (o el tiempo relativo de viaje entre dos vértices). Estos gráficos se llaman gráficos ponderados: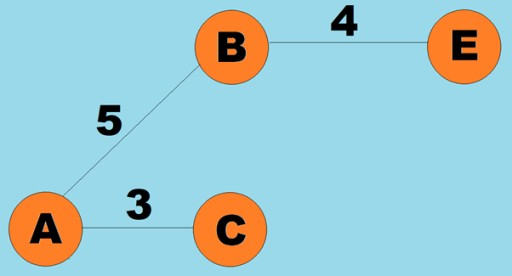

3. Algoritmos de búsqueda de rutas (primero en profundidad, primero en amplitud)

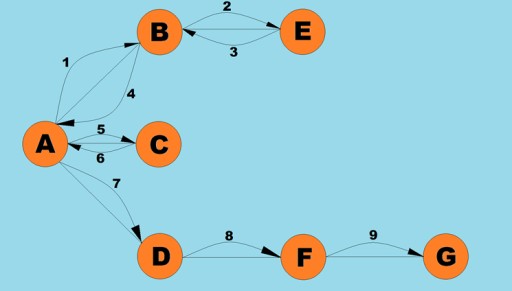
Una de las operaciones básicas que se realizan con los gráficos es determinar todos los vértices alcanzables desde un vértice determinado. Imagine que está tratando de determinar cómo puede viajar en autobús de una ciudad a otra, incluidos los posibles transbordos. A algunas ciudades se puede llegar directamente, mientras que a otras solo se puede llegar pasando por otras ciudades. Hay muchas otras situaciones en las que es posible que necesites encontrar todos los vértices a los que puedes llegar desde un vértice determinado. Hay dos formas principales de recorrer gráficos: primero en profundidad y primero en amplitud. Exploraremos ambos. Ambos métodos atraviesan todos los vértices conectados. Para explorar más a fondo los algoritmos de profundidad y amplitud, usaremos el siguiente gráfico:

Búsqueda en profundidad

Este es uno de los métodos de recorrido de gráficos más comunes. La estrategia de profundidad primero es profundizar lo más posible en un gráfico. Luego, después de llegar a un callejón sin salida, volvemos al vértice más cercano que anteriormente no ha visitado vértices adyacentes. Este algoritmo almacena información en la pila sobre dónde regresar cuando se llega a un callejón sin salida. Reglas para la búsqueda en profundidad:

1. Visite un vértice adyacente no visitado anteriormente, márquelo como visitado y empújelo hacia la pila.
2. Muévete a este vértice.
3. Repita el paso 1.
4. Si el paso 1 es imposible, regrese al vértice anterior e intente realizar el paso 1. Si eso no es posible, regrese al vértice anterior a ese, y así sucesivamente, hasta que encontremos un vértice desde el cual podamos continuar el recorrido.
5. Continúe hasta que todos los vértices estén en la pila.

Echemos un vistazo a cómo se vería el código Java para este algoritmo:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

Un vértice se ve así:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

Ejecutemos este algoritmo con vértices específicos y veamos si funciona correctamente:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

Salida de consola: Como tenemos una matriz de adyacencia y estamos usando un bucle dentro de un bucle, la complejidad del tiempo será O (N²).

Búsqueda en amplitud

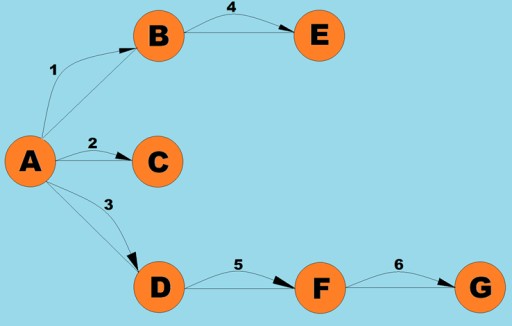
Al igual que la búsqueda en profundidad, este algoritmo es uno de los métodos de recorrido de gráficos más simples y básicos. La esencia es que tenemos algún vértice actual. Colocamos todos sus vértices adyacentes no visitados en una cola y seleccionamos el siguiente elemento (que es el vértice almacenado al principio de la cola), que se convierte en el vértice actual... Dividiendo este algoritmo en etapas, podemos identificar los siguientes pasos:

1. Visite el siguiente vértice adyacente al vértice actual no visitado previamente, márquelo como visitado de antemano y agréguelo a la cola.
2. Si no se puede realizar el paso 1, elimine el vértice de la cola y conviértalo en el vértice actual.
3. Si no se pueden realizar los pasos 1 y 2, entonces hemos terminado de atravesar: se han atravesado todos los vértices (si tenemos un gráfico conectado).

La clase de gráfico aquí es casi idéntica a la que usamos para el algoritmo de búsqueda en profundidad, excepto por el método de búsqueda en sí y el hecho de que una cola reemplaza la pila interna:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

La clase Vertex es idéntica a la que usamos con el algoritmo de búsqueda en profundidad. Pongamos este algoritmo en acción:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

Salida de consola: Nuevamente: tenemos una matriz de adyacencia y usamos un bucle anidado dentro de un bucle, por lo que la complejidad temporal del algoritmo anterior es O (N²).

4. Algoritmo de Dijkstra

Como se mencionó anteriormente, los gráficos pueden ser dirigidos o no dirigidos. Y como recordarás, también se pueden pesar. Los gráficos dirigidos y ponderados modelan relaciones que se encuentran a menudo en la vida real: por ejemplo, un mapa de ciudades donde las ciudades son vértices y los bordes entre ellas son carreteras con tráfico de un solo sentido, que fluye en la dirección del borde dirigido. Digamos que eres una empresa de transporte y necesitas encontrar la ruta más corta entre dos ciudades distantes. ¿Como lo harias? Encontrar el camino más corto entre dos vértices es uno de los problemas más comunes que se resuelven mediante gráficos ponderados. Para resolver este problema utilizamos el algoritmo de Dijkstra. Una vez que lo ejecutes, conocerás los caminos más cortos desde un vértice inicial determinado hasta todos los demás. ¿Cuáles son los pasos de este algoritmo? Intentaré responder a esta pregunta. Pasos del algoritmo de Dijkstra:

• Paso 1: busque el nodo adyacente al que tenga el costo más bajo para navegar (peso de borde más bajo). Estás parado desde el principio y pensando adónde ir: al nodo A o al nodo B. ¿Cuál es el costo de mudarse a cada uno de estos nodos?
• Paso 2: calcule la distancia a recorrer hasta todos los vecinos del nodo B que aún no han sido visitados por el algoritmo al atravesar el borde desde B. Si la nueva distancia es menor que la anterior, entonces el camino a través del borde B se convierte en el nuevo camino más corto para este vértice.
• Paso 3: marque el vértice B como visitado.
• Paso 4: vaya al paso 1.

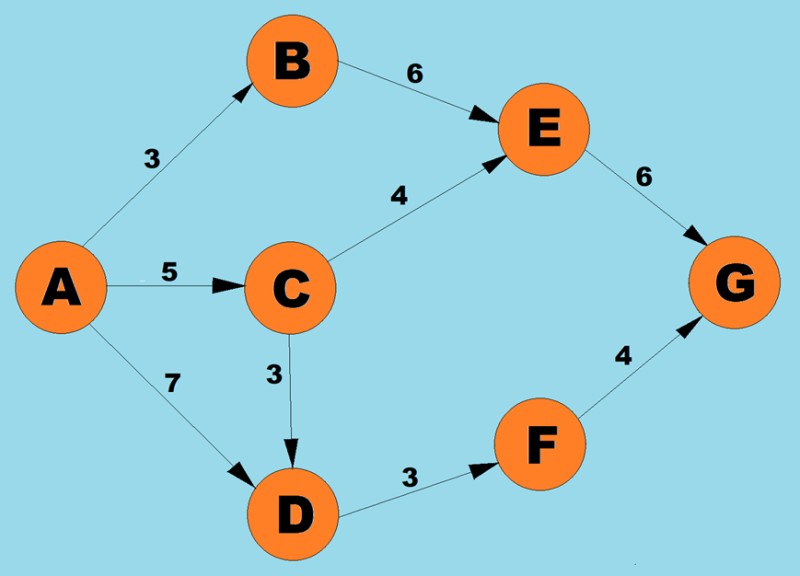Repetiremos estos pasos en un bucle hasta que se hayan visitado todos los vértices. Consideremos el siguiente gráfico dirigido ponderado: utilizando el algoritmo anterior, determinaremos el camino más corto de A a G:

1. Hay tres caminos posibles para el vértice A: a B con peso 3, a С con peso 5 y a D con peso 7. Según el primer paso del algoritmo, seleccionamos el nodo con el menor costo (peso de borde). En este caso, B.

2. Dado que el único vecino no visitado de B es el vértice Е, comprobamos cuál sería el camino si pasáramos por este vértice. 3(AB) + 6(SER) = 9.

   Por lo tanto, registramos que el camino más corto actual de A a E es 9.

3. Como nuestro trabajo con el vértice B está completo, procedemos a seleccionar el siguiente vértice cuya arista tenga el peso mínimo.

   De los vértices A y B, las posibilidades son los vértices D (7), C (5) o E (6).

   La arista de C tiene el peso más pequeño, por lo que vamos a este vértice.

4. A continuación, como antes, encontramos el camino más corto a los vértices vecinos al pasar por C:

   • AD = 5 (AC) + 3 (CD) = 8, pero como el camino más corto anterior (AC = 7) es menor que éste a través de С, mantenemos el camino más corto (AC = 7) sin cambios.

   • CE = 5(AC) + 4(CE) = 9. Este nuevo camino más corto es igual al anterior, por lo que tampoco lo modificamos.

5. Desde los vértices accesibles más cercanos (E y D), seleccione el vértice con el peso de borde más pequeño, es decir, D (3).

6. Encontramos el camino más corto hacia su vecino F.

   AF = 7(AD) + 3(DF) = 9

7. Desde los vértices accesibles más cercanos (E y F), seleccione el vértice con el peso de borde más pequeño, es decir, F (3).

8. Encuentre el camino más corto hacia su vecino G.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   Entonces, hemos encontrado un camino de A a G.

   Pero para asegurarnos de que sea el más corto, también debemos realizar nuestros pasos en el vértice E.

9. Debido a que el vértice G no tiene vértices vecinos apuntados por aristas dirigidas, solo nos queda el vértice E, por lo que lo elegimos.

10. Encuentre el camino más corto al vecino G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Este camino es más largo que el camino más corto anterior (AG (14)), por lo que dejamos este camino sin cambios.

    Dado que no hay vértices que partan de G, no tiene sentido ejecutar los pasos del algoritmo en este vértice. Eso significa que el trabajo del algoritmo está completo.

Como dije antes, además de encontrar el camino más corto para AG, también obtuvimos los caminos más cortos desde el vértice A hasta todos los demás vértices (AB, AC, AD, AE, AF). Bueno, ahora es el momento de ver cómo se puede hacer esto en Java. Comencemos con la clase de vértice:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

La clase de vértice es prácticamente idéntica a la clase de vértice utilizada para la búsqueda en amplitud. Para mostrar las rutas más cortas, necesitamos una nueva clase que contendrá los datos que necesitamos:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

En esta clase podemos ver la distancia total del camino y los vértices que se recorrerán al pasar por el camino más corto. Y ahora veamos la clase en la que realmente recorremos el camino más corto a través del gráfico. Entonces aquí tenemos la clase Graph:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

Esa es toda la magia =) Ahora, echemos un vistazo a este algoritmo en acción:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

Y la salida de la consola es esta: La complejidad temporal de este algoritmo no es otra que O(N²), ya que tenemos bucles anidados. Eso es todo lo que tengo hoy. ¡Gracias por tu atención!