이것은 알고리즘에 대한 간략한 개요의 두 번째 부분입니다. 첫 번째 기사
에 대한 링크는 다음과 같습니다 . 앞서 우리는 배열 정렬을 위한 다양한 알고리즘과 소위 그리디 알고리즘을 살펴보았습니다. ![취업 면접 Q&A: Java 알고리즘, 2부 - 1]()
오늘 우리는 그래프와 그래프와 관련된 알고리즘에 대해 이야기하겠습니다. 그래프는 프로그래밍에서 가장 유연하고 다양한 구조 중 하나입니다. 그래프 G는 일반적으로 집합 쌍, 즉 G = (V, R)으로 정의됩니다. 여기서:
![취업 면접 Q&A: Java 알고리즘, 2부 - 2]()
방향이 있는 선을 호라고 합니다. ![취업 면접 Q&A: Java 알고리즘, 2~3부]()
일반적으로 그래프는 일부 정점이 모서리(호)로 연결된 다이어그램으로 표시됩니다. 모서리가 순회 방향을 나타내는 그래프를 유향 그래프라고 합니다. 그래프가 순회 방향을 나타내지 않는 모서리로 연결된 경우 이를 무방향 그래프라고 말합니다. 이는 정점 A에서 정점 B로, 정점 B에서 정점 A로 양방향으로 이동이 가능하다는 것을 의미합니다. 연결 그래프는 최소한 하나의 경로가 각 정점에서 다른 정점으로 연결되는 그래프입니다. 위의 예). 그렇지 않은 경우 그래프는 연결이 끊어졌다고 합니다. ![취업 면접 Q&A: Java 알고리즘, 2~4부]()
가중치는 모서리(호)에도 할당될 수 있습니다. 가중치는 예를 들어 두 꼭지점 사이의 물리적 거리(또는 두 꼭지점 사이의 상대적 이동 시간)를 나타내는 숫자입니다. 이러한 그래프를 가중치 그래프라고 합니다.![취업 면접 Q&A: Java 알고리즘, 2~5부]()
![취업 면접 Q&A: Java 알고리즘, 2~6부]()
![취업 면접 Q&A: Java 알고리즘, 2~7부]()
이 알고리즘의 Java 코드가 어떤 모습인지 살펴보겠습니다.
![취업 면접 Q&A: Java 알고리즘, 2부 - 8부]()
여기의 그래프 클래스는 검색 방법 자체와 대기열이 내부 스택을 대체한다는 사실을 제외하면 깊이 우선 검색 알고리즘에 사용한 것과 거의 동일합니다.
![취업 면접 Q&A: Java 알고리즘, 2부 - 9부]()
위의 알고리즘을 사용하여 A에서 G까지의 최단 경로를 결정합니다.
![취업 면접 Q&A: Java 알고리즘, 2부 - 10]()
오늘 우리는 그래프와 그래프와 관련된 알고리즘에 대해 이야기하겠습니다. 그래프는 프로그래밍에서 가장 유연하고 다양한 구조 중 하나입니다. 그래프 G는 일반적으로 집합 쌍, 즉 G = (V, R)으로 정의됩니다. 여기서:
- V는 정점의 집합입니다.
- R은 정점 쌍을 연결하는 선 집합입니다.
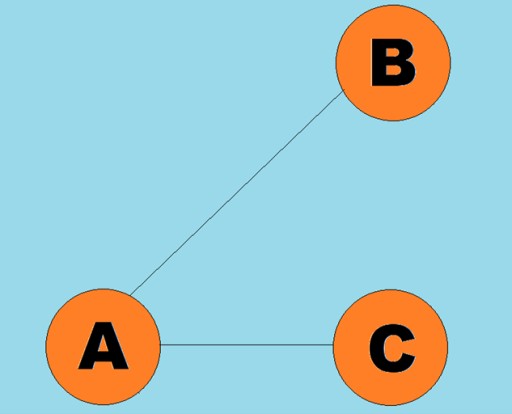방향이 있는 선을 호라고 합니다. 
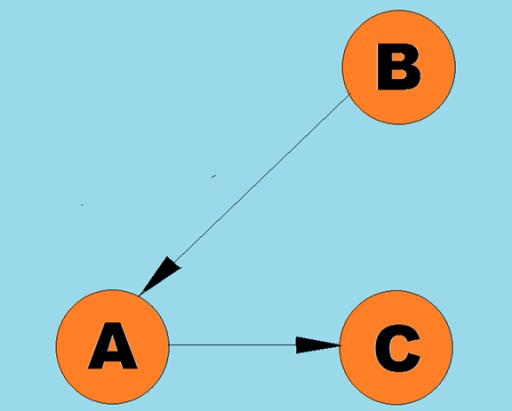일반적으로 그래프는 일부 정점이 모서리(호)로 연결된 다이어그램으로 표시됩니다. 모서리가 순회 방향을 나타내는 그래프를 유향 그래프라고 합니다. 그래프가 순회 방향을 나타내지 않는 모서리로 연결된 경우 이를 무방향 그래프라고 말합니다. 이는 정점 A에서 정점 B로, 정점 B에서 정점 A로 양방향으로 이동이 가능하다는 것을 의미합니다. 연결 그래프는 최소한 하나의 경로가 각 정점에서 다른 정점으로 연결되는 그래프입니다. 위의 예). 그렇지 않은 경우 그래프는 연결이 끊어졌다고 합니다. 
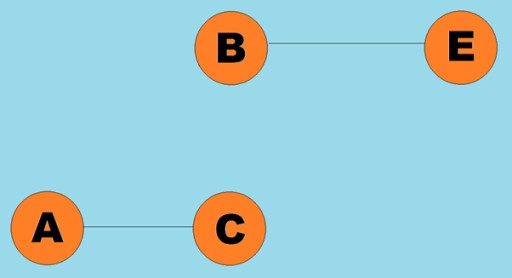가중치는 모서리(호)에도 할당될 수 있습니다. 가중치는 예를 들어 두 꼭지점 사이의 물리적 거리(또는 두 꼭지점 사이의 상대적 이동 시간)를 나타내는 숫자입니다. 이러한 그래프를 가중치 그래프라고 합니다.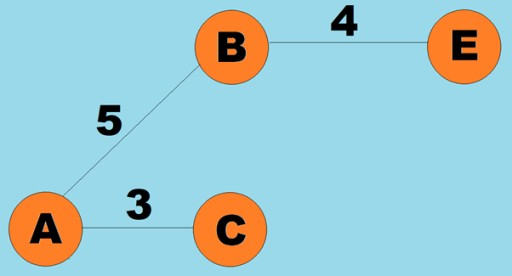
3. 길 찾기 알고리즘(깊이 우선, 너비 우선)
그래프로 수행되는 기본 작업 중 하나는 주어진 꼭지점에서 도달할 수 있는 모든 꼭지점을 결정하는 것입니다. 가능한 환승을 포함하여 한 도시에서 다른 도시로 버스를 타는 방법을 결정하려고 한다고 상상해 보십시오. 일부 도시는 직접 갈 수 있는 반면, 일부 도시는 다른 도시를 거쳐야만 도달할 수 있습니다. 주어진 정점에서 도달할 수 있는 모든 정점을 찾아야 하는 다른 상황도 많이 있습니다. 그래프를 탐색하는 방법에는 깊이 우선과 너비 우선이라는 두 가지 주요 방법이 있습니다. 우리는 이 두 가지를 모두 탐구할 것입니다. 두 방법 모두 연결된 모든 정점을 통과합니다. 깊이 우선 및 너비 우선 알고리즘을 더 자세히 살펴보기 위해 다음 그래프를 사용합니다.
깊이 우선 검색
이는 가장 일반적인 그래프 순회 방법 중 하나입니다. 깊이 우선 전략은 그래프에서 최대한 깊이 들어가는 것입니다. 그런 다음 막다른 골목에 도달한 후 이전에 방문하지 않은 인접한 정점이 있는 가장 가까운 정점으로 돌아갑니다. 이 알고리즘은 막다른 골목에 도달했을 때 반환할 위치에 대한 정보를 스택에 저장합니다. 깊이 우선 검색 규칙:- 이전에 방문하지 않은 인접 정점을 방문하여 방문한 것으로 표시하고 스택에 푸시합니다.
- 이 정점으로 이동합니다.
- 1단계를 반복합니다.
- 1단계가 불가능하면 이전 정점으로 돌아가서 1단계를 수행해 보세요. 이것이 가능하지 않다면 그 이전 정점으로 돌아가는 식으로 순회를 계속할 수 있는 정점을 찾을 때까지 계속됩니다.
- 모든 정점이 스택에 있을 때까지 계속합니다.
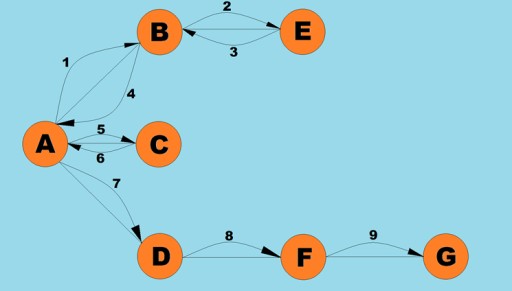이 알고리즘의 Java 코드가 어떤 모습인지 살펴보겠습니다.
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexArray[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Stack stack;
public Graph() { // Initialize internal fields
vertexArray = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) {
adjMat[j][k] = 0;
}
}
stack = new Stack<>();
}
public void addVertex(char lab) {
vertexArray[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexArray[v].getLabel());
}
public void dfs() { // Depth-first search
vertexArray[0].setVisited(true); // Take the first vertex
displayVertex(0);
stack.push(0);
while (!stack.empty()) {
int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
if (v == -1) { // If there is no unvisited adjacent vertex
stack.pop(); // The element is removed from the stack
}
else {
vertexArray[v].setVisited(true);
displayVertex(v);
stack.push(v); // The element goes on top of the stack
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexArray[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
return j; // Returns the first vertex found
}
}
return -1;
}
}public class Vertex {
private char label; // for example, 'A'
public boolean visited;
public Vertex(final char label) {
this.label = label;
visited = false;
}
public char getLabel() {
return this.label;
}
public boolean isVisited() {
return this.visited;
}
public void setVisited(final boolean visited) {
this.visited = visited;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.dfs();
}
}
방문: ABECDFG
인접 행렬이 있고 루프 내에서 루프를 사용하므로 시간 복잡도는 O(N²)입니다.
너비 우선 검색
깊이 우선 탐색과 마찬가지로 이 알고리즘은 가장 간단하고 기본적인 그래프 순회 방법 중 하나입니다. 요점은 현재 정점이 있다는 것입니다. 방문하지 않은 인접한 정점을 모두 대기열에 넣고 현재 정점이 되는 다음 요소(큐의 헤드에 저장된 정점)를 선택합니다. 이 알고리즘을 여러 단계로 나누어 다음 단계를 식별할 수 있습니다.- 현재 정점에 인접한 이전에 방문하지 않은 다음 정점을 방문하고 미리 방문했다고 표시한 후 대기열에 추가합니다.
- 1단계를 수행할 수 없는 경우 큐에서 정점을 제거하고 이를 현재 정점으로 만듭니다.
- 1단계와 2단계를 수행할 수 없으면 순회가 완료된 것입니다. 즉, 모든 정점이 순회된 것입니다(연결된 그래프가 있는 경우).
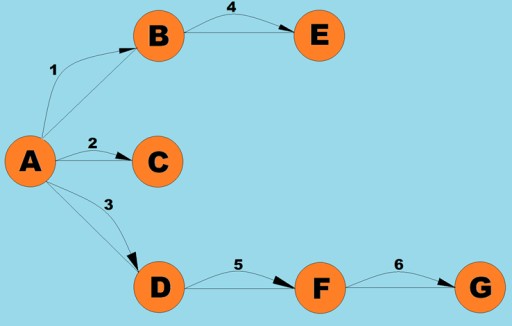여기의 그래프 클래스는 검색 방법 자체와 대기열이 내부 스택을 대체한다는 사실을 제외하면 깊이 우선 검색 알고리즘에 사용한 것과 거의 동일합니다.
public class Graph {
private final int MAX_VERTS = 10;
private Vertex vertexList[]; // Array of vertices
private int adjMat[][]; // Adjacency matrix
private int nVerts; // Current number of vertices
private Queue queue;
public Graph() {
vertexList = new Vertex[MAX_VERTS];
adjMat = new int[MAX_VERTS][MAX_VERTS];
nVerts = 0;
for (int j = 0; j < MAX_VERTS; j++) {
for (int k = 0; k < MAX_VERTS; k++) { // Fill the adjacency matrix with zeros
adjMat[j][k] = 0;
}
}
queue = new PriorityQueue<>();
}
public void addVertex(char lab) {
vertexList[nVerts++] = new Vertex(lab);
}
public void addEdge(int start, int end) {
adjMat[start][end] = 1;
adjMat[end][start] = 1;
}
public void displayVertex(int v) {
System.out.println(vertexList[v].getLabel());
}
public void bfc() { // Depth-first search
vertexList[0].setVisited(true);
displayVertex(0);
queue.add(0);
int v2;
while (!queue.isEmpty()) {
int v = queue.remove();
while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
vertexList[v2].visited = true;
displayVertex(v2);
queue.add(v2);
}
}
for (int j = 0; j < nVerts; j++) { // Reset the flags
vertexList[j].visited = false;
}
}
private int getAdjUnvisitedVertex(int v) {
for (int j = 0; j < nVerts; j++) {
if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
return j; // Returns the first vertext found
}
}
return -1;
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A'); //0
graph.addVertex('B'); //1
graph.addVertex('C'); //2
graph.addVertex('D'); //3
graph.addVertex('E'); //4
graph.addVertex('F'); //5
graph.addVertex('G'); //6
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(0,3);
graph.addEdge(1,4);
graph.addEdge(3,5);
graph.addEdge(5,6);
System.out.println("Visits: ");
graph.bfc();
}
}
방문수: ABCDEFG
다시 말하지만, 인접 행렬이 있고 루프 내에 중첩된 루프를 사용하므로 위 알고리즘의 시간 복잡도는 O(N²)입니다.
4. Dijkstra 알고리즘
앞서 언급했듯이 그래프는 방향이 지정되거나 방향이 지정되지 않을 수 있습니다. 그리고 가중치도 부여될 수 있다는 것을 기억하실 것입니다. 가중 방향 그래프는 실생활에서 흔히 볼 수 있는 관계를 모델화합니다. 예를 들어 도시가 정점이고 그 사이의 가장자리가 방향 가장자리 방향으로 흐르는 일방통행 교통의 도로인 도시 지도입니다. 당신이 화물 회사이고 멀리 떨어져 있는 두 도시 사이의 최단 경로를 찾아야 한다고 가정해 보겠습니다. 어떻게 하시겠습니까? 두 정점 사이의 최단 경로를 찾는 것은 가중치 그래프를 사용하여 해결되는 가장 일반적인 문제 중 하나입니다. 이 문제를 해결하기 위해 Dijkstra 알고리즘을 사용합니다. 일단 실행하면 주어진 초기 정점에서 다른 모든 정점까지의 최단 경로를 알 수 있습니다. 이 알고리즘의 단계는 무엇입니까? 나는 이 질문에 대답하려고 노력할 것입니다. Dijkstra 알고리즘의 단계:- 1단계: 탐색 비용이 가장 낮은 인접 노드를 찾습니다(가장 낮은 간선 가중치). 당신은 맨 처음에 서서 어디로 갈지 생각하고 있습니다: 노드 A 또는 노드 B. 이러한 각 노드로 이동하는 데 드는 비용은 얼마입니까?
- 2단계: В에서 가장자리를 횡단할 때 알고리즘이 아직 방문하지 않은 노드 В의 모든 이웃까지 이동하는 거리를 계산합니다. 새 거리가 이전 거리보다 작으면 가장자리 B를 통과하는 경로가 이 정점에 대한 새로운 최단 경로가 됩니다.
- 3단계: 정점 B를 방문한 것으로 표시합니다.
- 4단계: 1단계로 이동합니다.
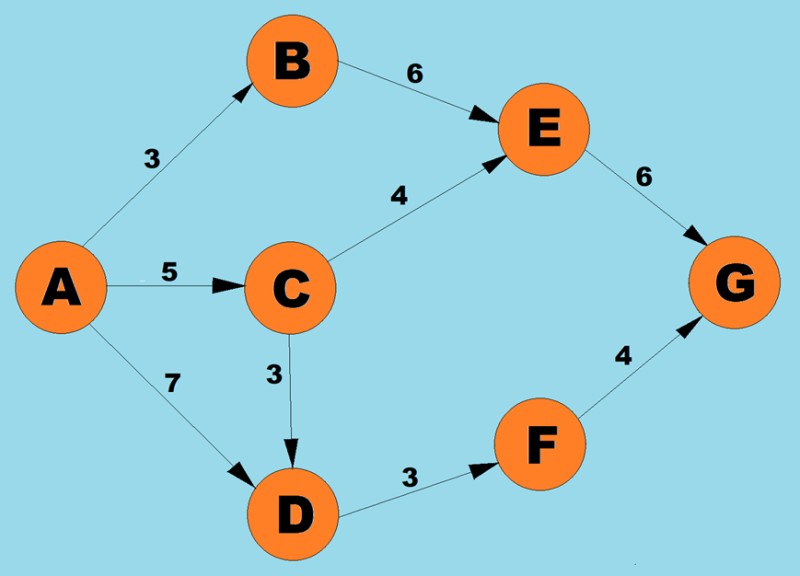위의 알고리즘을 사용하여 A에서 G까지의 최단 경로를 결정합니다.
- 정점 A에는 세 가지 가능한 경로가 있습니다. 가중치가 3인 B, 가중치가 5인 C, 가중치가 7인 D입니다. 알고리즘의 첫 번째 단계에 따라 비용이 가장 낮은 노드(모서리 가중치)를 선택합니다. 이 경우 B.
-
B의 방문하지 않은 유일한 이웃은 정점 Е이므로 이 정점을 통과하면 경로가 무엇인지 확인합니다. 3(AB) + 6(BE) = 9.
따라서 A에서 E까지의 현재 최단 경로는 9라고 기록됩니다.
-
정점 B에 대한 작업이 완료되었으므로 가장자리의 가중치가 최소인 다음 정점을 선택합니다.
정점 A와 B에서 가능한 정점은 D(7), C(5) 또는 E(6)입니다.
С에 대한 가장자리의 가중치가 가장 작으므로 이 정점으로 이동합니다.
-
다음으로, 이전과 마찬가지로 C를 통과할 때 이웃 꼭지점까지의 최단 경로를 찾습니다.
-
AD = 5(AC) + 3(CD) = 8이지만 С를 통해 이전 최단 경로(AC = 7)가 이보다 작으므로 최단 경로(AC = 7)를 변경하지 않고 유지합니다.
-
CE = 5(AC) + 4(CE) = 9. 이 새로운 최단 경로는 이전 경로와 동일하므로 변경하지 않고 그대로 둡니다.
-
-
가장 가까운 접근 가능한 꼭짓점(E와 D)에서 가장자리 가중치가 가장 작은 꼭짓점, 즉 D(3)를 선택합니다.
-
우리는 이웃 F로 가는 최단 경로를 찾습니다.
AF = 7(AD) + 3(DF) = 9
-
가장 가까운 접근 가능한 정점(E 및 F)에서 가장자리 가중치가 가장 작은 정점, 즉 F(3)를 선택합니다.
-
이웃 G까지의 최단 경로를 찾으세요.
AG = 7(AD) + 3(DF) + 4(FG) = 14
그래서 우리는 A에서 G로 가는 길을 찾았습니다.
그러나 이것이 가장 짧은지 확인하려면 정점 E에서도 단계를 수행해야 합니다.
-
정점 G에는 방향이 있는 가장자리가 가리키는 이웃 정점이 없기 때문에 정점 E만 남아 있으므로 이를 선택합니다.
-
이웃 G까지의 최단 경로를 찾습니다.
AG = 3(AB) + 6(BE) + 6(EG) = 15. 이 경로는 이전 최단 경로(AG(14))보다 길기 때문에 이 경로를 변경하지 않고 그대로 둡니다.
G에서 이어지는 정점이 없기 때문에 이 정점에서 알고리즘의 단계를 실행하는 것은 의미가 없습니다. 이는 알고리즘 작업이 완료되었음을 의미합니다.
public class Vertex {
private char label;
private boolean isInTree;
public Vertex(char label) {
this.label = label;
this.isInTree = false;
}
public char getLabel() {
return label;
}
public void setLabel(char label) {
this.label = label;
}
public boolean isInTree() {
return isInTree;
}
public void setInTree(boolean inTree) {
isInTree = inTree;
}
}public class Path { // A class that contains the distance and the previous and traversed vertices
private int distance; // Current distance from the starting vertex
private List parentVertices; // Current parent vertex
public Path(int distance) {
this.distance = distance;
this.parentVertices = new ArrayList<>();
}
public int getDistance() {
return distance;
}
public void setDistance(int distance) {
this.distance = distance;
}
public List getParentVertices() {
return parentVertices;
}
public void setParentVertices(List parentVertices) {
this.parentVertices = parentVertices;
}
}public class Graph {
private final int MAX_VERTS = 10;// Maximum number of vertices
private final int INFINITY = 100000000; // This number represents infinity
private Vertex vertexList[]; // List of vertices
private int relationMatrix[][]; // Matrix of edges between vertices
private int numberOfVertices; // Current number of vertices
private int numberOfVerticesInTree; // Number of visited vertices in the tree
private List shortestPaths; // List of shortest paths
private int currentVertex; // Current vertex
private int startToCurrent; // Distance to currentVertex
public Graph() {
vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
relationMatrix = new int[MAX_VERTS][MAX_VERTS];
numberOfVertices = 0;
numberOfVerticesInTree = 0;
for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
relationMatrix[i][k] = INFINITY; // Assign default values
shortestPaths = new ArrayList<>(); // Assign an empty list
}
}
}
public void addVertex(char lab) {// Assign new vertices
vertexList[numberOfVertices++] = new Vertex(lab);
}
public void addEdge(int start, int end, int weight) {
relationMatrix[start][end] = weight; // Set weighted edges between vertices
}
public void path() { // Choose the shortest path
// Set the initial vertex data
int startTree = 0; // Start from vertex 0
vertexList[startTree].setInTree(true); // Include the first element in the tree
numberOfVerticesInTree = 1;
// Fill out the shortest paths for vertices adjacent to the initial vertex
for (int i = 0; i < numberOfVertices; i++) {
int tempDist = relationMatrix[startTree][i];
Path path = new Path(tempDist);
path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
shortestPaths.add(path);
}
// Until every vertex is in the tree
while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree
if (minDist == INFINITY) {
System.out.println("The graph has an unreachable vertex");
break; // If only unreachable vertices have not been visited, then we exit the loop
} else {
currentVertex = indexMin; // Set currentVert to the index of the current vertex
startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
}
vertexList[currentVertex].setInTree(true); // Add the current vertex to the tree
numberOfVerticesInTree++; // Increase the count of vertices in the tree
updateShortestPaths(); // Update the list of shortest paths
}
displayPaths(); // Display the results on the console
}
public void clear() { // Clear the tree
numberOfVerticesInTree = 0;
for (int i = 0; i < numberOfVertices; i++) {
vertexList[i].setInTree(false);
}
}
private int getMin() {
int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
int indexMin = 0;
for (int i = 1; i < numberOfVertices; i++) { // For each vertex
if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
minDist = shortestPaths.get(i).getDistance(); // then update the minimum
indexMin = i; // Update the index of the vertex with the minimum distance
}
}
return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
}
private void updateShortestPaths() {
int vertexIndex = 1; // The initial vertex is skipped
while (vertexIndex < numberOfVertices) { // Run over the columns
if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
vertexIndex++;
continue;
}
// Calculate the distance for one element sPath
// Get the edge from currentVert to column
int currentToFringe = relationMatrix[currentVertex][vertexIndex];
// Add up all the distances
int startToFringe = startToCurrent + currentToFringe;
// Determine the distance to the current vertexIndex
int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();
// Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
}
vertexIndex++;
}
}
private void displayPaths() { // A method for displaying the shortest paths on the screen
for (int i = 0; i < numberOfVertices; i++) {
System.out.print(vertexList[i].getLabel() + " = ");
if (shortestPaths.get(i).getDistance() == INFINITY) {
System.out.println("0");
} else {
String result = shortestPaths.get(i).getDistance() + " (";
List parents = shortestPaths.get(i).getParentVertices();
for (int j = 0; j < parents.size(); j++) {
result += vertexList[parents.get(j)].getLabel() + " -> ";
}
System.out.println(result + vertexList[i].getLabel() + ")");
}
}
}
}public class Solution {
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addEdge(0, 1, 3);
graph.addEdge(0, 2, 5);
graph.addEdge(0, 3, 7);
graph.addEdge(1, 4, 6);
graph.addEdge(2, 4, 4);
graph.addEdge(2, 3, 3);
graph.addEdge(3, 5, 3);
graph.addEdge(4, 6, 6);
graph.addEdge(5, 6, 4);
System.out.println("The following nodes form the shortest paths from node A:");
graph.path();
graph.clear();
}
}
다음 노드는 노드 A에서 최단 경로를 형성합니다. A = 0 B = 3 (A -> B) C = 5 (A -> C) D = 7 (A -> D) E = 9 (A -> B - > E) F = 10 (A -> D -> F) G = 14 (A -> D -> F -> G)
이 알고리즘의 시간 복잡도는 다름 아닌 O(N²)입니다. 중첩된 루프가 있기 때문입니다. 오늘 제가 가진 것은 그게 전부입니다. 주목 해 주셔서 감사합니다!
GO TO FULL VERSION