Le domande e risposte dei colloqui di lavoro: algoritmi in Java, parte 2

Questa è la seconda parte di una breve panoramica sugli algoritmi. Ecco il link al primo articolo . In precedenza abbiamo esaminato vari algoritmi per l'ordinamento degli array, nonché il cosiddetto algoritmo greedy. Oggi parleremo dei grafici e degli algoritmi ad essi associati. Un grafico è una delle strutture più flessibili e versatili nella programmazione. Il grafo G è solitamente definito da una coppia di insiemi, ovvero G = (V, R), dove:

• V è un insieme di vertici;
• R è un insieme di linee che collegano coppie di vertici.

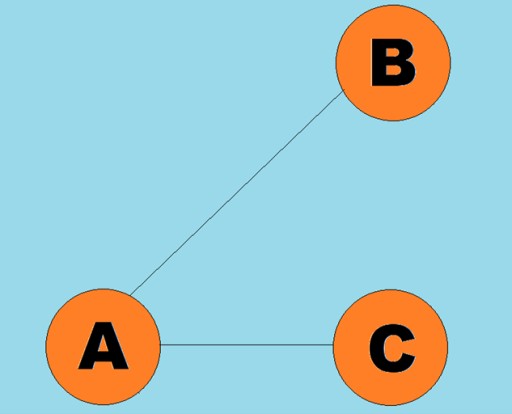Le linee di collegamento non orientate sono chiamate spigoli: Le linee dirette sono chiamate archi: 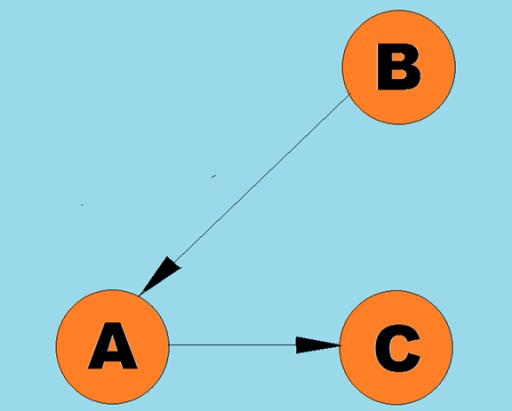Tipicamente, un grafico è rappresentato da un diagramma in cui alcuni vertici sono collegati da spigoli (archi). I grafici i cui bordi indicano una direzione di attraversamento sono chiamati grafici diretti. Se un grafo è connesso da archi che non indicano la direzione di attraversamento, allora diciamo che è un grafo non orientato. Ciò significa che il movimento è possibile in entrambe le direzioni: sia dal vertice A al vertice B, sia dal vertice B al vertice A. Un grafo connesso è un grafo in cui almeno un percorso conduce da ciascun vertice a qualsiasi altro vertice (come nel esempio sopra). In caso contrario il grafico si dice sconnesso: è 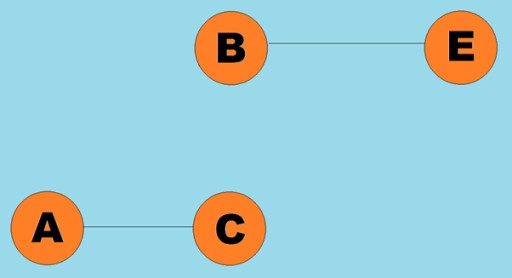possibile assegnare pesi anche agli archi (archi). I pesi sono numeri che rappresentano, ad esempio, la distanza fisica tra due vertici (o il tempo di percorrenza relativo tra due vertici). Questi grafici sono chiamati grafici ponderati: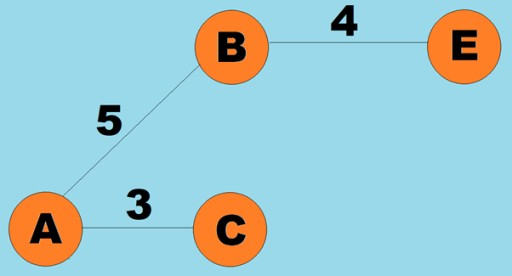

3. Algoritmi di pathfinding (profondità prima, ampiezza prima)

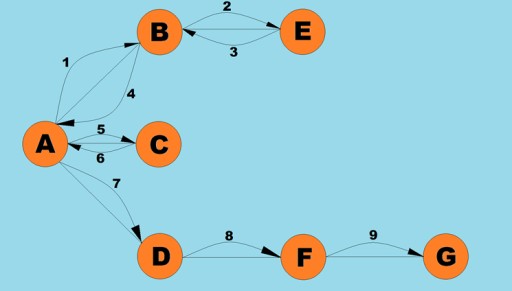
Una delle operazioni fondamentali eseguite con i grafici è determinare tutti i vertici raggiungibili da un dato vertice. Immagina di provare a determinare come viaggiare in autobus da una città all'altra, compresi i possibili trasferimenti. Alcune città possono essere raggiunte direttamente, mentre altre possono essere raggiunte solo passando per altre città. Esistono molte altre situazioni in cui potresti dover trovare tutti i vertici che puoi raggiungere da un dato vertice. Esistono due modi principali per attraversare i grafici: prima in profondità e prima in ampiezza. Esploreremo entrambi questi aspetti. Entrambi i metodi attraversano tutti i vertici connessi. Per esplorare ulteriormente gli algoritmi deep-first e width-first, utilizzeremo il seguente grafico:

Ricerca in profondità

Questo è uno dei metodi di attraversamento del grafico più comuni. La strategia deep-first consiste nell'andare il più in profondità possibile in un grafico. Quindi, dopo aver raggiunto un vicolo cieco, torniamo al vertice più vicino che ha vertici adiacenti precedentemente non visitati. Questo algoritmo memorizza le informazioni nello stack su dove tornare quando viene raggiunto un vicolo cieco. Regole per la ricerca approfondita:

1. Visita un vertice adiacente precedentemente non visitato, contrassegnalo come visitato e mettilo nello stack.
2. Spostarsi su questo vertice.
3. Ripetere il passaggio 1.
4. Se il passo 1 è impossibile, torna al vertice precedente e prova a eseguire il passo 1. Se ciò non è possibile, torna al vertice precedente e così via, finché non troviamo un vertice dal quale possiamo continuare la traversata.
5. Continua finché tutti i vertici non sono in pila.

Diamo un'occhiata a come potrebbe apparire il codice Java per questo algoritmo:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

Un vertice assomiglia a questo:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

Eseguiamo questo algoritmo con vertici specifici e vediamo se funziona correttamente:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

Uscita console: Poiché abbiamo una matrice di adiacenza e stiamo utilizzando un ciclo all'interno di un ciclo, la complessità temporale sarà O(N²).

Ricerca in ampiezza

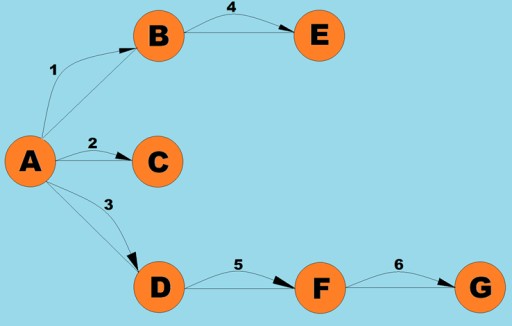
Come la ricerca approfondita, questo algoritmo è uno dei metodi di attraversamento del grafico più semplici e basilari. L'essenza è che abbiamo qualche vertice attuale. Mettiamo in coda tutti i suoi vertici adiacenti non visitati e selezioniamo l'elemento successivo (che è il vertice memorizzato in testa alla coda), che diventa il vertice corrente… Suddividendo questo algoritmo in fasi, possiamo identificare i seguenti passaggi:

1. Visita il successivo vertice precedentemente non visitato adiacente al vertice corrente, contrassegnalo in anticipo come visitato e aggiungilo alla coda.
2. Se il passaggio n. 1 non può essere eseguito, rimuovere il vertice dalla coda e renderlo il vertice corrente.
3. Se i passaggi n. 1 e n. 2 non possono essere eseguiti, l'attraversamento è terminato: ogni vertice è stato attraversato (se abbiamo un grafico connesso).

La classe del grafico qui è quasi identica a quella che abbiamo usato per l'algoritmo di ricerca deep-first, ad eccezione del metodo di ricerca stesso e del fatto che una coda sostituisce lo stack interno:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

La classe Vertex è identica a quella che abbiamo utilizzato con l'algoritmo di ricerca deep-first. Mettiamo in azione questo algoritmo:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

Uscita console: Ancora: abbiamo una matrice di adiacenza e utilizziamo un ciclo annidato all'interno di un ciclo, quindi la complessità temporale dell'algoritmo sopra è O(N²).

4. Algoritmo di Dijkstra

Come accennato in precedenza, i grafici possono essere diretti o non orientati. E ricorderai che possono anche essere ponderati. I grafici ponderati e diretti modellano le relazioni che spesso si trovano nella vita reale: ad esempio, una mappa di città in cui le città sono i vertici e i bordi tra loro sono strade con traffico a senso unico, che scorrono nella direzione del bordo diretto. Diciamo che sei un'azienda di trasporti e devi trovare il percorso più breve tra due città distanti. Come lo faresti? Trovare il percorso più breve tra due vertici è uno dei problemi più comuni risolti utilizzando i grafici pesati. Per risolvere questo problema utilizziamo l'algoritmo di Dijkstra. Una volta eseguito, conoscerai i percorsi più brevi da un dato vertice iniziale a tutti gli altri. Quali sono i passaggi di questo algoritmo? Proverò a rispondere a questa domanda. Passi dell'algoritmo di Dijkstra:

• Passaggio 1: trovare il nodo adiacente che ha il costo più basso verso cui navigare (peso del bordo più basso). Ti trovi proprio all'inizio e stai pensando a dove andare: al nodo A o al nodo B. Qual è il costo per spostarsi verso ciascuno di questi nodi?
• Passaggio 2: calcolare la distanza da percorrere verso tutti i vicini del nodo В che non sono stati ancora visitati dall'algoritmo quando si attraversa il bordo da В. Se la nuova distanza è inferiore a quella vecchia, allora il percorso attraverso il bordo B diventa il nuovo percorso più breve per questo vertice.
• Passaggio 3: contrassegnare il vertice B come visitato.
• Passaggio 4: vai al passaggio 1.

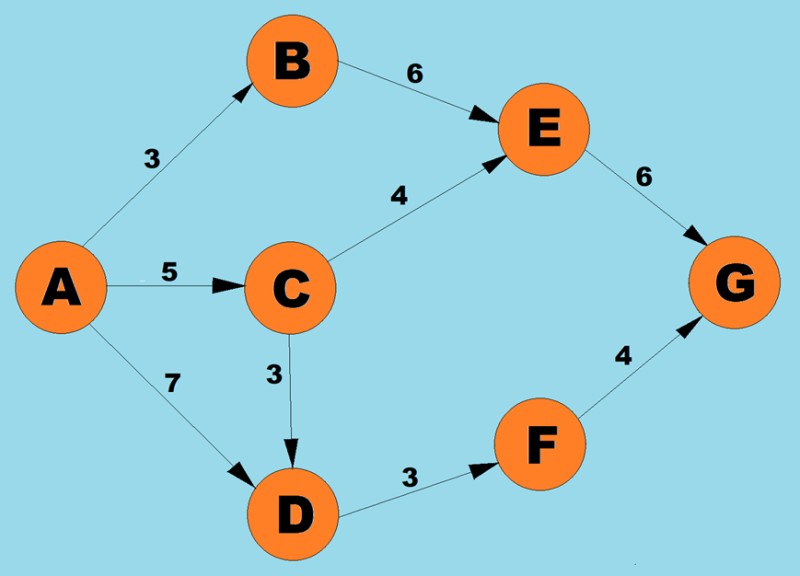Ripeteremo questi passaggi in loop finché tutti i vertici non saranno stati visitati. Consideriamo il seguente grafico diretto ponderato: Utilizzando l'algoritmo sopra, determineremo il percorso più breve da A a G:

1. Ci sono tre possibili percorsi per il vertice A: verso B con peso 3, verso С con peso 5 e verso D con peso 7. Secondo il primo passo dell'algoritmo, selezioniamo il nodo con il costo più basso (peso del bordo). In questo caso, B.

2. Dato che l'unico vicino non visitato di B è il vertice Å, controlliamo quale sarebbe il percorso se passassimo per questo vertice. 3(AB) + 6(BE) = 9.

   Pertanto, registriamo che l'attuale percorso più breve da A a E è 9.

3. Poiché il nostro lavoro con il vertice B è completo, procediamo alla selezione del vertice successivo il cui bordo ha il peso minimo.

   Dai vertici A e B, le possibilità sono i vertici D (7), C (5) o E (6).

   Il bordo verso С ha il peso più piccolo, quindi andiamo su questo vertice.

4. Successivamente, come prima, troviamo il percorso più breve verso i vertici vicini quando si passa attraverso C:

   • AD = 5 (AC) + 3 (CD) = 8, ma poiché il percorso più breve precedente (AC = 7) è inferiore a questo attraverso С, manteniamo invariato il percorso più breve (AC = 7).

   • CE = 5(AC) + 4(CE) = 9. Questo nuovo cammino minimo è uguale al precedente, quindi lo lasciamo invariato.

5. Dai vertici accessibili più vicini (E e D), seleziona il vertice con il peso del bordo più piccolo, cioè D (3).

6. Troviamo il percorso più breve verso il suo vicino F.

   AF = 7(AD) + 3(DF) = 9

7. Dai vertici accessibili più vicini (E e F), seleziona il vertice con il peso del bordo più piccolo, cioè F (3).

8. Trova il percorso più breve verso il suo vicino G.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   Quindi, abbiamo trovato un percorso da A a G.

   Ma per essere sicuri che sia il più corto dobbiamo eseguire i nostri passi anche sul vertice E.

9. Poiché il vertice G non ha vertici vicini puntati da bordi diretti, ci rimane solo il vertice E, quindi lo scegliamo.

10. Trova il percorso più breve per il vicino G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Questo percorso è più lungo del percorso più breve precedente (AG (14)), quindi lasciamo questo percorso invariato.

    Poiché non ci sono vertici che partono da G, non ha senso eseguire i passaggi dell'algoritmo su questo vertice. Ciò significa che il lavoro dell’algoritmo è completo.

Come ho detto prima, oltre a trovare il cammino più breve per AG, abbiamo anche ottenuto i cammini più brevi dal vertice A a ogni altro vertice (AB, AC, AD, AE, AF). Bene, ora è il momento di dare un'occhiata a come è possibile farlo in Java. Cominciamo con la classe dei vertici:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

La classe dei vertici è praticamente identica alla classe dei vertici utilizzata per la ricerca in ampiezza. Per visualizzare i percorsi più brevi, abbiamo bisogno di una nuova classe che conterrà i dati di cui abbiamo bisogno:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

In questa classe possiamo vedere la distanza totale del percorso e i vertici che verranno attraversati passando lungo il percorso più breve. E ora diamo un'occhiata alla classe in cui effettivamente percorriamo il percorso più breve nel grafico. Quindi qui abbiamo la classe Graph:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

Quindi questa è tutta la magia =) Ora diamo un'occhiata a questo algoritmo in azione:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

E l'output della console è questo: La complessità temporale di questo algoritmo non è altro che O(N²), poiché abbiamo cicli annidati. Questo è tutto quello che ho oggi. Grazie per l'attenzione!