Hỏi đáp từ phỏng vấn xin việc: thuật toán trong Java, phần 2

Đây là phần thứ hai của tổng quan ngắn gọn về các thuật toán. Đây là một liên kết đến bài viết đầu tiên . Trước đó chúng ta đã xem xét các thuật toán khác nhau để sắp xếp mảng cũng như thuật toán được gọi là thuật toán tham lam. Hôm nay chúng ta sẽ nói về đồ thị và các thuật toán liên quan đến chúng. Biểu đồ là một trong những cấu trúc linh hoạt và linh hoạt nhất trong lập trình. Đồ thị G thường được xác định bởi một cặp tập hợp, tức là G = (V, R), trong đó:

• V là tập các đỉnh;
• R là tập hợp các đường nối các cặp đỉnh.

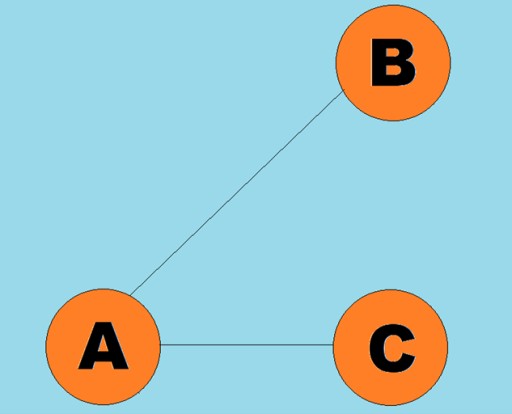Các đường nối vô hướng được gọi là các cạnh: Các đường có hướng được gọi là các cung: 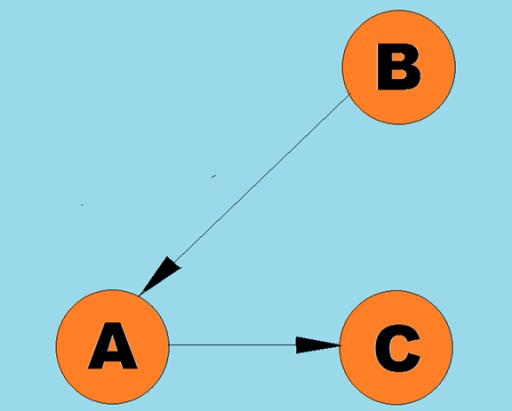Thông thường, một đồ thị được biểu diễn bằng một sơ đồ trong đó một số đỉnh được nối với nhau bằng các cạnh (cung). Đồ thị có các cạnh biểu thị hướng truyền tải được gọi là đồ thị có hướng. Nếu một đồ thị được nối bởi các cạnh không chỉ hướng truyền thì ta nói đó là đồ thị vô hướng. Điều này có nghĩa là có thể chuyển động theo cả hai hướng: cả từ đỉnh A đến đỉnh B và từ đỉnh B đến đỉnh A. Đồ thị liên thông là một đồ thị trong đó có ít nhất một đường dẫn từ mỗi đỉnh đến bất kỳ đỉnh nào khác (như trong ví dụ ở trên). Nếu không đúng như vậy thì đồ thị được cho là không liên kết: 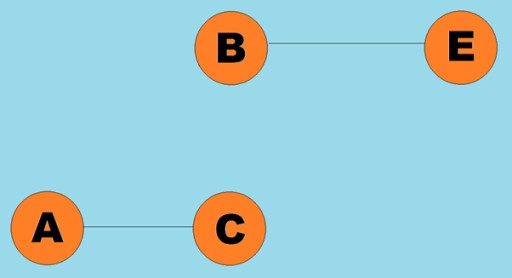Trọng số cũng có thể được gán cho các cạnh (cung). Trọng số là những con số biểu thị, ví dụ, khoảng cách vật lý giữa hai đỉnh (hoặc thời gian di chuyển tương đối giữa hai đỉnh). Những đồ thị này được gọi là đồ thị có trọng số: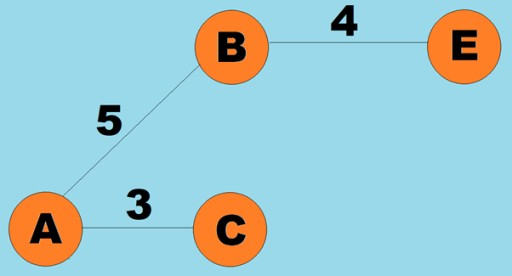

3. Thuật toán tìm đường (theo chiều sâu, theo chiều rộng)

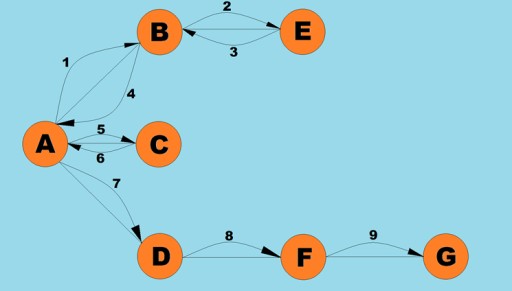
Một trong những thao tác cơ bản được thực hiện với đồ thị là xác định tất cả các đỉnh có thể tiếp cận được từ một đỉnh đã cho. Hãy tưởng tượng rằng bạn đang cố gắng xác định cách bạn có thể đi xe buýt từ thành phố này sang thành phố khác, bao gồm cả khả năng chuyển tuyến. Một số thành phố có thể đến trực tiếp, trong khi một số thành phố chỉ có thể đến được bằng cách đi qua các thành phố khác. Có nhiều tình huống khác mà bạn có thể cần tìm tất cả các đỉnh mà bạn có thể chạm tới từ một đỉnh cho trước. Có hai cách chính để duyệt đồ thị: theo chiều sâu và theo chiều rộng. Chúng ta sẽ khám phá cả hai điều này. Cả hai phương pháp đều đi qua tất cả các đỉnh được kết nối. Để khám phá thêm các thuật toán theo chiều sâu và chiều rộng, chúng tôi sẽ sử dụng biểu đồ sau:

Tìm kiếm theo chiều sâu

Đây là một trong những phương pháp duyệt đồ thị phổ biến nhất. Chiến lược theo chiều sâu là đi sâu nhất có thể vào biểu đồ. Sau khi đi đến ngõ cụt, chúng ta quay trở lại đỉnh gần nhất mà trước đó chưa được thăm các đỉnh liền kề. Thuật toán này lưu trữ thông tin trên ngăn xếp về nơi cần quay lại khi đi đến ngõ cụt. Quy tắc tìm kiếm theo chiều sâu:

1. Thăm một đỉnh liền kề chưa được thăm trước đó, đánh dấu nó là đã thăm và đẩy nó vào ngăn xếp.
2. Di chuyển đến đỉnh này.
3. Lặp lại bước 1.
4. Nếu bước 1 không thể thực hiện được, hãy quay lại đỉnh trước đó và thử thực hiện bước 1. Nếu không thể, hãy quay lại đỉnh trước đỉnh đó, v.v., cho đến khi chúng ta tìm thấy một đỉnh mà từ đó chúng ta có thể tiếp tục quá trình truyền tải.
5. Tiếp tục cho đến khi tất cả các đỉnh đều nằm trong ngăn xếp.

Chúng ta hãy xem mã Java cho thuật toán này trông như thế nào:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexArray[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Stack stack;

  public Graph() { // Initialize internal fields
     vertexArray = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {
           adjMat[j][k] = 0;
        }
     }
     stack = new Stack<>();
  }

  public void addVertex(char lab) {
     vertexArray[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexArray[v].getLabel());
  }

  public void dfs() { // Depth-first search
     vertexArray[0].setVisited(true); // Take the first vertex
     displayVertex(0);
     stack.push(0);

     while (!stack.empty()) {
        int v = getAdjUnvisitedVertex(stack.peek()); // Return the index of the adjacent vertex: if any, 1; if not, -1
        if (v == -1) { // If there is no unvisited adjacent vertex
           stack.pop(); // The element is removed from the stack
        }
        else {
           vertexArray[v].setVisited(true);
           displayVertex(v);
           stack.push(v); // The element goes on top of the stack
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexArray[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexArray[j].visited == false) {
           return j; // Returns the first vertex found
        }
     }
     return -1;
  }
}

Một đỉnh trông như thế này:

public class Vertex {
  private char label;  // for example, 'A'
  public boolean visited;

  public Vertex(final char label) {
     this.label = label;
     visited = false;
  }

  public char getLabel() {
     return this.label;
  }

  public boolean isVisited() {
     return this.visited;
  }

  public void setVisited(final boolean visited) {
     this.visited = visited;
  }
}

Hãy chạy thuật toán này với các đỉnh cụ thể và xem nó có hoạt động chính xác không:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.dfs();
  }
}

Đầu ra của bảng điều khiển: Vì chúng ta có ma trận kề và đang sử dụng một vòng lặp trong một vòng lặp nên độ phức tạp về thời gian sẽ là O(N2).

Tìm kiếm theo chiều rộng

Giống như tìm kiếm theo chiều sâu, thuật toán này là một trong những phương pháp duyệt đồ thị đơn giản và cơ bản nhất. Ý chính là chúng ta có một số đỉnh hiện tại. Chúng ta đặt tất cả các đỉnh liền kề chưa được thăm của nó vào một hàng đợi và chọn phần tử tiếp theo (là đỉnh được lưu ở đầu hàng đợi), trở thành đỉnh hiện tại… Chia thuật toán này thành các giai đoạn, chúng ta có thể xác định các bước sau:

1. Truy cập đỉnh tiếp theo chưa được thăm trước đó liền kề với đỉnh hiện tại, đánh dấu đỉnh đó là đã ghé thăm trước và thêm nó vào hàng đợi.
2. Nếu bước #1 không thể thực hiện được thì hãy xóa đỉnh đó khỏi hàng đợi và đặt nó làm đỉnh hiện tại.
3. Nếu bước #1 và #2 không thể thực hiện được thì chúng ta đã đi ngang xong - mọi đỉnh đều đã được đi qua (nếu chúng ta có một đồ thị liên thông).

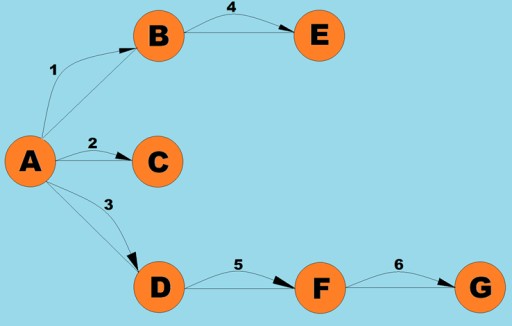Lớp biểu đồ ở đây gần giống với lớp chúng tôi đã sử dụng cho thuật toán tìm kiếm theo chiều sâu, ngoại trừ chính phương thức tìm kiếm và thực tế là hàng đợi thay thế ngăn xếp bên trong:

public class Graph {
  private final int MAX_VERTS = 10;
  private Vertex vertexList[]; // Array of vertices
  private int adjMat[][]; // Adjacency matrix
  private int nVerts; // Current number of vertices
  private Queue queue;

  public Graph() {
     vertexList = new Vertex[MAX_VERTS];
     adjMat = new int[MAX_VERTS][MAX_VERTS];
     nVerts = 0;
     for (int j = 0; j < MAX_VERTS; j++) {
        for (int k = 0; k < MAX_VERTS; k++) {  // Fill the adjacency matrix with zeros
           adjMat[j][k] = 0;
        }
     }
     queue = new PriorityQueue<>();
  }

  public void addVertex(char lab) {
     vertexList[nVerts++] = new Vertex(lab);
  }

  public void addEdge(int start, int end) {
     adjMat[start][end] = 1;
     adjMat[end][start] = 1;
  }

  public void displayVertex(int v) {
     System.out.println(vertexList[v].getLabel());
  }

  public void bfc() { // Depth-first search
     vertexList[0].setVisited(true);
     displayVertex(0);
     queue.add(0);
     int v2;

     while (!queue.isEmpty()) {
        int v = queue.remove();

        while((v2 = getAdjUnvisitedVertex(v))!=-1) {// The loop runs until every adjacent vertex is found and added to the queue
           vertexList[v2].visited = true;
           displayVertex(v2);
           queue.add(v2);
        }
     }

     for (int j = 0; j < nVerts; j++) {  // Reset the flags
        vertexList[j].visited = false;
     }

  }

  private int getAdjUnvisitedVertex(int v) {
     for (int j = 0; j < nVerts; j++) {
        if (adjMat[v][j] == 1 && vertexList[j].visited == false) {
           return j; // Returns the first vertext found
        }
     }
     return -1;
  }
}

Lớp Vertex giống hệt với lớp chúng tôi đã sử dụng với thuật toán tìm kiếm theo chiều sâu. Hãy áp dụng thuật toán này vào hoạt động:

public class Solution {
  public static void main(String[] args) {
     Graph graph = new Graph();
     graph.addVertex('A'); //0
     graph.addVertex('B'); //1
     graph.addVertex('C'); //2
     graph.addVertex('D'); //3
     graph.addVertex('E'); //4
     graph.addVertex('F'); //5
     graph.addVertex('G'); //6

     graph.addEdge(0,1);
     graph.addEdge(0,2);
     graph.addEdge(0,3);
     graph.addEdge(1,4);
     graph.addEdge(3,5);
     graph.addEdge(5,6);

     System.out.println("Visits: ");
     graph.bfc();
  }
}

Đầu ra của bảng điều khiển: Một lần nữa: chúng ta có ma trận kề và sử dụng một vòng lặp được lồng trong một vòng lặp, do đó độ phức tạp về thời gian của thuật toán trên là O(N²).

4. Thuật toán Dijkstra

Như đã đề cập trước đó, đồ thị có thể có hướng hoặc vô hướng. Và bạn sẽ nhớ lại rằng chúng cũng có thể được cân. Các mối quan hệ trong mô hình đồ thị có hướng, có trọng số thường thấy trong đời thực: ví dụ: bản đồ các thành phố trong đó các thành phố là các đỉnh và các cạnh giữa chúng là những con đường có lưu lượng một chiều, chạy theo hướng của cạnh có hướng. Giả sử bạn là một công ty vận tải hàng hóa và bạn cần tìm con đường ngắn nhất giữa hai thành phố xa xôi. Bạn sẽ làm điều này như thế nào? Tìm đường đi ngắn nhất giữa hai đỉnh là một trong những vấn đề phổ biến nhất được giải quyết bằng cách sử dụng đồ thị có trọng số. Để giải quyết vấn đề này, chúng tôi sử dụng thuật toán Dijkstra. Khi chạy nó, bạn sẽ biết đường đi ngắn nhất từ ​​một đỉnh ban đầu nhất định đến mọi đỉnh khác. Các bước của thuật toán này là gì? Tôi sẽ cố gắng trả lời câu hỏi này. Các bước của thuật toán Dijkstra:

• Bước 1: Tìm nút liền kề có chi phí điều hướng đến thấp nhất (trọng số cạnh thấp nhất). Bạn đang đứng ngay từ đầu và suy nghĩ xem mình sẽ đi đâu: đến nút A hay nút B. Chi phí di chuyển đến từng nút này là bao nhiêu?
• Bước 2: tính khoảng cách di chuyển đến tất cả các nút lân cận của nút B mà thuật toán chưa truy cập khi đi qua cạnh từ nút B. Nếu khoảng cách mới nhỏ hơn khoảng cách cũ thì đường đi qua cạnh B sẽ trở thành đường đi ngắn nhất mới cho đỉnh này.
• Bước 3: đánh dấu đỉnh B là đã thăm.
• Bước 4: Chuyển sang bước 1.

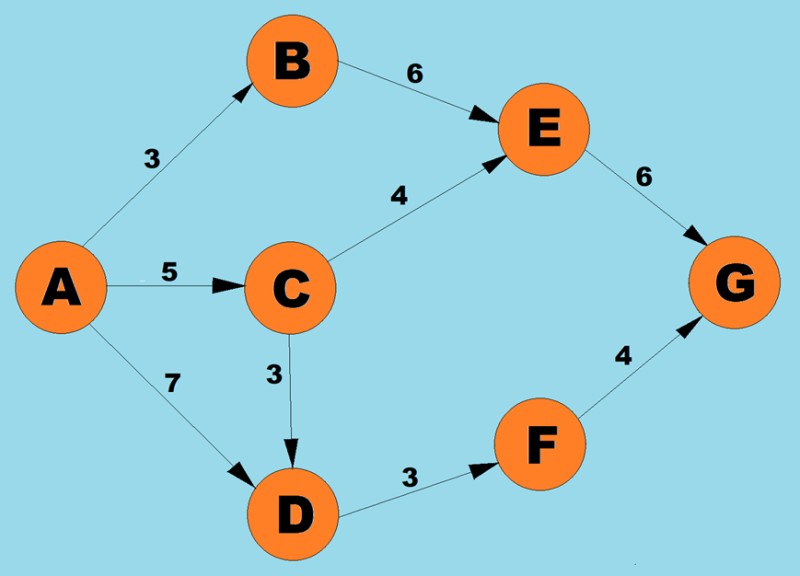Chúng ta sẽ lặp lại các bước này theo vòng lặp cho đến khi đã thăm hết tất cả các đỉnh. Hãy xem xét đồ thị có hướng có trọng số sau: Sử dụng thuật toán trên, chúng ta sẽ xác định đường đi ngắn nhất từ ​​A đến G:

1. Có ba đường dẫn có thể có cho đỉnh A: đến B có trọng số 3, đến С có trọng số 5 và đến D có trọng số 7. Theo bước đầu tiên của thuật toán, chúng ta chọn nút có chi phí thấp nhất (trọng số cạnh). Trong trường hợp này, B

2. Vì hàng xóm duy nhất chưa được thăm của B là đỉnh Е, nên chúng ta kiểm tra đường đi sẽ như thế nào nếu chúng ta đi qua đỉnh này. 3(AB) + 6(BE) = 9.

   Do đó, chúng ta ghi lại rằng đường đi ngắn nhất hiện tại từ A đến E là 9.

3. Vì công việc của chúng ta với đỉnh B đã hoàn tất nên chúng ta tiến hành chọn đỉnh tiếp theo có cạnh có trọng số nhỏ nhất.

   Từ các đỉnh A và B, các khả năng là các đỉnh D (7), C (5) hoặc E (6).

   Cạnh С có trọng số nhỏ nhất nên chúng ta đi tới đỉnh này.

4. Tiếp theo, như trước, ta tìm đường đi ngắn nhất tới các đỉnh lân cận khi đi qua C:

   • AD = 5 (AC) + 3 (CD) = 8, nhưng vì đường đi ngắn nhất trước đó (AC = 7) nhỏ hơn đường đi ngắn nhất trước đó qua С nên chúng ta giữ nguyên đường đi ngắn nhất (AC = 7).

   • CE = 5(AC) + 4(CE) = 9. Đường đi ngắn nhất mới này bằng đường đi ngắn nhất trước đó nên chúng ta cũng giữ nguyên.

5. Từ các đỉnh có thể truy cập gần nhất (E và D), chọn đỉnh có trọng số cạnh nhỏ nhất, tức là D (3).

6. Chúng ta tìm đường đi ngắn nhất tới hàng xóm của nó là F.

   AF = 7(AD) + 3(DF) = 9

7. Từ các đỉnh có thể truy cập gần nhất (E và F), chọn đỉnh có trọng số cạnh nhỏ nhất, tức là F (3).

8. Tìm đường đi ngắn nhất tới hàng xóm G của nó.

   AG = 7(AD) + 3(DF) + 4(FG) = 14

   Vì vậy, chúng tôi đã tìm thấy một con đường từ A đến G.

   Nhưng để đảm bảo nó ngắn nhất, chúng ta cũng phải thực hiện các bước trên đỉnh E.

9. Vì đỉnh G không có đỉnh lân cận nào được chỉ ra bởi các cạnh có hướng nên chúng ta chỉ còn lại đỉnh E nên chọn nó.

10. Tìm đường đi ngắn nhất tới hàng xóm G.

    AG = 3 (AB) + 6 (BE) + 6 (EG) = 15. Đường đi này dài hơn đường đi ngắn nhất trước đó (AG(14)) nên ta giữ nguyên đường đi này.

    Vì không có đỉnh nào bắt đầu từ G nên việc chạy các bước của thuật toán trên đỉnh này là vô nghĩa. Điều đó có nghĩa là công việc của thuật toán đã hoàn tất.

Như tôi đã nói trước đó, ngoài việc tìm đường đi ngắn nhất cho AG, chúng ta còn tìm được đường đi ngắn nhất từ ​​đỉnh A đến mọi đỉnh khác (AB, AC, AD, AE, AF). Bây giờ là lúc xem xét cách thực hiện điều này trong Java. Hãy bắt đầu với lớp đỉnh:

public class Vertex {
   private char label;
   private boolean isInTree;

   public Vertex(char label) {
       this.label = label;
       this.isInTree = false;
   }

   public char getLabel() {
       return label;
   }

   public void setLabel(char label) {
       this.label = label;
   }

   public boolean isInTree() {
       return isInTree;
   }

   public void setInTree(boolean inTree) {
       isInTree = inTree;
   }
}

Lớp đỉnh gần như giống với lớp đỉnh được sử dụng cho tìm kiếm theo chiều rộng. Để hiển thị các đường đi ngắn nhất, chúng ta cần một lớp mới chứa dữ liệu chúng ta cần:

public class Path { // A class that contains the distance and the previous and traversed vertices
   private int distance; // Current distance from the starting vertex
   private List parentVertices; // Current parent vertex

   public Path(int distance) {
       this.distance = distance;
       this.parentVertices = new ArrayList<>();
   }

   public int getDistance() {
       return distance;
   }

   public void setDistance(int distance) {
       this.distance = distance;
   }

   public List getParentVertices() {
       return parentVertices;
   }

   public void setParentVertices(List parentVertices) {
       this.parentVertices = parentVertices;
   }
}

Trong lớp này, chúng ta có thể thấy tổng khoảng cách của đường đi và các đỉnh sẽ đi qua khi đi dọc theo đường đi ngắn nhất. Và bây giờ hãy xem lớp mà chúng ta thực sự đi qua con đường ngắn nhất qua biểu đồ. Vì vậy, ở đây chúng ta có lớp Graph:

public class Graph {
   private final int MAX_VERTS = 10;// Maximum number of vertices
   private final int INFINITY = 100000000; // This number represents infinity
   private Vertex vertexList[]; // List of vertices
   private int relationMatrix[][]; // Matrix of edges between vertices
   private int numberOfVertices; // Current number of vertices
   private int numberOfVerticesInTree; // Number of visited vertices in the tree
   private List shortestPaths; // List of shortest paths
   private int currentVertex; // Current vertex
   private int startToCurrent; // Distance to currentVertex

   public Graph() {
       vertexList = new Vertex[MAX_VERTS]; // Adjacency matrix
       relationMatrix = new int[MAX_VERTS][MAX_VERTS];
       numberOfVertices = 0;
       numberOfVerticesInTree = 0;
       for (int i = 0; i < MAX_VERTS; i++) { // Fill the adjacency matrix
           for (int k = 0; k < MAX_VERTS; k++) { // with "infinity"
               relationMatrix[i][k] = INFINITY; // Assign default values
               shortestPaths = new ArrayList<>(); // Assign an empty list
           }
       }
   }

   public void addVertex(char lab) {// Assign new vertices
       vertexList[numberOfVertices++] = new Vertex(lab);
   }

   public void addEdge(int start, int end, int weight) {
       relationMatrix[start][end] = weight; // Set weighted edges between vertices
   }

   public void path() { // Choose the shortest path
       // Set the initial vertex data
       int startTree = 0; // Start from vertex 0
       vertexList[startTree].setInTree(true); // Include the first element in the tree
       numberOfVerticesInTree = 1;

       // Fill out the shortest paths for vertices adjacent to the initial vertex
       for (int i = 0; i < numberOfVertices; i++) {
           int tempDist = relationMatrix[startTree][i];
           Path path = new Path(tempDist);
           path.getParentVertices().add(0);// The starting vertex will always be a parent vertex
           shortestPaths.add(path);
       }
       // Until every vertex is in the tree
       while (numberOfVerticesInTree < numberOfVertices) { // Do this until the number of of vertices in the tree equals the total number of vertices
           int indexMin = getMin();// Get the index of the of the vertex with the smallest distance from the vertices not yet in the tree
           int minDist = shortestPaths.get(indexMin).getDistance(); // Minimum distance to the vertices not yet in the tree

           if (minDist == INFINITY) {
               System.out.println("The graph has an unreachable vertex");
               break; // If only unreachable vertices have not been visited, then we exit the loop
           } else {
               currentVertex = indexMin; // Set currentVert to the index of the current vertex
               startToCurrent = shortestPaths.get(indexMin).getDistance(); // Set the distance to the current vertex
           }

           vertexList[currentVertex].setInTree(true);  // Add the current vertex to the tree
           numberOfVerticesInTree++; // Increase the count of vertices in the tree
           updateShortestPaths(); // Update the list of shortest paths
       }

       displayPaths(); // Display the results on the console
   }

   public void clear() { // Clear the tree
       numberOfVerticesInTree = 0;
       for (int i = 0; i < numberOfVertices; i++) {
           vertexList[i].setInTree(false);
       }
   }

   private int getMin() {
       int minDist = INFINITY; // The distance of the initial shortest path is taken to be infinite
       int indexMin = 0;
       for (int i = 1; i < numberOfVertices; i++) { // For each vertex
           if (!vertexList[i].isInTree() && shortestPaths.get(i).getDistance() < minDist) { // If the vertex is not yet in the tree and the distance to the vertex is less than the current minimum
               minDist = shortestPaths.get(i).getDistance(); // then update the minimum
               indexMin = i; // Update the index of the vertex with the minimum distance
           }
       }
       return indexMin; // Returns the index of the vertex with the smallest distance among those not yet in the tree
   }

   private void updateShortestPaths() {
       int vertexIndex = 1; // The initial vertex is skipped
       while (vertexIndex < numberOfVertices) { // Run over the columns

           if (vertexList[vertexIndex].isInTree()) { // If the column vertex is already in the tree, then we skip it
               vertexIndex++;
               continue;
           }
           // Calculate the distance for one element sPath
           // Get the edge from currentVert to column
           int currentToFringe = relationMatrix[currentVertex][vertexIndex];
           // Add up all the distances
           int startToFringe = startToCurrent + currentToFringe;
           // Determine the distance to the current vertexIndex
           int shortPathDistance = shortestPaths.get(vertexIndex).getDistance();

           // Compare the distance through currentVertex with the current distance in the vertex with index vertexIndex
           if (startToFringe < shortPathDistance) { // If it is smaller, then the vertex at vertexIndex is assigned the new shortest path
               List newParents = new ArrayList<>(shortestPaths.get(currentVertex).getParentVertices()); // Create a copy of the list of vertices of vertex currentVert's parents
               newParents.add(currentVertex); // And add currentVertex to it as the previous vertex
               shortestPaths.get(vertexIndex).setParentVertices(newParents); // Save the new path
               shortestPaths.get(vertexIndex).setDistance(startToFringe); // Save the new distance
           }
           vertexIndex++;
       }
   }

   private void displayPaths() { // A method for displaying the shortest paths on the screen
       for (int i = 0; i < numberOfVertices; i++) {
           System.out.print(vertexList[i].getLabel() + " = ");
           if (shortestPaths.get(i).getDistance() == INFINITY) {
               System.out.println("0");
           } else {
               String result = shortestPaths.get(i).getDistance() + " (";
               List parents = shortestPaths.get(i).getParentVertices();
               for (int j = 0; j < parents.size(); j++) {
                   result += vertexList[parents.get(j)].getLabel() + " -> ";
               }
               System.out.println(result + vertexList[i].getLabel() + ")");
           }
       }
   }
}

Vậy đó là tất cả điều kỳ diệu =) Bây giờ, chúng ta hãy xem thuật toán này hoạt động như thế nào:

public class Solution {

   public static void main(String[] args) {
       Graph graph = new Graph();
       graph.addVertex('A');
       graph.addVertex('B');
       graph.addVertex('C');
       graph.addVertex('D');
       graph.addVertex('E');
       graph.addVertex('F');
       graph.addVertex('G');

       graph.addEdge(0, 1, 3);
       graph.addEdge(0, 2, 5);
       graph.addEdge(0, 3, 7);
       graph.addEdge(1, 4, 6);
       graph.addEdge(2, 4, 4);
       graph.addEdge(2, 3, 3);
       graph.addEdge(3, 5, 3);
       graph.addEdge(4, 6, 6);
       graph.addEdge(5, 6, 4);

       System.out.println("The following nodes form the shortest paths from node A:");
       graph.path();
       graph.clear();
   }
}

Và đầu ra của giao diện điều khiển là thế này: Độ phức tạp về thời gian của thuật toán này không khác gì O(N2), vì chúng ta có các vòng lặp lồng nhau. Đó là tất cả những gì tôi có ngày hôm nay. Cảm ơn đã quan tâm!