Max Heap в Java

Двоичното дърво

В Java има много различни типове структури от данни. Купчината се основава на дървовидна структура, наречена двоично дърво . Двоичното дърво се състои от възли, всеки от които може да има максимум 2 дъщерни възела: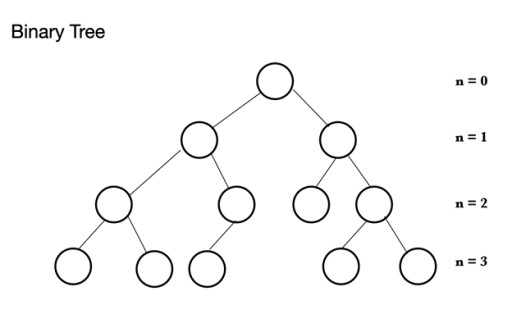 Двоичното дърво се състои от родителски възел, който може да има от 0 до 2 възела. Може да има ляв дъщерен възел и/or десен дъщерен възел, or изобщо да няма възли. В пълното двоично дърво всички възли са запълнени с изключение на последното ниво, което може да бъде пълно, но не е необходимо да бъде пълно. Последното ниво, n-то ниво, може да има от 1 до 2n възли, където първият е при n = 0 и е коренът.

Макс Хийп

Max heap (or maxheap) е пълно двоично дърво . Важното при него е, че родителският възел ТРЯБВА да има стойност, по-голяма or равна на тази на левия и десния подчинен възел. Ако това не се спазва, нямате максимален куп. Минималната купчина, от друга страна, е обратното с корена като най-малката стойност с последователни възли, нарастващи по стойност; всеки дъщерен възел има стойност, по-голяма or равна на своя родител. Освен това е пълно двоично дърво. Пример за максимална купчина е: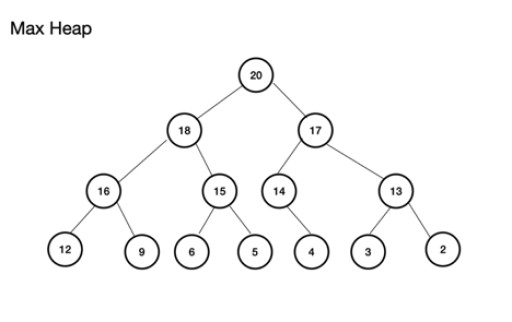 Максималната купчина може да бъде изградена от масив. Този масив ще се разглежда като дърво. За купчина, ако коренът (горният родителски възел на дървото) се съхранява на позиция (индекс) n, той се дефинира за масив, theArray , като theArray[n]. Следователно левият и десният дъщерни възли са съответно в Array[2n+1] и Array[2n+2] . За максималната купчина коренът е в Array[0] . За ниво n, корен n = 0: theArr[n] е родителският възел theArr[(2*n)+1] е левият дъщерен възел theArr[(2*n)+2] е десният дъщерен възел

Класът PriorityQueue

Купчините в Java могат да бъдат реализирани с помощта на класа PriorityQueue . PriorityQueue се използват за намиране на най- or най-малко важния елемент в колекция. Класът PriorityQueue може да бъде намерен в java.util.package . PriorityQueues трябва да се формират от обекти, които са сравними, така че да бъдат поставени в определен ред в опашката. PriorityQueue може да има компаратор, така че да се прави сравнение между обектите и опашката да се формира според това сравнение. Пример е:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Даване на изход: В този пример размерът по подразбиране на intQueue е 11, така че не е посочен (обикновено първият аргумент преди компаратора) и компараторът е даден като: Това ще направи сравнение между елементите в intQueue и ще ги сортира в дължини на масиви във възходящ ред.

Внедряване на PriorityQueue за създаване на максимална купчина

Класът PriorityQueue по подразбиране е min heap без компаратор. Минималната купчина е обратното на максималната купчина и така коренът е най-малката стойност и последователните дъщерни възли са по-големи or равни на корена и следващите родителски възли. Поради тази причина за максимална купчина е необходимо да се използва reverseOrder() от рамката на колекциите на Java като компаратор. Това ще гарантира, че ще получим максимална купчина, а не минимална купчина. Този клас има полезни методи като add() , contains() , remove() , poll() и peek() . Елементите се добавят към опашката и могат да бъдат в произволен ред. Новата опашка на PriorityQueue ще съхранява тези елементи като максимална купчина в обратен ред. Когато опашката бъде изписана, редът ще бъде: Root Left-child с root като родител (Left-child_1) Right-child с root като родител (Right-child_1) Left-child с Left-child_1 като родител (Left-child_2 ) Right-child с Left-child_1 като родител (Right-child_2) Left-child с Right-child_1 като родител (Left-child_3) Right-child с Right-child_1 като родител (Right-child_3) Left-child с Left-child_2 като родител (Left-child_4) Right-child с Left-child_2 като родител (Right-child_4) и т.н.Следният code е пример за това How се създава максимална купчина (maxheap) в java. Първото нещо, което трябва да направите, е да попълните масив със стойностите, за които ще бъде създадена максималната купчина. Това се нарича масив . След това се създава PriorityQueue , theQueue , и след това елементите от theArray се добавят към него. Това използва метода add() , напр. theQueue.add(10) за добавяне на 10 към края на опашката. За да се илюстрира част от функционалността на класа PriorityQueue , методът peek() се използва за намиране на главата на купчината и това е максималната стойност, в този случай 99. Следващата задача е да проверите размера на купчината използвайки size()което се оказва 9 и това се отпечатва на конзолата. Методът writeMaxHeap записва елементите в опашката в ред на корен, ляво дете с корен като родител, дясно дете с корен като родител, ляво дете с първо ляво дете като родител, дясно дете с първо ляво дете като родител родител, дясно-дете с първо дясно-дете като родител, ляво-дете с първо дясно-дете като родител и т.н., с последващи стойности, използващи лявото и дясното дете като родители в същия ред, Howто по-горе. Методът PriorityQueue contains(J) се използва, за да разбере дали определен елемент, J, е в опашка . В този случай търсим J = 10. В нашия пример е вярно, че това е в опашката, така че това се изписва на конзолата като вярно. След това се използва друг метод на PriorityQueue , remove(J) за премахване на J = 10 от Queue . За да се илюстрира повече от функционалността на PriorityQueue , методът poll() се използва за премахване на главния елемент (максимална стойност) с помощта на цикъл while , като всеки път премахва главния елемент в новата опашка и намалява размера на опашката с един всеки път. Това се случва в метода writeQueueизвикан от главния. Всеки път, когато премахнатият елемент се отпечатва на конзолата. Първоначалната опашка в крайна сметка няма да има останали елементи. Отпечатаните елементи са максималната купчина в низходящ ред на стойност, където главата на опашката се отпечатва всеки път.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Изход:

Макс Хепафи

Алгоритъмът Max Heapify се използва, за да се гарантира, че едно двоично дърво е максимална купчина. Ако сме във възел, n, и неговите дъщерни възли, отляво и отдясно също са максимални купчини, тогава чудесно, имаме максимална купчина. Ако това не е така в цялото дърво, тогава нямаме максимална купчина. Алгоритъмът Max Heapify се използва за сортиране на дървото, така че да се придържа към принципите на maxheap. Max Heapify работи само на един възел. Ако изискването е масивът да е max heap масив, тогава всички поддървета трябва да бъдат преобразувани в maxheap преди корена, едно по едно. Алгоритъмът трябва да се използва на всеки възел. Това ще бъде напequalsо на N/2 възли (листата ще се придържат към изискванията за максимална купчина). Времевата сложност на купчината е O(NlogN), а за един възел на височина X времевата сложност е O(X). Следният code показва How да максимизирате дърво (масив).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Даване на изход: В този code масивът се създава и запълва с числа. Създава се втори масив, newArray , и този път той ще съдържа резултата от метода, maxheapCreate , масивът с максимален обем. Методът maxHeapCreate се извиква от main и тук се създава нов масив, theNewArr , и се запълва с резултатите от maxHeapify . Това се прави чрез цикъл върху половината от размера на входния масив. За всяко преминаване на цикъла, методът maxHeapify се извиква, започвайки от елемента в средата на масива и завършвайки с първия. За всяко повикване на maxHeapify, лявото дете и дясното дете на родителския възел, i, се намират и се правят проверки, за да се намери кой е най-големият от трите, определяйки това като maxVal . Ако maxVal не е equals на родителския възел, тогава се прави суап, така че родителският възел и maxVal да се разменят и след това maxHeapify се извиква отново този път на maxVal и се извършват същите стъпки, Howто преди. В крайна сметка максималната купчина ще бъде създадена и няма да има повече итерации за извършване. Актуализираният масив, array , сега се връща към main като newArray и след това всеки следващ елемент се отпечатва на конзолата. нов масивсега е максимална купчина. Имайте предвид, че Howто в предишния пример, използвайки PriorityQueue, числата се изписват: корен, дясно-дете на корен като родител, ляво-дете на корен като родител, дясно-дете на първо дясно-дете като родител, ляво-дете на първо ляво-дете като родител, дясно-дете на първото ляво-дете като родител, ляво-дете на първото дясно-дете като родител и т.н. Те са в малко по-различен ред от тези при използване на PriorityQueue, тъй като сравнението се извършва между последователни елементи докато в примера за maxheapify, възелът се сравнява със следващите два последователни елемента в масива и се разменя за най-голямата стойност. Накратко, използват се два различни алгоритъма. И двете създават максимална купчина.

Заключение

Така че тук разгледахме максималната купчина и How тя може да бъде създадена or с PriorityQueue , or с алгоритъм Max Heapify. Използването на PriorityQueue с reverseOrder() е чист начин да направите това и препоръчителният метод. Можете обаче да изучавате тези примери и да напишете свои собствени методи, тъй като това ще бъде добро упражнение по codeиране, което ще ви помогне да успеете в интервюто си за Java Junior.