जावा में मैक्स हीप

द बाइनरी ट्री

जावा में, कई अलग-अलग प्रकार की डेटा संरचनाएँ हैं। ढेर एक पेड़ की संरचना पर आधारित है जिसे बाइनरी ट्री कहा जाता है । एक बाइनरी ट्री में नोड्स होते हैं, जिनमें से प्रत्येक में अधिकतम 2 चाइल्ड नोड हो सकते हैं: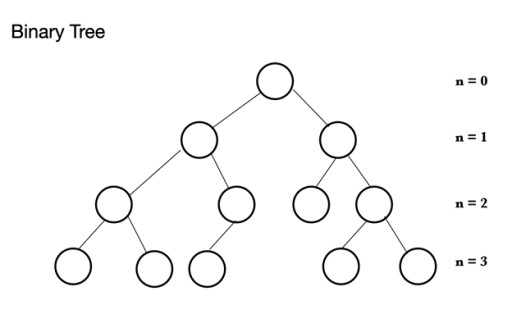 एक बाइनरी ट्री में एक पैरेंट नोड होता है जिसमें 0 से 2 नोड हो सकते हैं। इसमें लेफ्ट-चाइल्ड नोड और/या राइट-चाइल्ड नोड हो सकता है, या कोई नोड नहीं हो सकता है। एक पूर्ण बाइनरी ट्री में, अंतिम स्तर को छोड़कर सभी नोड्स भरे हुए हैं जो पूर्ण हो सकते हैं, लेकिन पूर्ण होने की आवश्यकता नहीं है। अंतिम स्तर, nवां स्तर, 1 से 2n नोड तक हो सकता है, जहां पहला n = 0 पर है और रूट है।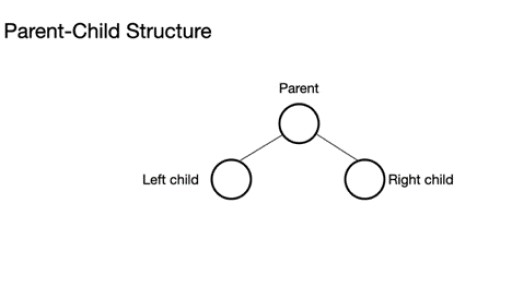

मैक्स हीप

मैक्स हीप (या मैक्सहीप) एक पूर्ण बाइनरी ट्री है । इसके बारे में महत्वपूर्ण बात यह है कि पैरेंट नोड का मान बाएँ और दाएँ-चाइल्ड नोड्स से अधिक या उसके बराबर होना चाहिए। यदि इसका पालन नहीं किया जाता है, तो आपके पास अधिकतम हीप नहीं है। दूसरी ओर, मिन हीप, रूट के विपरीत है क्योंकि मूल्य में क्रमिक नोड्स के साथ सबसे छोटा मान बढ़ रहा है; प्रत्येक बच्चे के नोड का मान उसके माता-पिता से अधिक या उसके बराबर होता है। यह एक पूर्ण बाइनरी ट्री भी है। अधिकतम हीप का एक उदाहरण है: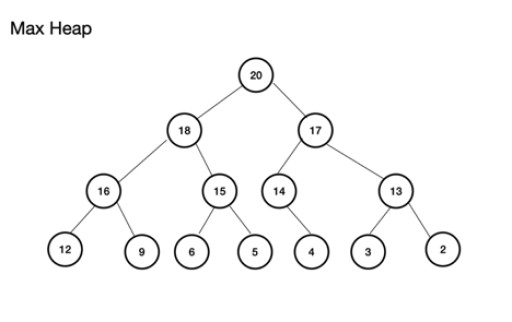 अधिकतम हीप को एक सरणी से बनाया जा सकता है। इस सरणी को एक पेड़ के रूप में माना जाएगा। ढेर के लिए, यदि रूट, (पेड़ के शीर्ष पैरेंट नोड) को स्थिति (इंडेक्स) n पर संग्रहीत किया जाता है, तो इसे सरणी के लिए परिभाषित किया जाता है, theArray , theArray[n] के रूप में. इसलिए, बाएँ और दाएँ-चाइल्ड नोड क्रमशः theArray[2n+1] और theArray[2n+2] पर हैं। अधिकतम हीप के लिए, रूट theArray[0] पर है । स्तर n के लिए, रूट n = 0: theArr[n] पैरेंट नोड है theArr[(2*n)+1] लेफ्ट चाइल्ड नोड है theArr[(2*n)+2] राइट चाइल्ड नोड है

प्रायोरिटी क्यू क्लास

जावा में ढेर को प्रायोरिटीक्यू क्लास का उपयोग करके लागू किया जा सकता है। प्रायोरिटीक्यूज़ का उपयोग संग्रह में सबसे अधिक या कम से कम महत्वपूर्ण आइटम खोजने के लिए किया जाता है। प्रायोरिटीक्यू क्लास java.util.package में पाया जा सकता है । प्रायोरिटी क्यू का निर्माण उन वस्तुओं से किया जाना चाहिए जो तुलनीय हों ताकि उन्हें कतार में एक विशेष क्रम में रखा जा सके। प्राथमिकता कतार में एक तुलनित्र हो सकता है ताकि वस्तुओं के बीच तुलना की जा सके और इस तुलना के अनुसार कतार बनाई जा सके। एक उदाहरण है:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

आउटपुट देना: इस उदाहरण में, intQueue का डिफ़ॉल्ट आकार 11 है, इसलिए यह नहीं बताया गया है (आमतौर पर तुलनित्र से पहले पहला तर्क) और तुलनित्र को इस प्रकार दिया गया है: यह intQueue में आइटम के बीच तुलना करेगा और इसे आरोही क्रम की सरणी लंबाई में सॉर्ट करेगा।

अधिकतम हीप बनाने के लिए प्रायोरिटी क्यू का कार्यान्वयन

प्रायोरिटीक्यू क्लास बिना तुलनित्र के न्यूनतम हीप के लिए डिफ़ॉल्ट है । मिन हीप अधिकतम हीप के विपरीत है और इसलिए रूट सबसे छोटा मान है और लगातार चाइल्ड नोड रूट और बाद के पैरेंटल नोड्स के बराबर या बड़े होते हैं। इस कारण से, अधिकतम हीप के लिए, जावा के कलेक्शंस फ्रेमवर्क से तुलनित्र के रूप में रिवर्सऑर्डर () का उपयोग करना आवश्यक है । यह सुनिश्चित करेगा कि हमें अधिकतम हीप मिले न कि न्यूनतम हीप। इस क्लास में ऐड () , सम्‍मिलित () , रिमूव () , पोल () , और पीक () जैसी उपयोगी विधियाँ हैं । तत्वों को कतार में जोड़ा जाता है और वे किसी भी क्रम में हो सकते हैं। नई प्रायोरिटी क्यू कतार उन तत्वों को उल्टे क्रम में अधिकतम हीप के रूप में संग्रहीत करेगी। जब कतार लिखी जाती है, तो क्रम होगा: रूट लेफ्ट-चाइल्ड रूट के साथ पैरेंट (लेफ्ट-चाइल्ड_1) राइट-चाइल्ड विद रूट पैरेंट के रूप में (राइट-चाइल्ड_1) लेफ्ट-चाइल्ड विद लेफ्ट-चाइल्ड_1 पैरेंट के रूप में (लेफ्ट-चाइल्ड_2) ) राइट-चाइल्ड विद लेफ्ट-चाइल्ड_1 माता-पिता के रूप में (राइट-चाइल्ड_2) लेफ्ट-चाइल्ड विथ राइट-चाइल्ड_1 पैरेंट के रूप में (लेफ्ट-चाइल्ड_3) राइट-चाइल्ड विथ राइट-चाइल्ड_1 माता-पिता के रूप में (राइट-चाइल्ड_3) लेफ्ट-चाइल्ड विथ लेफ्ट-चाइल्ड_2 माता-पिता के रूप में (लेफ्ट-चाइल्ड_4) राइट-चाइल्ड विथ लेफ्ट-चाइल्ड_2 पैरेंट के रूप में (राइट-चाइल्ड_4), आदि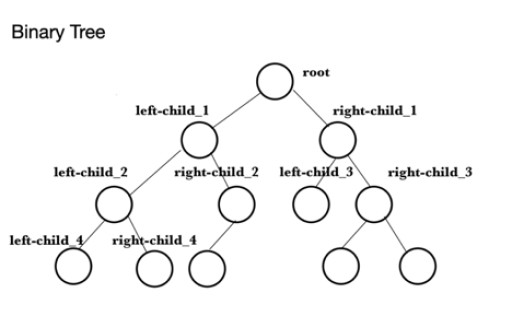निम्नलिखित कोड एक उदाहरण है कि जावा में अधिकतम ढेर (मैक्सहेप) कैसे बनाया जाता है। करने के लिए पहली बात यह है कि एक सरणी को उन मानों से भरना है जिनके लिए अधिकतम ढेर बनाया जाएगा। इसे ऐरे कहा जाता है । इसके बाद, एक प्रायोरिटी क्यू , द क्यू , बनाया जाता है और फिर ऐरे के तत्वों को इसमें जोड़ा जाता है। यह कतार के अंत में 10 जोड़ने के लिए ऐड() विधि का उपयोग करता है , उदाहरण के लिए theQueue.add(10) । प्रायोरिटीक्यू क्लास की कुछ कार्यक्षमता को स्पष्ट करने के लिए , विधि पीक () का उपयोग तब हीप के प्रमुख को खोजने के लिए किया जाता है, और यह अधिकतम मूल्य है, इस मामले में, 99। अगला कार्य हीप के आकार की जांच करना है आकार का उपयोग ()जो 9 पाया जाता है और इसे कंसोल पर प्रिंट किया जाता है। विधि राइटमैक्सहीप रूट के क्रम में कतार में तत्वों को लिखता है, माता-पिता के रूप में रूट के साथ बाएं-बच्चे, माता-पिता के रूप में रूट के साथ दाएं-बच्चे, माता-पिता के रूप में पहले बाएं-बच्चे के साथ बाएं-बच्चे, पहले बाएं-बच्चे के साथ दाएं-बच्चे के रूप में माता-पिता, माता-पिता के रूप में पहले दाएं-बच्चे के साथ दाएं-बच्चे, माता-पिता के रूप में पहले दाएं-बच्चे के साथ बाएं-बच्चे आदि, ऊपर के क्रम में माता-पिता के रूप में बाएं और दाएं बच्चों का उपयोग करने वाले बाद के मूल्यों के साथ। प्राथमिकता क्यू विधि में शामिल है (जे) यह पता लगाने के लिए प्रयोग किया जाता है कि एक विशिष्ट तत्व, जे, कतार में है या नहीं। इस मामले में हम J = 10 की तलाश करते हैं। हमारे उदाहरण में, यह सच है कि यह कतार में है इसलिए इसे कंसोल पर सत्य के रूप में लिखा जाता है। एक और प्रायोरिटी क्यू मेथड, रिमूव (जे) का उपयोग क्यू से जे = 10 को हटाने के लिए किया जाता है । प्रायोरिटीक्यू की कार्यक्षमता को और अधिक स्पष्ट करने के लिए , मेथड पोल () का उपयोग हेड एलिमेंट (अधिकतम मान) को हटाने के लिए किया जाता है , हर बार नई क्यू में हेड एलिमेंट को हटाते हुए और हर बार क्यू को आकार में घटाते हुए। यह मेथड राइट क्यू में होता हैमुख्य से बुलाया गया। हर बार हटाए गए तत्व को कंसोल पर प्रिंट किया जाता है। मूल कतार में अंततः कोई तत्व नहीं बचेगा। मुद्रित तत्व मूल्य के अवरोही क्रम में अधिकतम हीप हैं, जहां कतार के प्रमुख को हर बार प्रिंट किया जाता है।

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

आउटपुट:

मैक्स हेपिफाय

Max Heapify एल्गोरिथ्म का उपयोग यह सुनिश्चित करने के लिए किया जाता है कि बाइनरी ट्री अधिकतम हीप है। यदि हम एक नोड पर हैं, n, और उसके बच्चे के नोड्स, बाएँ और दाएँ भी स्वयं अधिकतम ढेर हैं, तो महान, हमारे पास अधिकतम ढेर है। यदि पूरे पेड़ में ऐसा नहीं है तो हमारे पास अधिकतम हीप नहीं है। Max Heapify एल्गोरिथम का उपयोग ट्री को सॉर्ट करने के लिए किया जाता है ताकि यह maxheap सिद्धांतों का पालन करे। Max Heapify केवल एक नोड पर काम करता है। यदि आवश्यकता यह है कि सरणी एक अधिकतम हीप सरणी है, तो सभी उप पेड़ों को रूट से पहले, एक समय में मैक्सहेप में परिवर्तित किया जाना चाहिए। प्रत्येक नोड पर एल्गोरिदम का उपयोग किया जाना चाहिए। यह एन/2 नोड्स पर किया जाएगा (पत्तियां अधिकतम हीप आवश्यकताओं का पालन करेंगी)। हीप की समय जटिलता O(NlogN) है, और ऊंचाई X पर एक नोड के लिए, समय जटिलता O(X) है। निम्न कोड दिखाता है कि एक पेड़ (एक सरणी) को अधिकतम कैसे करें।

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

आउटपुट देना: इस कोड में, ऐरे बनाया जाता है और संख्याओं से भरा जाता है। एक दूसरी सरणी, newArray बनाई जाती है और इस बार इसमें विधि का परिणाम होगा, maxheapCreate , अधिकतम हीप सरणी। विधि maxHeapCreate को main से कॉल किया जाता है , और यहाँ एक नई सरणी, theNewArr , बनाई जाती है और maxHeapify परिणामों से भरी जाती है। यह इनपुट ऐरे के आधे से अधिक आकार को लूप करके किया जाता है। लूप के प्रत्येक पास के लिए, विधि maxHeapify को एरे के बीच में तत्व से शुरू करके पहले के साथ समाप्त कहा जाता है। MaxHeapify की प्रत्येक कॉल के लिए, माता-पिता नोड के बाएं बच्चे और दाएं बच्चे, i, पाए जाते हैं और यह पता लगाने के लिए जांच की जाती है कि तीनों में से सबसे बड़ा कौन सा है, जो कि maxVal के रूप में परिभाषित करता है । यदि maxVal पैरेंट नोड के बराबर नहीं है, तो एक स्वैप किया जाता है ताकि पैरेंट नोड और maxVal की अदला-बदली हो और फिर maxHeapify को इस बार फिर से maxVal पर बुलाया जाए और पहले की तरह ही कदम उठाए जाएं। अंतत: अधिकतम हीप बनाया जाएगा और आगे ले जाने के लिए कोई पुनरावृति नहीं होगी। अद्यतन सरणी, सरणी , अब मुख्य रूप से newArray के रूप में वापस आ गई है और फिर प्रत्येक लगातार तत्व कंसोल पर मुद्रित किया गया है। newArrayअब एक अधिकतम ढेर है। ध्यान दें, जैसा कि पिछले उदाहरण में प्रायोरिटीक्यू का उपयोग करके संख्याएँ लिखी जाती हैं: रूट, पैरेंट के रूप में रूट का राइट-चाइल्ड, पैरेंट के रूप में रूट का लेफ्ट-चाइल्ड, पैरेंट के रूप में पहले राइट-चाइल्ड का राइट-चाइल्ड, पहले का लेफ्ट-चाइल्ड माता-पिता के रूप में बाएँ-बच्चे, माता-पिता के रूप में पहले बाएँ-बच्चे का दाएँ-बच्चा, माता-पिता के रूप में पहले दाएँ-बच्चे का बायाँ-बच्चा, आदि। प्रायोरिटीक्यू का उपयोग करते समय वे थोड़े अलग क्रम में होते हैं क्योंकि तुलना लगातार तत्वों के बीच की जाती है जबकि maxheapify उदाहरण में, नोड की तुलना सरणी में अगले दो क्रमिक तत्वों से की जाती है और सबसे बड़े मान के लिए अदला-बदली की जाती है। संक्षेप में, दो अलग-अलग एल्गोरिदम का उपयोग किया जाता है। दोनों अधिकतम ढेर बनाते हैं।

निष्कर्ष

इसलिए यहां हमने मैक्स हीप पर ध्यान दिया है और इसे प्रायोरिटीक्यू या मैक्स हीपिफाय एल्गोरिथम के साथ कैसे बनाया जा सकता है। प्रायोरिटी क्यू का उपयोग रिवर्सऑर्डर () के साथ करना ऐसा करने का एक अच्छा तरीका है और अनुशंसित विधि है। हालाँकि, आप इन उदाहरणों का अध्ययन कर सकते हैं और अपने तरीके लिख सकते हैं क्योंकि यह एक अच्छा कोडिंग अभ्यास होगा जो जावा जूनियर के लिए आपके साक्षात्कार में सफल होने में आपकी मदद करेगा।