Max Heap in Java

De binaire boom

In Java zijn er veel verschillende soorten datastructuren. De heap is gebaseerd op een boomstructuur die een binaire boom wordt genoemd . Een binaire boom bestaat uit knooppunten, die elk maximaal 2 onderliggende knooppunten kunnen hebben: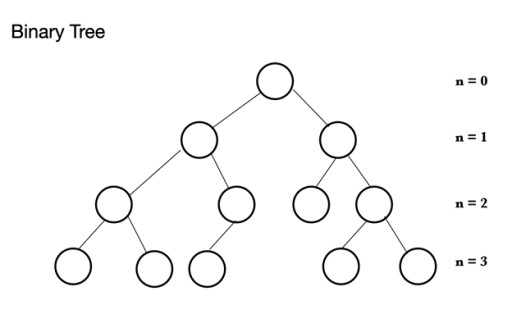 Een binaire boom bestaat uit een bovenliggend knooppunt dat 0 tot 2 knooppunten kan hebben. Het kan een linkerkindknooppunt en/of een rechterkindknooppunt hebben, of helemaal geen knooppunten. In een volledige binaire boom zijn alle knooppunten gevuld behalve het laatste niveau dat vol kan zijn, maar dat hoeft niet vol te zijn. Het laatste niveau, het n-de niveau, kan 1 tot 2n knooppunten hebben, waarbij de eerste op n = 0 staat en de wortel is.

Maximale hoop

Max heap (of maxheap) is een complete binaire boom . Het belangrijkste hiervan is dat het bovenliggende knooppunt een waarde MOET hebben die groter is dan of gelijk is aan die van de linker- en rechterkindknooppunten. Als je je hier niet aan houdt, heb je geen max heap. Min heap, aan de andere kant, is het tegenovergestelde met de root als de kleinste waarde met opeenvolgende knooppunten die in waarde toenemen; elk onderliggend knooppunt heeft een waarde die groter is dan of gelijk is aan die van het bovenliggende knooppunt. Het is ook een complete binaire boom. Een voorbeeld van een max heap is: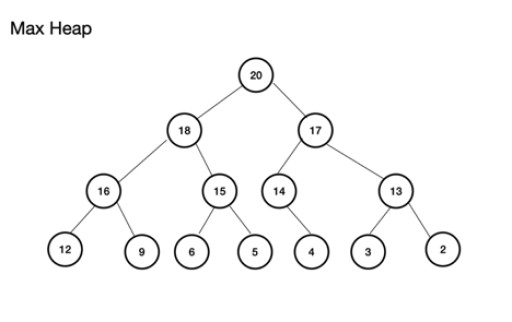 Max heap kan worden opgebouwd uit een array. Deze array zal worden gezien in termen van een boom. Als voor een heap de root (bovenste bovenliggende node van de boom) wordt opgeslagen op positie (index) n, wordt deze voor array, theArray , gedefinieerd als theArray[n]. De linker- en rechterkindknooppunten bevinden zich daarom respectievelijk in theArray[2n+1] en theArray[2n+2] . Voor de maximale heap bevindt de root zich in theArray[0] . Voor het niveau n, root n = 0: theArr[n] is het bovenliggende knooppunt theArr[(2*n)+1] is het linker onderliggende knooppunt theArr[(2*n)+2] is het rechter onderliggende knooppunt

De PriorityQueue-klasse

Heaps in Java kunnen worden geïmplementeerd met behulp van de PriorityQueue Class. PriorityQueues worden gebruikt om het meest of minst belangrijke item in een verzameling te vinden. De klasse PriorityQueue is te vinden in het java.util.package . PriorityQueues moeten worden gevormd uit objecten die vergelijkbaar zijn, zodat ze in een bepaalde volgorde in de wachtrij worden geplaatst. PriorityQueue kan een comparator hebben zodat een vergelijking tussen de objecten wordt gemaakt en de wachtrij wordt gevormd op basis van deze vergelijking. Een voorbeeld is:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Uitvoer geven: In dit voorbeeld is de standaardgrootte van intQueue 11, dus deze is niet vermeld (meestal het eerste argument vóór de comparator) en de comparator is gegeven als: Dit zal een vergelijking maken tussen de items in intQueue en deze sorteren in reekslengtes van oplopende volgorde.

Implementatie van PriorityQueue om een ​​maximale heap te creëren

De PriorityQueue Class is standaard ingesteld op min heap zonder comparator. Min heap is het tegenovergestelde van max heap en dus is de wortel de kleinste waarde en zijn opeenvolgende onderliggende knooppunten groter of gelijk aan de wortel en daaropvolgende ouderlijke knooppunten. Om deze reden is het voor max heap noodzakelijk om reverseOrder() uit Java's Collections-framework als vergelijker te gebruiken. Dit zorgt ervoor dat we een maximale heap krijgen en niet een minimale heap. Deze klasse heeft handige methoden zoals add() , contain() , remove() , poll() en peek() . Elementen worden aan de wachtrij toegevoegd en kunnen in willekeurige volgorde staan. De nieuwe PriorityQueue-wachtrij slaat die elementen op als een maximale heap in omgekeerde volgorde. Wanneer de wachtrij is uitgeschreven, is de volgorde: Root Linkerkind met root als parent (Left-child_1) Right-child met root als parent (Right-child_1) Left-child met Left-child_1 als parent (Left-child_2 ) Rechterkind met Linkerkind_1 als ouder (Rechtskind_2) Linkerkind met Rechterkind_1 als ouder (Linkerkind_3) Rechterkind met Rechterkind_1 als ouder (Rechtskind_3) Linkerkind met Linkerkind_2 als ouder (Left-child_4) Right-child met Left-child_2 als parent (Right-child_4), etcDe volgende code is een voorbeeld van hoe een maximale heap (maxheap) wordt gemaakt in Java. Het eerste dat u moet doen, is een array vullen met de waarden waarvoor de maximale heap wordt gemaakt. Dit wordt deArray genoemd . Vervolgens wordt een PriorityQueue , theQueue , aangemaakt en vervolgens worden de elementen uit theArray hieraan toegevoegd. Dit gebruikt de methode add() , bijv. theQueue.add(10) om 10 toe te voegen aan het einde van de wachtrij. Om een ​​deel van de functionaliteit van de klasse PriorityQueue te illustreren , wordt de methode peek() vervolgens gebruikt om de kop van de heap te vinden, en dit is de maximale waarde, in dit geval 99. De volgende taak is het controleren van de grootte van de heap grootte() gebruikendat blijkt 9 te zijn en dit wordt afgedrukt op de console. Methode writeMaxHeap schrijft de elementen in de wachtrij weg in de volgorde root, linkerkind met root als ouder, rechterkind met root als ouder, linkerkind met eerste linkerkind als ouder, rechterkind met eerste linkerkind als parent, right-child met first right-child als parent, left-child met first right-child als parent enz., waarbij de volgende waarden de linker- en rechterkinderen als ouders gebruiken in dezelfde volgorde als hierboven. De PriorityQueue- methode bevat(J) wordt gebruikt om erachter te komen of een specifiek element, J, in een wachtrij staat. In dit geval zoeken we naar J = 10. In ons voorbeeld is het waar dat dit in de wachtrij staat, dus dit wordt als waar naar de console geschreven. Een andere PriorityQueue- methode, remove(J) wordt vervolgens gebruikt om J = 10 uit theQueue te verwijderen . Om meer van de functionaliteit van PriorityQueue te illustreren , wordt de methode poll() gebruikt om het head-element (maximale waarde) te verwijderen met behulp van een while- lus, waarbij telkens het head-element in de nieuwe wachtrij wordt verwijderd en de wachtrij telkens met één wordt verkleind. Dit gebeurt in de methode writeQueuegebeld van hoofd. Elke keer dat het verwijderde element naar de console wordt afgedrukt. De oorspronkelijke wachtrij zal uiteindelijk geen elementen meer bevatten. De afgedrukte elementen zijn de maximale stapel in aflopende volgorde van waarde, waarbij de kop van de wachtrij elke keer wordt afgedrukt.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Uitgang:

Max Heapify

Het Max Heapify-algoritme wordt gebruikt om ervoor te zorgen dat een binaire boom een ​​maximale heap is. Als we ons op een knooppunt bevinden, n, en zijn onderliggende knooppunten, links en rechts zijn zelf ook maximale hopen, dan hebben we een maximale hoop. Als dit niet in de hele boom het geval is, hebben we geen maximale hoop. Het Max Heapify-algoritme wordt gebruikt om de boom zo te sorteren dat deze voldoet aan de maxheap-principes. Max Heapify werkt op slechts één knooppunt. Als de vereiste is dat de array een max heap-array is, moeten alle substructuren één voor één worden geconverteerd naar maxheap vóór de root. Het algoritme moet op elk knooppunt worden gebruikt. Dit wordt gedaan op N/2 nodes (leaves voldoen aan de maximale heapvereisten). De tijdcomplexiteit van de heap is O(NlogN), en voor één knooppunt op hoogte X is de tijdcomplexiteit O(X). De volgende code laat zien hoe je een boom (een array) maxheapify maakt.

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Uitvoer geven: In deze code wordt theArray gemaakt en gevuld met getallen. Er wordt een tweede array, newArray , gemaakt en deze keer bevat deze het resultaat van de methode maxheapCreate , de max heap-array. Methode maxHeapCreate wordt aangeroepen vanuit main , en hier wordt een nieuwe array, theNewArr , gemaakt en gevuld met de maxHeapify- resultaten. Dit wordt gedaan door meer dan de helft van de grootte van de invoerarray te herhalen. Voor elke doorgang van de lus wordt de methode maxHeapify aangeroepen, beginnend bij het element in het midden van de array en eindigend bij het eerste. Voor elke aanroep van maxHeapify, het linkerkind en het rechterkind van het bovenliggende knooppunt, i, worden gevonden en er worden controles uitgevoerd om te bepalen welke de grootste van de drie is, waarbij dat wordt gedefinieerd als maxVal . Als maxVal niet gelijk is aan het bovenliggende knooppunt, wordt er gewisseld zodat het bovenliggende knooppunt en maxVal worden verwisseld en wordt maxHeapify deze keer opnieuw aangeroepen op maxVal en worden dezelfde stappen uitgevoerd als voorheen. Uiteindelijk zal de maximale heap worden gemaakt en zijn er geen iteraties meer om uit te voeren. De bijgewerkte array, array , wordt nu teruggestuurd naar main als newArray en vervolgens wordt elk opeenvolgend element afgedrukt naar de console. nieuweArrayis nu een maximale hoop. Merk op dat, net als in het vorige voorbeeld met PriorityQueue, de getallen worden uitgeschreven: wortel, rechterkind van wortel als ouder, linkerkind van wortel als ouder, rechterkind van eerste rechterkind als ouder, linkerkind van eerste linkerkind als ouder, rechterkind van eerste linkerkind als ouder, linkerkind van eerste rechterkind als ouder, enz. Ze staan ​​in een iets andere volgorde dan bij gebruik van PriorityQueue omdat de vergelijking wordt gemaakt tussen opeenvolgende elementen terwijl in het maxheapify-voorbeeld het knooppunt wordt vergeleken met de volgende twee opeenvolgende elementen in de array en wordt verwisseld voor de grootste waarde. Kortom, er worden twee verschillende algoritmen gebruikt. Beide creëren een maximale heap.

Conclusie

Dus hier hebben we gekeken naar max heap en hoe deze kan worden gemaakt met een PriorityQueue of een Max Heapify-algoritme. Het gebruik van de PriorityQueue met reverseOrder() is een handige manier om dit te doen en de aanbevolen methode. U kunt deze voorbeelden echter bestuderen en uw eigen methoden schrijven, aangezien dit een goede codeeroefening zal zijn die u zal helpen slagen in uw sollicitatiegesprek voor Java Junior.