ஜாவாவில் மேக்ஸ் ஹீப்

பைனரி மரம்

ஜாவாவில், பல்வேறு வகையான தரவு கட்டமைப்புகள் உள்ளன. குவியல் பைனரி மரம் எனப்படும் மர அமைப்பை அடிப்படையாகக் கொண்டது . ஒரு பைனரி மரம் முனைகளைக் கொண்டுள்ளது, அவை ஒவ்வொன்றும் அதிகபட்சமாக 2 குழந்தை முனைகளைக் கொண்டிருக்கலாம்: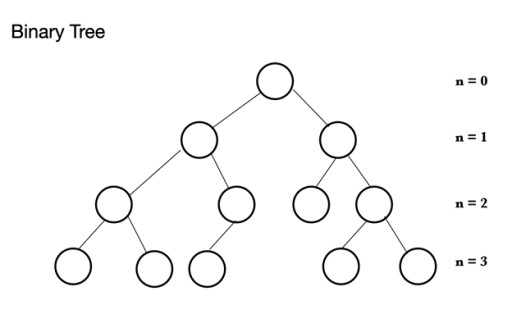 ஒரு பைனரி மரம் 0 முதல் 2 முனைகளைக் கொண்டிருக்கும் ஒரு பெற்றோர் முனையைக் கொண்டுள்ளது. இது இடது-குழந்தை முனை மற்றும்/அல்லது வலது-குழந்தை முனை அல்லது முனைகள் இல்லாமல் இருக்கலாம். ஒரு முழுமையான பைனரி மரத்தில், நிரம்பிய கடைசி நிலை தவிர அனைத்து முனைகளும் நிரப்பப்படும், ஆனால் முழுதாக இருக்க வேண்டிய அவசியமில்லை. கடைசி நிலை, n வது நிலை, 1 முதல் 2n வரையிலான முனைகளைக் கொண்டிருக்கலாம், இதில் முதலாவது n = 0 மற்றும் ரூட் ஆகும்.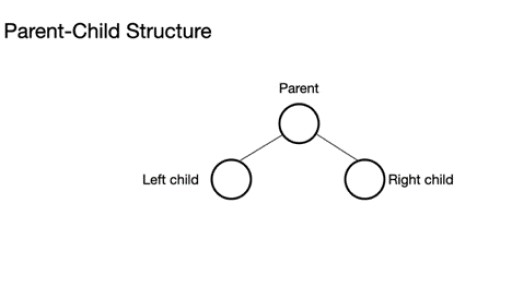

அதிகபட்ச குவியல்

மேக்ஸ் ஹீப் (அல்லது மேக்ஸ்ஹீப்) ஒரு முழுமையான பைனரி மரம் . இதில் முக்கியமான விஷயம் என்னவென்றால், பெற்றோர் முனை இடது மற்றும் வலது குழந்தை முனைகளின் மதிப்பை விட அதிகமாகவோ அல்லது அதற்கு சமமாகவோ இருக்க வேண்டும். இது கடைபிடிக்கப்படாவிட்டால், உங்களிடம் அதிகபட்ச குவியல் இல்லை. Min heap, மறுபுறம், மதிப்பு அதிகரிப்பதன் மூலம் அடுத்தடுத்த முனைகளுடன் மிகச்சிறிய மதிப்பாக ரூட்டுடன் எதிர் உள்ளது; ஒவ்வொரு குழந்தை முனையும் அதன் பெற்றோரை விட அதிகமாக அல்லது அதற்கு சமமான மதிப்பைக் கொண்டுள்ளது. இது ஒரு முழுமையான பைனரி மரமாகவும் உள்ளது. அதிகபட்சக் குவியலின் உதாரணம்: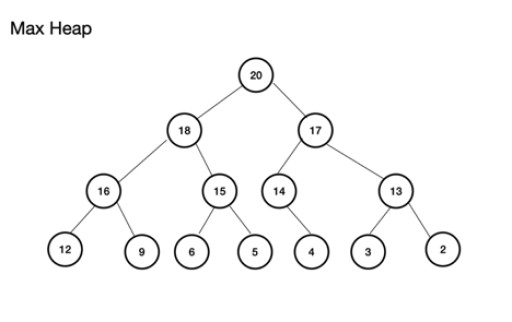 அதிகபட்சக் குவியலை ஒரு வரிசையிலிருந்து உருவாக்கலாம். இந்த வரிசை ஒரு மரத்தின் அடிப்படையில் கருதப்படுகிறது. ஒரு குவியலுக்கு, வேர், (மரத்தின் மேல் பெற்றோர் முனை) நிலை (குறியீட்டு) n இல் சேமிக்கப்பட்டால், அது வரிசை, theArray க்கு , theArray[n] என வரையறுக்கப்படுகிறது.. எனவே, இடது மற்றும் வலது குழந்தை முனைகள் முறையே வரிசை[2n+1] மற்றும் வரிசை[2n+2] இல் உள்ளன. அதிகபட்ச குவியலுக்கு, ரூட் theArray[0] இல் உள்ளது . n நிலைக்கு, ரூட் n = 0: theArr[n] என்பது பெற்றோர் முனை ஆகும், இது Arr[(2*n)+1] என்பது இடது குழந்தை முனை ஆகும், இது Arr[(2*n)+2] என்பது வலது குழந்தை முனை ஆகும்.

முன்னுரிமை வரிசை வகுப்பு

ஜாவாவில் உள்ள குவியல்களை முன்னுரிமை வரிசை வகுப்பைப் பயன்படுத்தி செயல்படுத்தலாம் . ஒரு சேகரிப்பில் உள்ள மிக முக்கியமான அல்லது குறைந்த முக்கியப் பொருளைக் கண்டறிய முன்னுரிமை வரிசைகள் பயன்படுத்தப்படுகின்றன. PriorityQueue வகுப்பை java.util.package இல் காணலாம் . முன்னுரிமை வரிசைகள் ஒப்பிடக்கூடிய பொருட்களால் உருவாக்கப்பட வேண்டும், இதனால் அவை வரிசையில் ஒரு குறிப்பிட்ட வரிசையில் வைக்கப்படும். PriorityQueue ஒரு ஒப்பீட்டாளரைக் கொண்டிருக்கலாம், இதனால் பொருள்களுக்கு இடையே ஒரு ஒப்பீடு செய்யப்படுகிறது மற்றும் இந்த ஒப்பீட்டின் படி வரிசை உருவாகிறது. ஒரு உதாரணம்:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

வெளியீடு கொடுக்கிறது: இந்த எடுத்துக்காட்டில், intQueue இன் இயல்புநிலை அளவு 11 ஆகும், எனவே குறிப்பிடப்படவில்லை (பொதுவாக ஒப்பீட்டாளருக்கு முன் முதல் வாதம்) மற்றும் ஒப்பீட்டாளர் இவ்வாறு கொடுக்கப்பட்டுள்ளது: இது intQueue இல் உள்ள உருப்படிகளை ஒப்பிட்டு , ஏறுவரிசையின் வரிசை நீளமாக வரிசைப்படுத்தும்.

அதிகபட்ச குவியலை உருவாக்க முன்னுரிமை வரிசையை செயல்படுத்துதல்

PriorityQueue Class ஆனது ஒப்பீட்டாளர் இல்லாமல் min heapக்கு இயல்புநிலையாக இருக்கும். Min heap என்பது அதிகபட்சக் குவியலுக்கு எதிரானது, எனவே ரூட் என்பது மிகச் சிறிய மதிப்பு மற்றும் அடுத்தடுத்த குழந்தை முனைகள் பெரியதாகவோ அல்லது ரூட் மற்றும் அடுத்தடுத்த பெற்றோர் முனைகளுக்கு சமமாகவோ இருக்கும். இந்த காரணத்திற்காக, அதிகபட்ச குவியலுக்கு, ஜாவாவின் சேகரிப்பு கட்டமைப்பிலிருந்து reverseOrder()ஐ ஒப்பீட்டாளராகப் பயன்படுத்துவது அவசியம் . இது அதிகபட்சக் குவியலைப் பெறுவதை உறுதி செய்யும், ஒரு நிமிடக் குவியலை அல்ல. இந்த வகுப்பில் add() , contains() , remove() , poll() , and peek() போன்ற பயனுள்ள முறைகள் உள்ளன . கூறுகள் வரிசையில் சேர்க்கப்படுகின்றன மற்றும் எந்த வரிசையிலும் இருக்கலாம். புதிய PriorityQueue வரிசை அந்த உறுப்புகளை தலைகீழ் வரிசையில் அதிகபட்ச குவியலாக சேமிக்கும். வரிசையை எழுதும் போது, ​​வரிசை: ரூட் இடது-குழந்தை பெற்றோராக ரூட் (இடது-குழந்தை_1) வலது-குழந்தை பெற்றோராக மூலத்துடன் (வலது-குழந்தை_1) இடது-குழந்தை இடது-குழந்தை_1 பெற்றோராக (இடது-குழந்தை_2 ) வலது-குழந்தையுடன் இடது-குழந்தை_1 பெற்றோராக (வலது-குழந்தை_2) இடது-குழந்தை வலது-குழந்தை_1 பெற்றோராக (இடது-குழந்தை_3) வலது-குழந்தையுடன் வலது-குழந்தை_1 பெற்றோராக பெற்றோராக (இடது-குழந்தை_4) வலது-குழந்தையுடன் இடது-குழந்தை_2 பெற்றோராக (வலது-குழந்தை_4) போன்றவை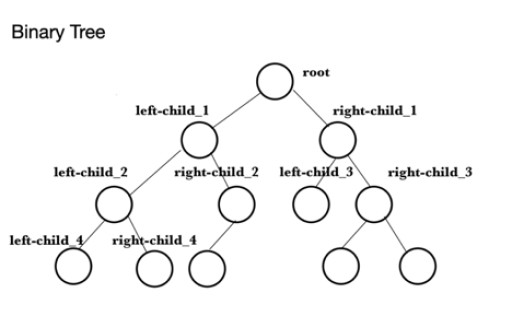ஜாவாவில் அதிகபட்சக் குவியல் (maxheap) எவ்வாறு உருவாக்கப்படுகிறது என்பதற்கு பின்வரும் குறியீடு ஒரு எடுத்துக்காட்டு. முதலில் செய்ய வேண்டியது, அதிகபட்ச குவியல் உருவாக்கப்படும் மதிப்புகளுடன் ஒரு வரிசையை நிரப்ப வேண்டும். இது வரிசை என்று அழைக்கப்படுகிறது . அடுத்து, ஒரு PriorityQueue , theQueue , உருவாக்கப்பட்டு பின்னர் theArray இலிருந்து கூறுகள் இதில் சேர்க்கப்படும். இது வரிசையின் முடிவில் 10 ஐ சேர்க்க add() , எடுத்துக்காட்டாக theQueue.add(10) முறையைப் பயன்படுத்துகிறது . PriorityQueue Class ன் சில செயல்பாடுகளை விளக்குவதற்கு , குவியல்களின் தலையைக் கண்டறிய முறை peek() பயன்படுத்தப்படுகிறது, மேலும் இதுவே அதிகபட்ச மதிப்பாகும், இந்த விஷயத்தில், 99. அடுத்த பணி குவியல் அளவை சரிபார்க்க வேண்டும். அளவைப் பயன்படுத்தி ()இது 9 ஆகக் கண்டறியப்பட்டது, இது கன்சோலில் அச்சிடப்படுகிறது. முறை writeMaxHeap வரிசையில் உள்ள உறுப்புகளை ரூட், இடது-குழந்தை பெற்றோராக ரூட், வலது-குழந்தை பெற்றோராக ரூட், இடது-குழந்தை முதல் இடது-குழந்தை பெற்றோராக, வலது-குழந்தை முதல் இடது-குழந்தை என வரிசையில் எழுதுகிறது. பெற்றோர், வலது-குழந்தை முதல் வலது-குழந்தை பெற்றோராக, இடது-குழந்தை முதல் வலது-குழந்தை பெற்றோர் போன்றவை, அடுத்தடுத்த மதிப்புகளுடன் இடது மற்றும் வலது குழந்தைகளை பெற்றோராக மேலே உள்ள அதே வரிசையில் பயன்படுத்துகிறது. PriorityQueue முறை கொண்டுள்ளது(J) என்பது ஒரு குறிப்பிட்ட உறுப்பு, J, வரிசையில் உள்ளதா என்பதைக் கண்டறிய பயன்படுகிறது . இந்த வழக்கில் நாம் J = 10 ஐத் தேடுகிறோம். எங்கள் எடுத்துக்காட்டில், இது வரிசையில் உள்ளது என்பது உண்மைதான், எனவே இது கன்சோலில் உண்மை என எழுதப்பட்டது. மற்றொரு முன்னுரிமை வரிசை முறை, வரிசையிலிருந்து J = 10 ஐ அகற்ற, remove(J) பயன்படுத்தப்படுகிறது . PriorityQueue இன் செயல்பாடுகளை மேலும் விளக்குவதற்கு , ஒரு வேளை லூப்பைப் பயன்படுத்தி ஹெட் உறுப்பை (அதிகபட்ச மதிப்பு) அகற்ற முறை கருத்துக் கணிப்பு() பயன்படுகிறது , ஒவ்வொரு முறையும் புதிய வரிசையில் உள்ள ஹெட் உறுப்பை அகற்றி, ஒவ்வொரு முறையும் வரிசையின் அளவைக் குறைக்கவும். இது ரைட் க்யூ முறையில் நடக்கும்முக்கியமாக இருந்து அழைக்கப்பட்டது. ஒவ்வொரு முறையும் அகற்றப்பட்ட உறுப்பு கன்சோலில் அச்சிடப்படும். அசல் வரிசையில் இறுதியில் கூறுகள் எதுவும் இருக்காது. அச்சிடப்பட்ட கூறுகள் மதிப்பின் இறங்கு வரிசையில் அதிகபட்ச குவியலாகும், அங்கு ஒவ்வொரு முறையும் வரிசையின் தலை அச்சிடப்படும்.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

வெளியீடு:

அதிகபட்ச Heapify

பைனரி மரம் ஒரு அதிகபட்ச குவியலாக இருப்பதை உறுதி செய்ய Max Heapify வழிமுறை பயன்படுத்தப்படுகிறது. நாம் ஒரு முனையில் இருந்தால், n, மற்றும் அதன் குழந்தை முனைகள், இடது மற்றும் வலது கூட அதிகபட்ச குவியல்களாக இருந்தால், பெரியது, நமக்கு அதிகபட்ச குவியல் உள்ளது. மரம் முழுவதும் இப்படி இல்லை என்றால் நம்மிடம் அதிகபட்ச குவியல் இல்லை. Max Heapify அல்காரிதம் மரத்தை வரிசைப்படுத்த பயன்படுகிறது, அதனால் அது maxheap கொள்கைகளை கடைபிடிக்கிறது. Max Heapify ஒரே ஒரு முனையில் வேலை செய்கிறது. வரிசையானது அதிகபட்சக் குவியலாக இருக்க வேண்டுமெனில், அனைத்து துணை மரங்களும் வேருக்கு முன் மேக்ஸ்ஹீப் ஆக மாற்றப்பட வேண்டும். அல்காரிதம் ஒவ்வொரு முனையிலும் பயன்படுத்தப்பட வேண்டும். இது N/2 முனைகளில் செய்யப்படும் (இலைகள் அதிகபட்ச குவியல் தேவைகளை கடைபிடிக்கும்). குவியலின் நேர சிக்கலானது O(NlogN), மற்றும் உயரம் X இல் உள்ள ஒரு முனைக்கு, நேர சிக்கலானது O(X) ஆகும். பின்வரும் குறியீடு ஒரு மரத்தை (வரிசை) எவ்வாறு அதிகப்படுத்துவது என்பதைக் காட்டுகிறது.

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

வெளியீடு கொடுக்கிறது: இந்த குறியீட்டில், theArray உருவாக்கப்பட்டு எண்களால் நிரப்பப்படுகிறது. இரண்டாவது வரிசை, newArray உருவாக்கப்பட்டது, இந்த முறை அது maxheapCreate , max heap array என்ற முறையின் முடிவைக் கொண்டிருக்கும். maxHeapCreate மெயின் இலிருந்து அழைக்கப்படுகிறது , மேலும் இங்கே ஒரு புதிய வரிசை, theNewArr உருவாக்கப்பட்டது மற்றும் maxHeapify முடிவுகளால் நிரப்பப்படுகிறது. உள்ளீட்டு வரிசையின் பாதி அளவைக் கொண்டு இது செய்யப்படுகிறது. லூப்பின் ஒவ்வொரு பாஸுக்கும், முறை maxHeapify , அணிவரிசையின் நடுவில் உள்ள உறுப்பில் தொடங்கி முதல் உடன் முடிவடைகிறது. maxHeapify இன் ஒவ்வொரு அழைப்பிற்கும், பெற்றோர் முனையின் இடது குழந்தை மற்றும் வலது குழந்தை, i, கண்டுபிடிக்கப்பட்டு, மூன்றில் எது பெரியது என்பதைக் கண்டறிய சோதனைகள் செய்யப்பட்டு, அதை maxVal என வரையறுக்கிறது . maxVal பெற்றோர் முனைக்கு சமமாக இல்லாவிட்டால் , பெற்றோர் முனை மற்றும் maxVal ஆகியவை மாற்றப்பட்டு, maxHeapify மீண்டும் இந்த முறை maxVal இல் அழைக்கப்படுகிறது மற்றும் முன்பு போலவே அதே படிகள் மேற்கொள்ளப்படும். இறுதியில் அதிகபட்சக் குவியல் உருவாக்கப்படும், மேலும் மேற்கொள்ள வேண்டிய மறு செய்கைகள் எதுவும் இருக்காது. புதுப்பிக்கப்பட்ட அணிவரிசை, வரிசை , இப்போது புதியஅரே என பிரதானத்திற்குத் திரும்பியது , பின்னர் ஒவ்வொரு தொடர்ச்சியான உறுப்புகளும் கன்சோலில் அச்சிடப்படும். புதிய வரிசைஇப்போது அதிகபட்சமாக உள்ளது. PriorityQueue ஐப் பயன்படுத்தி முந்தைய எடுத்துக்காட்டில் எண்கள் எழுதப்பட்டுள்ளன என்பதை நினைவில் கொள்ளவும்: ரூட், ரூட்டின் வலது-குழந்தை பெற்றோராக, ரூட்டின் இடது-குழந்தை பெற்றோராக, முதல் வலது-குழந்தையின் வலது-குழந்தை பெற்றோராக, இடது-முதல் குழந்தை பெற்றோராக இடது-குழந்தை, பெற்றோராக முதல் இடது-குழந்தையின் வலது-குழந்தை, பெற்றோராக முதல் வலது-குழந்தையின் இடது-குழந்தை, முதலியன. முன்னுரிமை வரிசையைப் பயன்படுத்தும் போது அவை சற்று வித்தியாசமான வரிசையில் உள்ளன, ஏனெனில் தொடர்ச்சியான கூறுகளுக்கு இடையே ஒப்பீடு செய்யப்படுகிறது . maxheapify எடுத்துக்காட்டில், கணு அணிவரிசையில் உள்ள அடுத்த இரண்டு தொடர்ச்சியான உறுப்புகளுடன் ஒப்பிடப்பட்டு மிகப்பெரிய மதிப்பிற்கு மாற்றப்பட்டது. சுருக்கமாக, இரண்டு வெவ்வேறு அல்காரிதம்கள் பயன்படுத்தப்படுகின்றன. இரண்டும் ஒரு அதிகபட்ச குவியலை உருவாக்குகின்றன.

முடிவுரை

எனவே இங்கே நாம் max heap மற்றும் அதை எப்படி PriorityQueue அல்லது Max Heapify அல்காரிதம் மூலம் உருவாக்கலாம் என்பதைப் பார்த்தோம் . ReverseOrder() உடன் PriorityQueue ஐப் பயன்படுத்துவது இதைச் செய்வதற்கான ஒரு நேர்த்தியான வழி மற்றும் பரிந்துரைக்கப்பட்ட முறை. இருப்பினும், ஜாவா ஜூனியருக்கான உங்கள் நேர்காணலில் வெற்றிபெற இது ஒரு நல்ல குறியீட்டு பயிற்சியாக இருக்கும் என்பதால், நீங்கள் இந்த எடுத்துக்காட்டுகளைப் படித்து உங்கள் சொந்த முறைகளை எழுதலாம்.