Java의 최대 힙

이진 트리

Java에는 다양한 유형의 데이터 구조가 있습니다. 힙은 이진 트리 라는 트리 구조를 기반으로 합니다 . 이진 트리는 노드로 구성되며 각 노드는 최대 2개의 자식 노드를 가질 수 있습니다.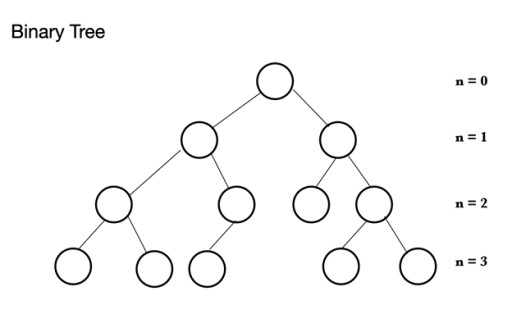 이진 트리는 0~2개의 노드를 가질 수 있는 부모 노드로 구성됩니다. 왼쪽 자식 노드 및/또는 오른쪽 자식 노드가 있거나 노드가 전혀 없을 수 있습니다. 완전한 이진 트리에서는 가득 찰 수 있지만 가득 찰 필요는 없는 마지막 수준을 제외하고 모든 노드가 채워집니다. 마지막 수준인 n번째 수준은 1~2n개의 노드를 가질 수 있습니다. 여기서 첫 번째는 n = 0에 있고 루트입니다.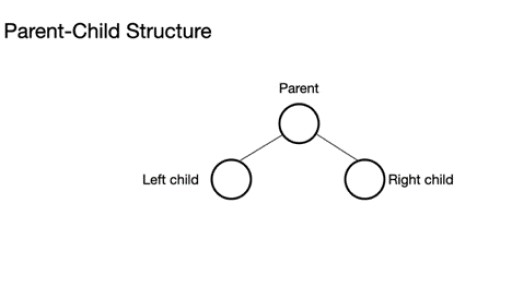

최대 힙

최대 힙(또는 maxheap)은 완전한 이진 트리 입니다 . 중요한 점은 부모 노드가 왼쪽 및 오른쪽 자식 노드보다 크거나 같은 값을 가져야 한다는 것입니다. 이를 준수하지 않으면 최대 힙이 없습니다. 반면에 최소 힙은 루트가 가장 작은 값이고 연속 노드의 값이 증가하는 반대입니다. 각 자식 노드는 부모보다 크거나 같은 값을 가집니다. 또한 완전한 이진 트리입니다. 최대 힙의 예는 다음과 같습니다.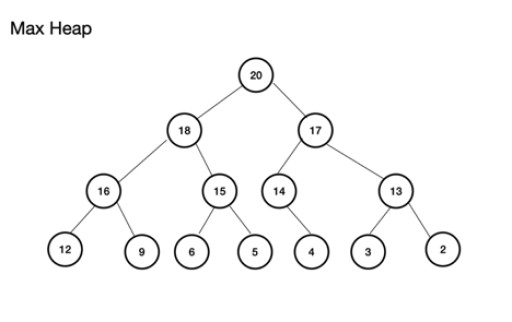 최대 힙은 배열에서 만들 수 있습니다. 이 배열은 트리 측면에서 생각됩니다. 힙의 경우 루트(트리의 최상위 부모 노드)가 위치(인덱스) n에 저장되면 배열 theArray 에 대해 theArray[n] 으로 정의됩니다.. 따라서 왼쪽 및 오른쪽 자식 노드는 각각 theArray[2n+1] 및 theArray[2n+2] 에 있습니다 . 최대 힙의 경우 루트는 theArray[0] 에 있습니다 . 레벨 n의 경우 루트 n = 0: theArr[n]은 부모 노드 theArr[(2*n)+1]은 왼쪽 자식 노드 theArr[(2*n)+2]는 오른쪽 자식 노드

PriorityQueue 클래스

Java의 힙은 PriorityQueue 클래스를 사용하여 구현할 수 있습니다 . PriorityQueues는 컬렉션에서 가장 중요하거나 가장 중요하지 않은 항목을 찾는 데 사용됩니다. PriorityQueue 클래스는 java.util.package 에서 찾을 수 있습니다 . PriorityQueue는 대기열에서 특정 순서로 배치되도록 비교할 수 있는 개체로 구성되어야 합니다. PriorityQueue는 비교자를 가질 수 있으므로 개체 간의 비교가 이루어지고 이 비교에 따라 대기열이 형성됩니다. 예를 들면 다음과 같습니다.

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

출력 제공: 이 예에서 intQueue 의 기본 크기 는 11이므로 명시되지 않았으며(일반적으로 비교기 앞의 첫 번째 인수) 비교기는 다음과 같이 지정되었습니다. 이것은 intQueue 의 항목을 비교하고 오름차순 배열 길이로 정렬합니다.

최대 힙 생성을 위한 PriorityQueue 구현

PriorityQueue 클래스 는 기본적으로 비교기가 없는 최소 힙입니다. 최소 힙은 최대 힙의 반대이므로 루트는 가장 작은 값이고 연속적인 자식 노드는 루트 및 후속 부모 노드보다 크거나 같습니다. 이러한 이유로 max heap의 경우 비교기로 Java의 Collections 프레임워크에서 reverseOrder()를 사용해야 합니다 . 이렇게 하면 최소 힙이 아닌 최대 힙을 얻을 수 있습니다. 이 클래스에는 add() , contains() , remove() , poll() 및 peek() 와 같은 유용한 메서드가 있습니다 . 요소는 대기열에 추가되며 어떤 순서로든 가능합니다. 새로운 PriorityQueue 대기열은 이러한 요소를 역순으로 최대 힙으로 저장합니다. 대기열이 작성되면 순서는 다음과 같습니다. 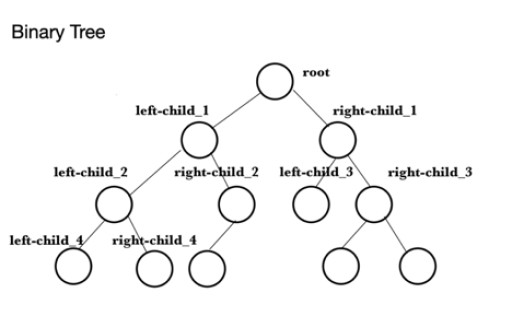루트 루트가 부모인 왼쪽 자식(Left-child_1) 루트가 부모인 오른쪽 자식(오른쪽-자식_1) 왼쪽 자식_1이 부모인 왼쪽 자식(왼쪽-자식_2) ) Right-child_1이 부모인 오른쪽 자식(Right-child_2) Right-child_1이 부모인 왼쪽 자식(Left-child_3) Right-child_1이 부모인 오른쪽 자식(Right-child_3) Left-child_2가 있는 왼쪽 자식 부모로(Left-child_4) Right-child, Left-child_2를 부모로(Right-child_4) 등다음 코드는 java에서 최대 힙(maxheap)을 생성하는 방법의 예입니다. 가장 먼저 할 일은 최대 힙이 생성될 값으로 배열을 채우는 것입니다. 이것을 theArray 라고 합니다 . 다음으로 PriorityQueue , theQueue 가 생성되고 theArray 의 요소가 여기에 추가됩니다. 이것은 add() 메소드를 사용합니다 . 예를 들어 theQueue.add(10)는 대기열 끝에 10을 추가합니다. PriorityQueue 클래스 의 일부 기능을 설명하기 위해 peek() 메서드를 사용하여 힙의 헤드를 찾습니다. 이 경우 최대값은 99입니다. 다음 작업은 힙의 크기를 확인하는 것입니다. 크기() 사용9로 확인되고 콘솔에 출력됩니다. writeMaxHeap 메서드는 루트, 루트가 부모인 왼쪽 자식, 루트가 부모인 오른쪽 자식, 첫 번째 왼쪽 자식이 부모인 왼쪽 자식, 첫 번째 왼쪽 자식이 있는 오른쪽 자식 순서로 큐의 요소를 씁니다. parent, 첫 번째 오른쪽 자식을 부모로 하는 right-child, 첫 번째 오른쪽 자식을 부모로 하는 left-child 등 위와 동일한 순서로 왼쪽 및 오른쪽 자식을 부모로 사용하는 후속 값. PriorityQueue 메서드 contains(J) 는 특정 요소 J 가 대기열에 있는지 확인하는 데 사용됩니다. 이 경우 J = 10을 찾습니다. 이 예에서 이것이 대기열에 있는 것이 참이므로 콘솔에 참으로 기록됩니다. 그런 다음 다른 PriorityQueue 메서드인 remove(J)를 사용하여 theQueue 에서 J = 10을 제거합니다 . PriorityQueue 의 더 많은 기능을 설명하기 위해 poll() 메서드를 사용하여 while 루프 를 사용하여 헤드 요소(최대값)를 제거하고 매번 새 대기열에서 헤드 요소를 제거하고 대기열 크기를 하나씩 줄입니다. 이것은 writeQueue 메서드에서 발생합니다.메인에서 호출합니다. 제거된 요소가 콘솔에 출력될 때마다. 원래 대기열에는 결국 요소가 남아 있지 않습니다. 인쇄된 요소는 값이 내림차순인 최대 힙이며 큐의 헤드가 매번 인쇄됩니다.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

산출:

맥스 히피파이

Max Heapify 알고리즘은 이진 트리가 최대 힙인지 확인하는 데 사용됩니다. 우리가 노드 n에 있고 그 자식 노드, 왼쪽 및 오른쪽도 최대 힙 자체인 경우 최대 힙이 있습니다. 트리 전체에서 그렇지 않은 경우 최대 힙이 없습니다. Max Heapify 알고리즘은 maxheap 원칙을 준수하도록 트리를 정렬하는 데 사용됩니다. Max Heapify는 하나의 노드에서만 작동합니다. 요구 사항이 배열이 최대 힙 배열인 경우 모든 하위 트리는 한 번에 하나씩 루트 전에 maxheap으로 변환되어야 합니다. 알고리즘은 각 노드에서 사용해야 합니다. 이것은 N/2 노드에서 수행됩니다(잎은 최대 힙 요구 사항을 준수함). 힙의 시간 복잡도는 O(NlogN)이고 높이 X에 있는 한 노드의 시간 복잡도는 O(X)입니다. 다음 코드는 트리(배열)를 최대화하는 방법을 보여줍니다.

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

출력 제공: 이 코드에서 theArray 가 생성되고 숫자로 채워집니다. 두 번째 배열 newArray 가 생성되고 이번에는 최대 힙 배열인 maxheapCreate 메서드의 결과가 포함됩니다. maxHeapCreate 메서드는 main 에서 호출되며 여기서 새 배열인 theNewArr 가 생성되고 maxHeapify 결과로 채워집니다. 이는 입력 배열 크기의 절반 이상을 반복하여 수행됩니다. 루프의 각 패스에 대해 maxHeapify 메서드 가 호출되어 배열 중간에 있는 요소에서 시작하여 첫 번째 요소로 끝납니다. maxHeapify 의 각 호출에 대해, 부모 노드 i의 왼쪽 자식과 오른쪽 자식을 찾고 세 개 중 가장 큰 것을 찾기 위해 검사를 수행하고 이를 maxVal 로 정의합니다 . maxVal이 부모 노드와 같지 않으면 교체가 수행되어 부모 노드와 maxVal 이 교체된 다음 이번에는 maxVal 에서 maxHeapify가 다시 호출되고 이전과 동일한 단계가 수행됩니다. 결국 최대 힙이 생성되고 더 이상 수행할 반복이 없습니다. 업데이트된 배열 array 는 이제 main에 newArray로 반환된 다음 각 연속 요소가 콘솔에 출력됩니다. newArray이제 최대 힙입니다. PriorityQueue를 사용하는 이전 예에서와 같이 숫자가 기록됩니다. 왼쪽 자식을 부모로, 첫 번째 왼쪽 자식의 오른쪽 자식을 부모로, 첫 번째 오른쪽 자식의 왼쪽 자식을 부모로 하는 등. 연속 요소 간에 비교가 이루어지기 때문에 PriorityQueue를 사용할 때와 순서가 약간 다릅니다. 반면 maxheapify 예에서는 노드가 배열의 다음 두 연속 요소와 비교되고 가장 큰 값으로 교환됩니다. 즉, 두 가지 다른 알고리즘이 사용됩니다. 둘 다 최대 힙을 생성합니다.

결론

그래서 여기에서 우리는 최대 힙과 PriorityQueue 또는 Max Heapify 알고리즘을 사용하여 생성할 수 있는 방법을 살펴보았습니다 . reverseOrder() 와 함께 PriorityQueue를 사용하는 것이 이를 수행하는 깔끔한 방법이며 권장되는 방법입니다. 그러나 Java Junior 인터뷰에서 성공하는 데 도움이 되는 좋은 코딩 연습이 될 것이기 때문에 이러한 예제를 연구하고 자신만의 방법을 작성할 수 있습니다.