Max Heap ใน Java

ต้นไม้ไบนารี

ใน Java มีโครงสร้างข้อมูลหลายประเภท ฮีปขึ้นอยู่กับโครงสร้างต้นไม้ที่เรียกว่าไบนารีทรี ไบนารีทรีประกอบด้วยโหนด ซึ่งแต่ละโหนดสามารถมีโหนดย่อยได้สูงสุด 2 โหนด: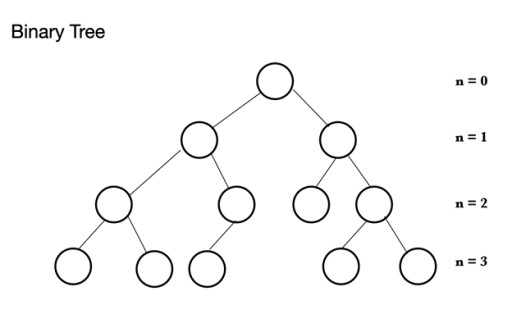 ไบนารีทรีประกอบด้วยโหนดพาเรนต์ซึ่งสามารถมีได้ตั้งแต่ 0 ถึง 2 โหนด สามารถมีโหนดลูกซ้ายและ/หรือโหนดลูกขวา หรือไม่มีโหนดเลยก็ได้ ในไบนารีทรีที่สมบูรณ์ โหนดทั้งหมดจะถูกเติม ยกเว้นระดับสุดท้ายที่สามารถเต็มได้ แต่ไม่จำเป็นต้องเต็ม ระดับสุดท้ายคือระดับที่ n สามารถมีโหนดได้ตั้งแต่ 1 ถึง 2n โดยที่โหนดแรกอยู่ที่ n = 0 และเป็นรูท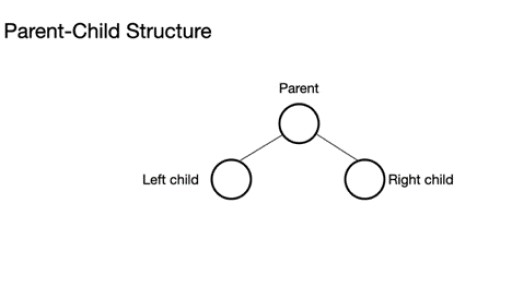

กองสูงสุด

Max heap (หรือ maxheap) เป็นไบนารีทรีที่สมบูรณ์ สิ่งสำคัญเกี่ยวกับมันคือโหนดหลักต้องมีค่ามากกว่าหรือเท่ากับโหนดซ้ายและขวาของโหนดย่อย หากไม่ปฏิบัติตาม คุณจะไม่มีฮีปสูงสุด ในทางกลับกัน Min heap นั้นตรงกันข้ามกับ root เป็นค่าที่เล็กที่สุดโดยโหนดที่ต่อเนื่องกันจะเพิ่มมูลค่า แต่ละโหนดลูกมีค่ามากกว่าหรือเท่ากับพาเรนต์ นอกจากนี้ยังเป็นต้นไม้ไบนารีที่สมบูรณ์ ตัวอย่างของฮีปสูงสุดคือ: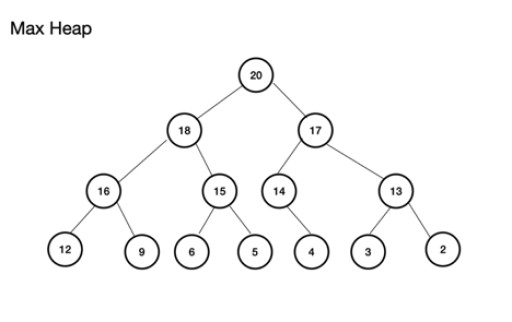 ฮีปสูงสุดสามารถสร้างได้จากอาร์เรย์ อาร์เรย์นี้จะคิดในแง่ของต้นไม้ สำหรับฮีป ถ้ารูท (โหนดพาเรนต์บนสุดของทรี) ถูกเก็บไว้ที่ตำแหน่ง (ดัชนี) n มันถูกกำหนดไว้สำหรับอาร์เรย์theArrayเป็นtheArray[n]. โหนดลูกซ้ายและขวาจึงอยู่ที่theArray[2n+1]และtheArray[2n+2]ตามลำดับ สำหรับฮีปสูงสุด รูทจะอยู่ที่theArray[0 ] สำหรับระดับ n รูท n = 0: theArr[n] เป็นโหนดแม่ theArr[(2*n)+1] เป็นโหนดลูกด้านซ้าย theArr[(2*n)+2] เป็นโหนดลูกด้านขวา

ระดับ PriorityQueue

ฮีปใน Java สามารถนำไปใช้ได้โดยใช้คลาสPriorityQueue PriorityQueuesใช้เพื่อค้นหารายการที่สำคัญที่สุดหรือน้อยที่สุดในคอลเลกชันคลาสPriorityQueueสามารถพบได้ในjava.util.package PriorityQueuesต้องประกอบด้วยอ็อบเจกต์ที่เทียบเคียงได้ เพื่อให้วางตามลำดับเฉพาะในคิว PriorityQueueสามารถมีตัวเปรียบเทียบเพื่อให้มีการเปรียบเทียบระหว่างวัตถุและคิวที่เกิดขึ้นตามการเปรียบเทียบนี้ ตัวอย่างคือ:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

ให้เอาต์พุต: ในตัวอย่างนี้ ขนาดเริ่มต้นของintQueueคือ 11 ดังนั้นจึงไม่มีการระบุ (โดยปกติจะเป็นอาร์กิวเมนต์แรกก่อนตัวเปรียบเทียบ) และได้รับตัวเปรียบเทียบเป็น: สิ่งนี้จะทำการเปรียบเทียบระหว่างรายการในintQueueและจัดเรียงเป็นความยาวของอาร์เรย์จากน้อยไปหามาก

การใช้ PriorityQueue เพื่อสร้าง Max Heap

PriorityQueue Class เริ่มต้นเป็น min heap โดยไม่มีตัวเปรียบเทียบ Min heap ตรงข้ามกับ max heap ดังนั้น root จึงเป็นค่าที่น้อยที่สุด และโหนดย่อยที่ตามมาจะมีขนาดใหญ่กว่าหรือเท่ากับ root และโหนดพาเรนต์ที่ตามมา ด้วยเหตุนี้ สำหรับ max heap จึงจำเป็นต้องใช้reverseOrder()จากเฟรมเวิร์ก Collections ของ Java เป็นตัวเปรียบเทียบ สิ่งนี้จะทำให้แน่ใจว่าเราได้รับฮีปสูงสุดไม่ใช่ฮีปขั้นต่ำ คลาสนี้มีเมธอดที่มีประโยชน์ เช่นadd() , container() , remove ( ) , poll()และpeek() องค์ประกอบจะถูกเพิ่มลงในคิวและสามารถอยู่ในลำดับใดก็ได้ คิว PriorityQueue ใหม่จะจัดเก็บองค์ประกอบเหล่านั้นเป็นกองสูงสุดในลำดับย้อนกลับ เมื่อคิวถูกเขียนออกมา ลำดับจะเป็น: Root Left-child with root (Left-child_1) Right-child with root as parent (Right-child_1) Left-child with Left-child_1 as parent (Left-child_2 ) เด็กขวากับเด็กซ้าย_1 เป็นผู้ปกครอง (ขวา-child_2) เด็กซ้ายกับเด็กขวา_1 เป็นผู้ปกครอง (ซ้าย-เด็ก_3) เด็กขวากับเด็กขวา_1 เป็นผู้ปกครอง (ขวา-เด็ก_3) เด็กซ้ายกับเด็กซ้าย_2 เป็น parent (Left-child_4) Right-child กับ Left-child_2 เป็น parent (Right-child_4) ฯลฯ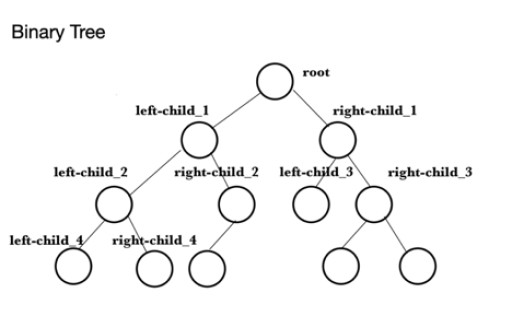โค้ดต่อไปนี้เป็นตัวอย่างของการสร้าง max heap (maxheap) ใน java สิ่งแรกที่ต้องทำคือเติมอาร์เรย์ด้วยค่าที่จะสร้างฮีปสูงสุด สิ่งนี้เรียกว่าtheArray ถัดไปPriorityQueue , theQueue จะถูกสร้างขึ้น จากนั้นจึง เพิ่มองค์ประกอบจากtheArray ลงในสิ่งนี้ สิ่งนี้ใช้วิธีการadd()เช่นtheQueue.add(10)เพื่อเพิ่ม 10 ต่อท้ายคิว เพื่อแสดงฟังก์ชันบางอย่างของ คลาส PriorityQueueจากนั้นเมธอด peek( ) จะ ถูกใช้เพื่อค้นหาส่วนหัวของฮีป และนี่คือค่าสูงสุด ในกรณีนี้คือ 99 งานต่อไปคือการตรวจสอบขนาดของฮีป ใช้ขนาด ()ซึ่งพบว่าเป็น 9 และพิมพ์ออกมาที่คอนโซล เมธอดwriteMaxHeapเขียนองค์ประกอบในคิวตามลำดับรูท, ลูกซ้ายที่มีรูทเป็นพาเรนต์, ลูกขวาที่มีรูทเป็นพาเรนต์, ลูกซ้ายที่มีลูกซ้ายคนแรกเป็นพาเรนต์, ลูกขวาที่มีลูกซ้ายตัวแรกเป็น parent, right-child กับ first right-child เป็น parent, left-child กับ first right-child เป็น parent ฯลฯ พร้อมค่าที่ตามมาโดยใช้ child ซ้ายและขวาเป็น parent ในลำดับเดียวกันกับด้านบน วิธีการPriorityQueue ประกอบด้วย (J)ใช้เพื่อค้นหาว่าองค์ประกอบเฉพาะ J อยู่ในคิวหรือไม่ ในกรณีนี้ เรามองหา J = 10 ในตัวอย่างของเรา เป็นจริงที่อยู่ในคิว ดังนั้นสิ่งนี้จึงเขียนไปยังคอนโซลว่าเป็นจริง วิธีPriorityQueue อีกวิธี หนึ่ง คือลบ ( J)เพื่อลบ J = 10 ออกจากtheQueue เพื่อแสดงฟังก์ชันการทำงานของPriorityQueue เพิ่มเติม เมธอดpoll()ใช้เพื่อลบองค์ประกอบส่วนหัว (ค่าสูงสุด) โดยใช้ การวนรอบ ขณะทุกครั้งที่ลบองค์ประกอบส่วนหัวในคิวใหม่ และลดขนาดคิวลงทีละรายการในแต่ละครั้ง สิ่งนี้เกิดขึ้นในเมธอดwriteQueueเรียกจากหลัก แต่ละครั้งที่องค์ประกอบที่ลบออกจะถูกพิมพ์ไปที่คอนโซล ในที่สุดคิวเดิมจะไม่มีองค์ประกอบเหลืออยู่ องค์ประกอบที่พิมพ์คือฮีปสูงสุดในลำดับค่ามากไปหาน้อย โดยที่ส่วนหัวของคิวจะถูกพิมพ์ออกมาในแต่ละครั้ง

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

เอาท์พุต:

Max Heapify

อัลกอริทึม Max Heapify ใช้เพื่อให้แน่ใจว่าไบนารีทรีเป็นฮีปสูงสุด ถ้าเราอยู่ที่โหนด n และโหนดลูกของมัน ทางซ้ายและขวาก็มีฮีปสูงสุดเช่นกัน ดีมาก เรามีฮีปสูงสุด หากไม่เป็นเช่นนั้นทั่วทั้งทรี แสดงว่าเราไม่มีฮีปสูงสุด อัลกอริทึม Max Heapify ใช้เพื่อจัดเรียงทรีเพื่อให้เป็นไปตามหลักการของ maxheap Max Heapify ทำงานบนโหนดเดียวเท่านั้น หากข้อกำหนดคือให้อาร์เรย์เป็นอาร์เรย์ฮีปสูงสุด ต้นไม้ย่อยทั้งหมดจะต้องถูกแปลงเป็นสูงสุดก่อนรูท ทีละรายการ ต้องใช้อัลกอริทึมในแต่ละโหนด สิ่งนี้จะทำบนโหนด N/2 (ลีฟจะเป็นไปตามข้อกำหนดฮีปสูงสุด) ความซับซ้อนของเวลาของฮีปคือ O(NlogN) และสำหรับหนึ่งโหนดที่ความสูง X ความซับซ้อนของเวลาคือ O(X) รหัสต่อไปนี้แสดงวิธีการขยายต้นไม้ (อาร์เรย์) ให้สูงสุด

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

ให้เอาต์พุต: ในโค้ดนี้Arrayจะถูกสร้างขึ้นและเติมด้วยตัวเลข อาร์เรย์ที่สองnewArrayถูกสร้างขึ้น และคราวนี้จะมีผลลัพธ์ของเมธอดmaxheapCreateอาร์เรย์ฮีปสูงสุด เมธอดmaxHeapCreateถูกเรียกจากmainและนี่คืออาร์เรย์ใหม่theNewArrที่ถูกสร้างขึ้นและเติมด้วยผลลัพธ์maxHeapify สิ่งนี้ทำได้โดยการวนซ้ำขนาดมากกว่าครึ่งหนึ่งของอาร์เรย์อินพุต สำหรับการวนซ้ำแต่ละครั้ง เมธอดmaxHeapifyเรียกว่าเริ่มต้นที่องค์ประกอบที่อยู่ตรงกลางของอาร์เรย์และสิ้นสุดด้วยองค์ประกอบแรก สำหรับการโทรmaxHeapify แต่ละครั้ง, ลูกซ้ายและลูกขวาของโหนดพาเรนต์, i ถูกพบและทำการตรวจสอบเพื่อค้นหาว่า อันไหนใหญ่ที่สุดในสามโหนดโดยกำหนดว่าเป็นmaxVal หากmaxValไม่เท่ากับโหนดพาเรนต์ การสลับจะเสร็จสิ้นเพื่อให้โหนดพาเรนต์และmaxValถูกสลับ จากนั้น จึงเรียก maxHeapifyอีกครั้งในmaxValและดำเนินการตามขั้นตอนเดิมเหมือนก่อนหน้านี้ ในที่สุดฮีปสูงสุดจะถูกสร้างขึ้น และจะไม่มีการทำซ้ำอีกต่อไป อาร์เรย์ที่อัปเดตแล้วarrayจะถูกส่งกลับไปยังmainเป็นnewArrayจากนั้นแต่ละองค์ประกอบที่ต่อเนื่องกันจะพิมพ์ออกมาที่คอนโซล ใหม่อาร์เรย์ตอนนี้เป็นกองสูงสุด โปรดทราบว่าในตัวอย่างก่อนหน้านี้โดยใช้ PriorityQueueตัวเลขจะถูกเขียนออกมา: root, right-child of root as parent, left-child of root as parent, right-child of first right-child of first, right-child of first. ลูกซ้ายเป็นพาเรนต์, ลูกขวาของลูกซ้ายคนแรกเป็นพาเรนต์, ลูกซ้ายของลูกขวาคนแรกเป็นพาเรนต์ ฯลฯ พวกเขาอยู่ในลำดับที่แตกต่างกันเล็กน้อยเมื่อใช้ PriorityQueue เนื่องจากการเปรียบเทียบจะทำระหว่างองค์ประกอบที่ต่อเนื่องกัน ในขณะที่ตัวอย่าง maxheapify โหนดจะถูกเปรียบเทียบกับสององค์ประกอบที่ต่อเนื่องกันถัดไปในอาร์เรย์และสลับเป็นค่าที่ใหญ่ที่สุด กล่าวโดยสรุปคือ ใช้อัลกอริทึมที่แตกต่างกันสองแบบ ทั้งสองสร้างกองสูงสุด

บทสรุป

ดังนั้นเราจึงดูที่ max heap และวิธีการสร้างด้วย PriorityQueueหรือ Max Heapify อัลกอริทึม การใช้PriorityQueueกับreverseOrder()เป็นวิธีที่เรียบร้อยและเป็นวิธีที่แนะนำ อย่างไรก็ตาม คุณสามารถศึกษาตัวอย่างเหล่านี้และเขียนวิธีการของคุณเองได้ เนื่องจากนี่จะเป็นแบบฝึกหัดการเขียนโค้ดที่ดีที่จะช่วยให้คุณประสบความสำเร็จในการสัมภาษณ์สำหรับ Java Junior