Maksymalna sterta w Javie

Drzewo binarne

W Javie istnieje wiele różnych typów struktur danych. Sterta jest oparta na strukturze drzewa zwanej drzewem binarnym . Drzewo binarne składa się z węzłów, z których każdy może mieć maksymalnie 2 węzły podrzędne: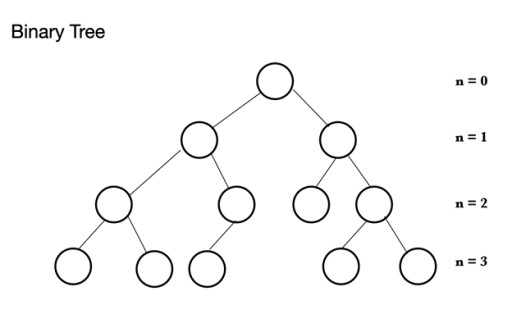 Drzewo binarne składa się z węzła nadrzędnego, który może mieć od 0 do 2 węzłów. Może mieć lewy węzeł podrzędny i/lub prawy węzeł podrzędny lub w ogóle nie mieć węzłów. W pełnym drzewie binarnym wszystkie węzły są wypełnione, z wyjątkiem ostatniego poziomu, który może być pełny, ale nie musi być pełny. Ostatni poziom, n-ty poziom, może mieć od 1 do 2n węzłów, gdzie pierwszy znajduje się w n = 0 i jest pierwiastkiem.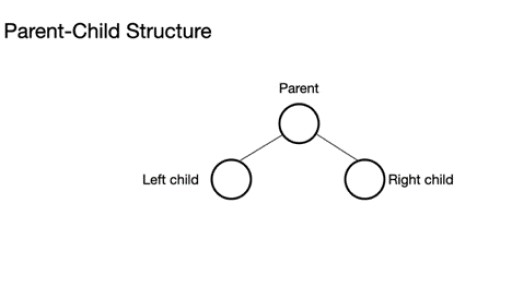

Maks. sterta

Maks. sterta (lub maks. sterta) to kompletne drzewo binarne . Ważną rzeczą jest to, że węzeł nadrzędny MUSI mieć wartość większą lub równą wartości lewego i prawego węzła podrzędnego. Jeśli nie jest to przestrzegane, nie masz maksymalnej sterty. Min sterta, z drugiej strony, jest odwrotna z pierwiastkiem jako najmniejszą wartością, a kolejne węzły zyskują na wartości; każdy węzeł podrzędny ma wartość większą lub równą swojemu rodzicowi. Jest to również kompletne drzewo binarne. Przykładem maksymalnej sterty jest: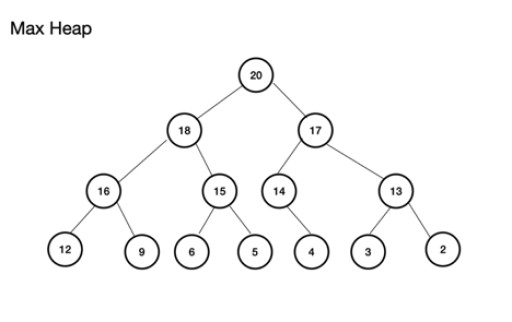 Maksymalna sterta może być zbudowana z tablicy. Ta tablica będzie traktowana w kategoriach drzewa. W przypadku sterty, jeśli korzeń (najwyższy węzeł nadrzędny drzewa) jest przechowywany w pozycji (indeksie) n, jest on zdefiniowany dla tablicy, theArray , jako theArray[n]. Lewe i prawe węzły potomne znajdują się zatem odpowiednio w theArray[2n+1] i theArray[2n+2] . Dla maksymalnej sterty korzeń znajduje się w theArray[0] . Dla poziomu n, pierwiastek n = 0: theArr[n] jest węzłem nadrzędnym theArr[(2*n)+1] jest lewym węzłem podrzędnym theArr[(2*n)+2] jest prawym węzłem podrzędnym

Klasa PriorityQueue

Sterty w Javie można zaimplementować przy użyciu klasy PriorityQueue . Kolejki PriorityQueue służą do znalezienia najważniejszego lub najmniej ważnego elementu w kolekcji. Klasę PriorityQueue można znaleźć w pakiecie java.util.package . PriorityQueues muszą być utworzone z obiektów, które są porównywalne, tak aby były umieszczane w określonej kolejności w kolejce. PriorityQueue może mieć komparator, dzięki czemu dokonuje się porównania między obiektami i kolejki utworzonej zgodnie z tym porównaniem. Przykładem jest:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Podanie danych wyjściowych: W tym przykładzie domyślnym rozmiarem intQueue jest 11, więc nie podano (zwykle jest to pierwszy argument przed komparatorem), a komparator podano jako: Spowoduje to porównanie elementów w intQueue i posortowanie ich według długości tablicy w porządku rosnącym.

Implementacja PriorityQueue w celu utworzenia maksymalnej sterty

Domyślnie klasa PriorityQueue to min sterta bez komparatora. Sterta minimalna jest przeciwieństwem sterty maksymalnej, więc korzeń jest najmniejszą wartością, a kolejne węzły potomne są większe lub równe węzłom głównym i kolejnym węzłom nadrzędnym. Z tego powodu dla maksymalnej sterty konieczne jest użycie reverseOrder() z frameworka Java Collections jako komparatora. Zapewni to, że otrzymamy maksymalną stertę, a nie minimalną stertę. Ta klasa ma przydatne metody, takie jak add() , zawiera() , remove() , poll() i peek() . Elementy są dodawane do kolejki i mogą być w dowolnej kolejności. Nowa kolejka PriorityQueue będzie przechowywać te elementy jako maksymalną stertę w odwrotnej kolejności. Gdy kolejka zostanie wypisana, kolejność będzie następująca: Root Lewe dziecko z rootem jako rodzicem (Left-child_1) Prawe dziecko z rootem jako rodzicem (Right-child_1) Lewe dziecko z Left-child_1 jako rodzicem (Left-child_2 ) Prawe dziecko z lewym dzieckiem_1 jako rodzicem (Prawe dziecko_2) Lewe dziecko z prawym dzieckiem_1 jako rodzicem (Left-child_3) Prawe dziecko z prawym dzieckiem_1 jako rodzicem (Prawe dziecko_3) Lewe dziecko z lewym dzieckiem_2 jako rodzic (lewe dziecko_4) prawe dziecko z lewym dzieckiem_2 jako rodzicem (prawe dziecko_4) itd.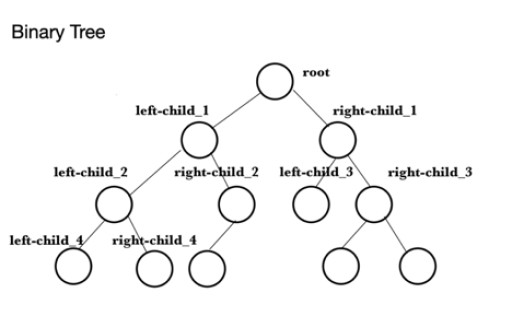Poniższy kod jest przykładem tworzenia maksymalnej sterty (maxheap) w Javie. Pierwszą rzeczą do zrobienia jest wypełnienie tablicy wartościami, dla których zostanie utworzona maksymalna sterta. Nazywa się to tablicą . Następnie tworzona jest PriorityQueue , theQueue , a następnie dodawane są do niej elementy z tablicy . Używa metody add() , np. theQueue.add(10) , aby dodać 10 na końcu kolejki. Aby zilustrować niektóre funkcje klasy PriorityQueue , metoda peek() jest następnie używana do znalezienia początku sterty i jest to maksymalna wartość, w tym przypadku 99. Kolejnym zadaniem jest sprawdzenie rozmiaru sterty używając rozmiaru ()która wynosi 9 i jest drukowana na konsoli. Metoda writeMaxHeap zapisuje elementy w kolejce w kolejności root, lewe dziecko z rootem jako rodzicem, prawe dziecko z rootem jako rodzicem, lewe dziecko z pierwszym lewym dzieckiem jako rodzicem, prawe dziecko z pierwszym lewym dzieckiem jako rodzicem rodzic, prawe dziecko z pierwszym prawym dzieckiem jako rodzicem, lewe dziecko z pierwszym prawym dzieckiem jako rodzicem itp., z kolejnymi wartościami używając lewego i prawego dziecka jako rodziców w takiej samej kolejności jak powyżej. Metoda PriorityQueue zawiera(J) służy do sprawdzania, czy określony element, J, znajduje się w kolejce . W tym przypadku szukamy J = 10. W naszym przykładzie prawdą jest, że to jest w kolejce, więc jest to zapisywane w konsoli jako prawda. Inna metoda PriorityQueue , remove(J) jest następnie używana do usunięcia J = 10 z theQueue . Aby lepiej zilustrować funkcjonalność PriorityQueue , użyto metody poll() do usunięcia elementu head (maksymalna wartość) za pomocą pętli while , za każdym razem usuwając element head w nowej kolejce i zmniejszając rozmiar kolejki za każdym razem o jeden. Dzieje się tak w metodzie writeQueuewywołany z głównego Za każdym razem usunięty element jest drukowany na konsoli. Oryginalna kolejka ostatecznie nie będzie miała żadnych elementów. Wydrukowane elementy to maksymalna sterta w kolejności malejącej wartości, gdzie za każdym razem drukowany jest początek kolejki.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Wyjście:

Max Heapify

Algorytm Max Heapify służy do zapewnienia, że ​​drzewo binarne jest stertą maksymalną. Jeśli jesteśmy w węźle n, a jego węzły potomne, lewy i prawy, również same są maksymalnymi stertami, to świetnie, mamy maksymalną stertę. Jeśli tak nie jest w całym drzewie, nie mamy maksymalnej sterty. Algorytm Max Heapify służy do sortowania drzewa tak, aby było zgodne z zasadami maxheap. Max Heapify działa tylko na jednym węźle. Jeśli wymaga się, aby tablica była tablicą o maksymalnej stercie, wszystkie drzewa podrzędne muszą zostać przekonwertowane na maksymalną stertę przed korzeniem, pojedynczo. Algorytm musi być używany w każdym węźle. Zostanie to zrobione na N/2 węzłach (liście będą zgodne z maksymalnymi wymaganiami sterty). Złożoność czasowa sterty wynosi O(NlogN), a dla jednego węzła na wysokości X złożoność czasowa wynosi O(X). Poniższy kod pokazuje, jak maksymalizować drzewo (tablicę).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Podanie danych wyjściowych: W tym kodzie tablica jest tworzona i wypełniana liczbami. Tworzona jest druga tablica, newArray , która tym razem będzie zawierała wynik działania metody maxheapCreate , tablicę sterty maksymalnej. Metoda maxHeapCreate jest wywoływana z main i tutaj tworzona jest nowa tablica, theNewArr i wypełniana wynikami maxHeapify . Odbywa się to poprzez zapętlenie ponad połowy rozmiaru tablicy wejściowej. Dla każdego przebiegu pętli wywoływana jest metoda maxHeapify , zaczynając od elementu w środku tablicy i kończąc na pierwszym. Dla każdego wywołania maxHeapify, zostaje znalezione lewe dziecko i prawe dziecko węzła nadrzędnego, i, i przeprowadzane są kontrole, aby znaleźć największy z trzech, definiując to jako maxVal . Jeśli maxVal nie jest równy węzłowi nadrzędnemu, następuje zamiana, tak że węzeł nadrzędny i maxVal są zamienione, a następnie maxHeapify jest ponownie wywoływany tym razem na maxVal i wykonywane są te same kroki, co poprzednio. W końcu utworzona zostanie maksymalna sterta i nie będzie już więcej iteracji do wykonania. Zaktualizowana tablica, array , jest teraz zwracana do main jako newArray , a następnie każdy kolejny element jest drukowany na konsoli. nowa tablicajest teraz maksymalną stertą. Zauważ, że podobnie jak w poprzednim przykładzie przy użyciu PriorityQueue liczby są zapisywane: korzeń, prawe dziecko korzenia jako rodzic, lewe dziecko korzenia jako rodzic, prawe dziecko pierwszego prawego dziecka jako rodzic, lewe dziecko pierwszego lewe dziecko jako rodzic, prawe dziecko pierwszego lewego dziecka jako rodzic, lewe dziecko pierwszego prawego dziecka jako rodzic itp. Są one w nieco innej kolejności niż w przypadku korzystania z PriorityQueue, ponieważ porównanie odbywa się między kolejnymi elementami podczas gdy w przykładzie maxheapify węzeł jest porównywany z dwoma kolejnymi elementami tablicy i zamieniany na największą wartość. Krótko mówiąc, stosowane są dwa różne algorytmy. Oba tworzą maksymalną stertę.

Wniosek

Więc tutaj przyjrzeliśmy się maksymalnemu stertowi i temu, jak można go utworzyć za pomocą algorytmu PriorityQueue lub Max Heapify. Używanie PriorityQueue z reverseOrder() to dobry sposób na zrobienie tego i zalecana metoda. Możesz jednak przestudiować te przykłady i napisać własne metody, ponieważ będzie to dobre ćwiczenie z kodowania, które pomoże ci odnieść sukces na rozmowie kwalifikacyjnej dla Java Junior.