Max Heap ing Jawa

Wit Binar

Ing Jawa, ana macem-macem jinis struktur data. Tumpukan kasebut adhedhasar struktur wit sing diarani wit biner . Wit binar kasusun saka simpul, sing saben bisa duwe maksimal 2 simpul anak: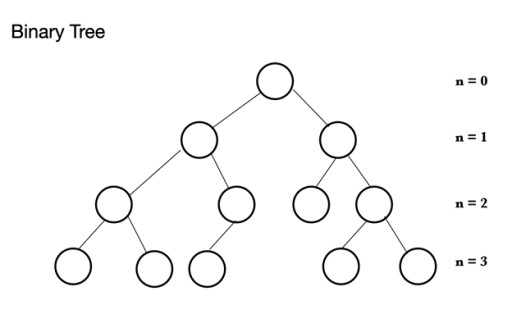 Wit binar kasusun saka simpul induk sing bisa duwe saka 0 nganti 2 simpul. Bisa duwe simpul anak kiwa lan / utawa simpul anak tengen, utawa ora ana simpul. Ing wit binar lengkap, kabeh simpul diisi kajaba tingkat pungkasan sing bisa kebak, nanging ora perlu kebak. Tingkat pungkasan, tingkat n, bisa duwe simpul 1 nganti 2n, ing endi sing pisanan ana ing n = 0 lan minangka oyod.

Tumpukan Max

Max heap (utawa maxheap) minangka wit binar lengkap . Sing penting yaiku simpul induk kudu duwe nilai sing luwih gedhe tinimbang utawa padha karo simpul anak kiwa lan tengen. Yen iki ora dipatuhi, sampeyan ora duwe tumpukan maksimal. Min tumpukan, ing tangan liyane, ngelawan karo ROOT minangka nilai paling cilik karo simpul sukses mundhak ing Nilai; saben simpul anak nduweni nilai sing luwih gedhe tinimbang utawa padha karo induke. Iku uga wit binar lengkap. Conto tumpukan maksimal yaiku: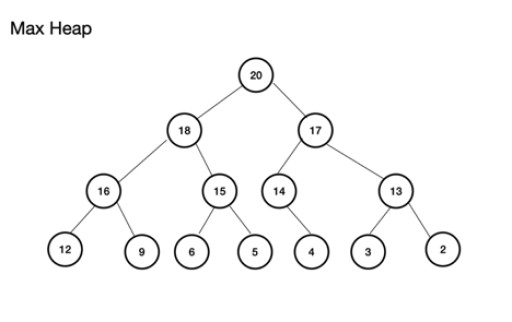 tumpukan maks bisa dibangun saka array. Array iki bakal dipikirake babagan wit. Kanggo tumpukan, yen root, (simpul induk ndhuwur wit) disimpen ing posisi (indeks) n, ditetepake kanggo array, theArray , minangka theArray[n]. Node anak kiwa lan tengen ana ing Array[2n+1] lan Array[2n+2] . Kanggo tumpukan maksimal, oyod ana ing Array[0] . Kanggo level n, root n = 0: theArr[n] minangka simpul induk theArr[(2*n)+1] yaiku simpul anak kiwa theArr[(2*n)+2] yaiku simpul anak tengen

Kelas PriorityQueue

Heaps ing Jawa bisa diimplementasikake nggunakake Kelas PriorityQueue . PriorityQueues digunakake kanggo nemokake item paling utawa paling penting ing koleksi.Kelas PriorityQueue bisa ditemokake ing java.util.package . PriorityQueues kudu kawangun saka obyek sing iso dibandhingke supaya padha diselehake ing urutan tartamtu ing antrian. PriorityQueue bisa duwe comparator supaya comparison antarane obyek digawe lan antrian kawangun miturut comparison iki. Tuladhane yaiku:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Menehi output: Ing conto iki, ukuran standar intQueue yaiku 11, mula durung dicritakake (biasane argumen pisanan sadurunge komparator) lan komparator diwenehi: Iki bakal nggawe mbandhingake antarane item ing intQueue lan ngurutake dadi dawa array saka urutan munggah.

Implementasine PriorityQueue kanggo Nggawe Heap Max

Kelas PriorityQueue standar kanggo tumpukan min tanpa komparator. Min heap minangka kebalikan saka max heap lan ROOT minangka nilai paling cilik lan simpul anak sing berturut-turut luwih gedhe utawa padha karo akar lan kelenjar parental sakteruse. Mulane, kanggo numpuk max, perlu nggunakake reverseOrder () saka framework Koleksi Jawa minangka komparator. Iki bakal njamin kita entuk tumpukan maksimal lan dudu tumpukan min. Kelas iki nduweni cara sing migunani kayata add() , ngemot() , mbusak() , poll() , lan peek() . Unsur ditambahake ing antrian lan bisa ing urutan apa wae. Antrian PriorityQueue anyar bakal nyimpen unsur kasebut minangka tumpukan maksimal kanthi urutan mbalikke. Nalika antrian ditulis, urutane bakal dadi: Root Kiwa-anak kanthi oyot minangka wong tuwa (Kiwa-anak_1) Anak-tengen kanthi oyot minangka wong tuwa (Tengen-anak_1) Kiwa-anak karo Kiri-anak_1 minangka wong tuwa (Kiwa-anak_2 ) Anak-tengen karo anak-kiwa_1 minangka wong tuwa (anak-tengen_2) Anak-kiwa karo anak-tengen_1 minangka wong tuwa (anak-kiwa_3) Anak-kiwa karo anak-tengen_1 minangka wong tuwa (anak-tengen_3) Anak-kiwa karo anak-kiwa_2 minangka wong tuwa (Kiri-anak_4) Kanan-anak karo Kiri-anak_2 minangka wong tuwa (Kiri-anak_4), lspKode ing ngisor iki minangka conto carane max heap (maxheap) digawe ing java. Babagan pisanan sing kudu ditindakake yaiku ngisi array kanthi nilai sing bakal digawe tumpukan maksimal. Iki diarani Array . Sabanjure, PriorityQueue , theQueue , digawe banjur unsur saka theArray ditambahake menyang iki. Iki nggunakake cara nambah () , contone, queue.add (10) kanggo nambah 10 kanggo mburi antrian. Kanggo ilustrasi sawetara fungsi saka PriorityQueue Class, metode Ndeleng () banjur digunakake kanggo nemokake sirah numpuk, lan iki nilai maksimum, ing kasus iki, 99. Tugas sabanjuré mriksa ukuran numpuk. nggunakake ukuran ()kang ketemu 9 lan iki dicithak metu kanggo console. Metode writeMaxHeap nulis unsur-unsur ing antrian kanthi urutan root, anak kiwa kanthi root minangka wong tuwa, anak tengen karo root minangka wong tuwa, anak kiwa karo anak kiwa pisanan minangka wong tuwa, anak tengen karo anak kiwa pisanan minangka tiyang sepah, anak tengen karo anak tengen pisanan minangka tiyang sepah, anak kiwa karo anak tengen pisanan minangka tiyang sepah etc, karo nilai sakteruse nggunakake anak kiwa lan tengen minangka tuwane ing urutan padha ing ndhuwur. Metode PriorityQueue ngemot (J) digunakake kanggo mangerteni apa unsur tartamtu, J, ana ing antrian . Ing kasus iki kita katon kanggo J = 10. Ing conto kita, iku bener sing iki ing antrian supaya iki ditulis metu kanggo console minangka bener. Cara PriorityQueue liyane , mbusak (J) banjur digunakake kanggo mbusak J = 10 saka queue . Kanggo ilustrasi liyane saka fungsi PriorityQueue , polling cara () digunakake kanggo mbusak unsur sirah (nilai maksimum) nggunakake daur ulang nalika , saben wektu njabut unsur sirah ing antrian anyar lan suda antrian ing ukuran saben wektu. Iki kedadeyan ing metode writeQueuedisebut saka utama. Saben unsur dibusak dicithak menyang console. Antrian asli pungkasane ora ana unsur sing isih ana. Unsur sing dicithak minangka tumpukan maksimal kanthi urutan nilai sing mudhun, ing ngendi kepala antrian dicithak saben wektu.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Output:

Max Heapify

Algoritma Max Heapify digunakake kanggo mesthekake yen wit binar minangka tumpukan maksimal. Yen kita ana ing simpul, n, lan kelenjar anak sawijining, kiwa lan tengen uga max heaps piyambak, banjur gedhe, kita duwe numpuk max. Yen iki ora kedadeyan ing saindenging wit, mula kita ora duwe tumpukan maksimal. Algoritma Max Heapify digunakake kanggo ngurutake wit supaya manut prinsip maxheap. Max Heapify mung dianggo ing siji simpul. Yen sarat yaiku array kasebut minangka array heap maksimal, mula kabeh sub wit kudu diowahi dadi maxheap sadurunge root, siji-sijine. Algoritma kudu digunakake ing saben simpul. Iki bakal ditindakake ing simpul N / 2 (godhong bakal netepi syarat tumpukan maksimal). Kompleksitas wektu tumpukan yaiku O(NlogN), lan kanggo siji simpul ing dhuwur X, kompleksitas wektu yaiku O(X). Kode ing ngisor iki nuduhake carane maxheapify wit (array).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Menehi output: Ing kode iki, Array digawe lan diisi karo nomer. Array kapindho, newArray , digawe lan wektu iki bakal ngemot asil metode, maxheapCreate , array tumpukan maksimal. Cara maxHeapCreate diarani saka main , lan ing kene array anyar, theNewArr , digawe lan diisi karo asil maxHeapify . Iki ditindakake kanthi ngubungake luwih saka setengah ukuran array input. Kanggo saben pass saka daur ulang, cara maxHeapify , diarani miwiti ing unsur ing tengah Uploaded lan pungkasan karo pisanan. Kanggo saben telpon saka maxHeapify, anak kiwa lan anak tengen simpul tiyang sepah, i, ketemu lan mriksa rampung kanggo nemokake kang paling gedhe saka telu, nemtokake sing minangka maxVal . Yen maxVal ora padha karo simpul induk banjur swap ditindakake supaya simpul induk lan maxVal diganti banjur maxHeapify diarani maneh ing maxVal lan langkah sing padha ditindakake kaya sadurunge. Pungkasane tumpukan maksimal bakal digawe lan ora ana maneh pengulangan sing kudu ditindakake. Array sing dianyari, array , saiki bali menyang utama minangka newArray banjur saben unsur berturut-turut dicithak menyang konsol. newArraysaiki dadi tumpukan maksimal. Elinga, kaya ing conto sadurunge nggunakake PriorityQueue nomer kasebut ditulis: ROOT, anak tengen ROOT minangka wong tuwa, anak kiwa saka ROOT minangka wong tuwa, anak tengen anak tengen pisanan minangka wong tuwa, anak kiwa saka pisanan. anak kiwa minangka wong tuwa, anak tengen anak kiwa pisanan minangka wong tuwa, anak kiwa anak tengen minangka wong tuwa, lan sapiturute. Urutane rada beda karo nalika nggunakake PriorityQueue amarga mbandhingake ditindakake ing antarane unsur sing berturut- turut . dene ing conto maxheapify, simpul dibandhingake karo loro unsur sukses sabanjuré ing Uploaded lan swapped kanggo Nilai paling gedhe. Ing cendhak, loro algoritma beda digunakake. Loro-lorone nggawe tumpukan maksimal.

Kesimpulan

Dadi ing kene kita wis ndeleng tumpukan max lan carane bisa digawe nganggo algoritma PriorityQueue utawa Max Heapify. Nggunakake PriorityQueue karo reverseOrder () iku cara apik kanggo nindakake iki lan cara dianjurake. Nanging, sampeyan bisa sinau conto iki lan nulis cara dhewe amarga iki bakal dadi latihan coding sing apik kanggo mbantu sampeyan sukses ing wawancara kanggo Java Junior.