Max Heap i Java

Det binære træ

I Java er der mange forskellige typer af datastrukturer. Hoben er baseret på en træstruktur kaldet et binært træ . Et binært træ består af noder, som hver maksimalt kan have 2 underordnede noder: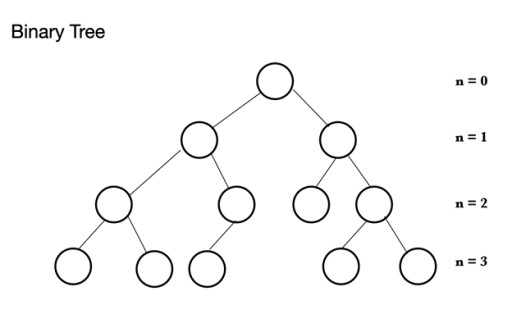 Et binært træ består af en overordnet node, som kan have fra 0 til 2 noder. Den kan have en venstre-under-knude og/eller en højre-under-knude, eller slet ingen knude. I et komplet binært træ er alle noder udfyldt undtagen det sidste niveau, som kan være fuldt, men ikke behøver at være fuldt. Det sidste niveau, det n'te niveau, kan have fra 1 til 2n noder, hvor det første er ved n = 0 og er roden.

Max Heap

Max heap (eller maxheap) er et komplet binært træ . Det vigtige ved det er, at den overordnede node SKAL have en værdi, der er større end eller lig med værdien for venstre og højre underordnede noder. Hvis dette ikke overholdes, har du ikke en max bunke. Min heap er på den anden side det modsatte med roden som den mindste værdi med successive noder stigende i værdi; hver underordnede node har en værdi, der er større end eller lig med dens overordnede. Det er også et komplet binært træ. Et eksempel på en max heap er: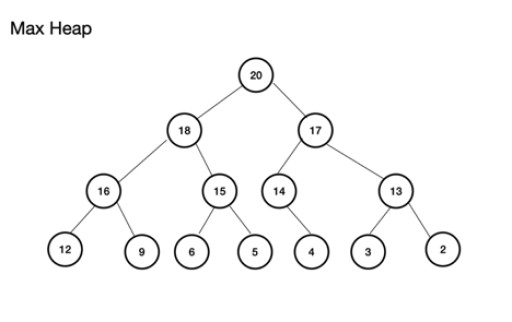 Max heap kan bygges ud fra et array. Dette array vil blive tænkt som et træ. For en heap, hvis roden (øverste overordnede node af træet) er lagret i position (indeks) n, er den defineret for array, theArray , som theArray[n]. Venstre og højre underordnede noder er derfor ved henholdsvis Array[2n+1] og Array[2n+2] . For den maksimale heap er roden ved theArray[0] . For niveau n er rod n = 0: Arr[n] er overordnet node Arr[(2*n)+1] er venstre underknude Arr[(2*n)+2] er højre underknude

Klassen PriorityQueue

Heaps i Java kan implementeres ved hjælp af PriorityQueue Class. PriorityQueue bruges til at finde det vigtigste eller mindst vigtige element i en samling. PriorityQueue- klassen kan findes i java.util.package . Prioritetskøer skal dannes af objekter, der er sammenlignelige, så de placeres i en bestemt rækkefølge i køen. PriorityQueue kan have en komparator, så der laves en sammenligning mellem objekterne og køen dannet i henhold til denne sammenligning. Et eksempel er:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Giver output: I dette eksempel er standardstørrelsen for intQueue 11, så den er ikke blevet angivet (normalt det første argument før komparatoren), og komparatoren er blevet givet som: Dette vil foretage en sammenligning mellem elementerne i intQueue og sortere dem i arraylængder i stigende rækkefølge.

Implementering af PriorityQueue for at skabe en Max Heap

PriorityQueue Class er standard til min heap uden en komparator . Min. heap er det modsatte af maks. heap, og så roden er den mindste værdi, og efterfølgende underordnede noder er større eller lig med roden og efterfølgende forældreknuder. Af denne grund, for max heap, er det nødvendigt at bruge reverseOrder() fra Javas Collections framework som komparator. Dette vil sikre, at vi får en max heap og ikke en min heap. Denne klasse har nyttige metoder såsom add() , contains() , remove() , poll() og peek() . Elementer føjes til køen og kan være i enhver rækkefølge. Den nye PriorityQueue-kø vil gemme disse elementer som en maksimal bunke i omvendt rækkefølge. Når køen er skrevet ud, vil rækkefølgen være: Rod Venstre-barn med rod som forælder (Venstre-barn_1) Højre-barn med rod som forælder (Højre-barn_1) Venstre-barn med Venstre-barn_1 som forælder (Venstre-barn_2) ) Højre-barn med Venstre-barn_1 som forælder (Højre-barn_2) Venstre-barn med Højre-barn_1 som forælder (Venstre-barn_3) Højre-barn med Højre-barn_1 som forælder (Højre-barn_3) Venstre-barn med Venstre-barn_2 som forælder (Venstre-barn_4) Højre-barn med Venstre-barn_2 som forælder (Højre-barn_4) osv.Følgende kode er et eksempel på, hvordan en max heap (maxheap) oprettes i java. Den første ting at gøre er at fylde et array med de værdier, som den maksimale heap vil blive oprettet for. Dette kaldes theArray . Dernæst oprettes en PriorityQueue , theQueue , og derefter tilføjes elementerne fra theArray til denne. Dette bruger metoden add() , f.eks. theQueue.add(10) for at tilføje 10 til slutningen af ​​køen. For at illustrere noget af funktionaliteten af ​​PriorityQueue Class, bruges metode peek() så til at finde hovedet af heapen, og dette er den maksimale værdi, i dette tilfælde, 99. Den næste opgave er at kontrollere størrelsen af ​​heapen. bruger størrelse()som viser sig at være 9 og denne printes ud til konsollen. Metode writeMaxHeap udskriver elementerne i køen i rækkefølge efter rod, venstre-barn med rod som forælder, højre-barn med rod som forælder, venstre-barn med første venstre-barn som forælder, højre-barn med første venstre-barn som forælder, højre-barn med første højre-barn som forælder, venstre-barn med første højre-barn som forælder osv., med efterfølgende værdier, der bruger venstre og højre barn som forældre i samme rækkefølge som ovenfor. PriorityQueue - metoden contains(J) bruges til at finde ud af, om et specifikt element, J, er i en kø. I dette tilfælde ser vi efter J = 10. I vores eksempel er det rigtigt, at dette er i køen, så dette skrives ud til konsollen som sandt. En anden PriorityQueue- metode, remove(J) bruges derefter til at fjerne J = 10 fra theQueue . For at illustrere mere af funktionaliteten af ​​PriorityQueue , bruges metode poll() til at fjerne head-elementet (maksimal værdi) ved hjælp af en while -løkke, hvor man hver gang fjerner head-elementet i den nye kø og mindsker køen i størrelse med én hver gang. Dette sker i metoden writeQueuekaldet fra main. Hver gang det fjernede element udskrives på konsollen. Den oprindelige kø vil til sidst ikke have nogen elementer tilbage. De udskrevne elementer er den maksimale heap i faldende værdi, hvor hovedet af køen udskrives hver gang.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Produktion:

Max Heapify

Max Heapify-algoritmen bruges til at sikre, at et binært træ er en max heap. Hvis vi er ved en knude, n, og dens underordnede knudepunkter, venstre og højre, er også selv max heaps, så er det fantastisk, vi har en max heap. Hvis dette ikke er tilfældet i hele træet, så har vi ikke en max bunke. Max Heapify-algoritmen bruges til at sortere træet, så det overholder maxheap-principperne. Max Heapify virker kun på én node. Hvis kravet er, at arrayet er et max heap-array, skal alle undertræer konverteres til maxheap før roden, et ad gangen. Algoritmen skal bruges på hver knude. Dette vil blive gjort på N/2 noder (blade vil overholde de maksimale heap-krav). Tidskompleksiteten af ​​heapen er O(NlogN), og for en knude i højden X er tidskompleksiteten O(X). Den følgende kode viser, hvordan man maxheapify et træ (en matrix).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Giver output: I denne kode er theArray oprettet og fyldt med tal. Et andet array, newArray , oprettes, og denne gang vil det indeholde resultatet af metoden, maxheapCreate , max heap-arrayet. Metoden maxHeapCreate kaldes fra main , og her oprettes et nyt array, theNewArr , som udfyldes med maxHeapify- resultaterne. Dette gøres ved at sløjfe over halvdelen af ​​input-arrayets størrelse. For hver gang i løkken kaldes metoden maxHeapify , der starter ved elementet i midten af ​​arrayet og slutter med det første. For hvert opkald af maxHeapify, det venstre underordnede og det højre underordnede underordnede knudepunkt, i, findes, og der foretages kontrol for at finde, hvilken der er den største ud af de tre, idet den defineres som maxVal . Hvis maxVal ikke er lig med den overordnede node, så foretages en swap, så den overordnede node og maxVal byttes, og så kaldes maxHeapify igen denne gang på maxVal og de samme trin udføres som før. Til sidst vil den maksimale heap blive oprettet, og der vil ikke være flere iterationer at udføre. Det opdaterede array, array , returneres nu til main som newArray og derefter udskrives hvert på hinanden følgende element til konsollen. newArrayer nu en max bunke. Bemærk, at som i det foregående eksempel ved brug af PriorityQueue skrives tallene ud: rod, højre-barn af rod som forælder, venstre-barn af rod som forælder, højre-barn af første højre-barn som forælder, venstre-barn af første venstre-barn som forælder, højre-barn af første venstre-barn som forælder, venstre-barn af første højre-barn som forælder, osv. De er i en lidt anden rækkefølge end dem, når du bruger PriorityQueue, fordi sammenligningen foretages mellem på hinanden følgende elementer hvorimod noden i maxheapify-eksemplet sammenlignes med de næste to på hinanden følgende elementer i arrayet og byttes til den største værdi. Kort sagt bruges to forskellige algoritmer. Begge skaber en max bunke.

Konklusion

Så her har vi kigget på max heap og hvordan det kan oprettes med enten en PriorityQueue eller en Max Heapify algoritme. Brug af PriorityQueue med reverseOrder() er en smart måde at gøre dette på og den anbefalede metode. Du kan dog studere disse eksempler og skrive dine egne metoder, da dette vil være en god kodningsøvelse, der hjælper dig med at få succes med dit interview til Java Junior.