The Binary Tree
In Java, there are many different types of data structures. The heap is based on a tree structure called a binary tree. A binary tree consists of nodes, each of which can have a maximum of 2 child nodes: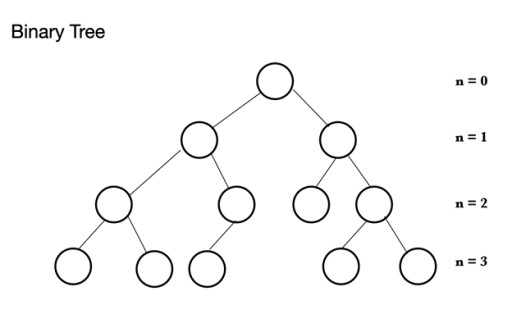 A binary tree consists of a parent node which can have from 0 to 2 nodes. It can have a left-child node and/or a right-child node, or no nodes at all. In a complete binary tree, all nodes are filled except for the last level which can be full, but does not need to be full. The last level, the nth level, can have from 1 to 2n nodes, where the first is at n = 0 and is the root.
A binary tree consists of a parent node which can have from 0 to 2 nodes. It can have a left-child node and/or a right-child node, or no nodes at all. In a complete binary tree, all nodes are filled except for the last level which can be full, but does not need to be full. The last level, the nth level, can have from 1 to 2n nodes, where the first is at n = 0 and is the root.
Max Heap
Max heap (or maxheap) is a complete binary tree. The important thing about it is that the parent node MUST have a value greater than or equal to that of the left- and right-child nodes. If this is not adhered to, you do not have a max heap. Min heap, on the other hand, is the opposite with the root as the smallest value with successive nodes increasing in value; each child node has a value greater than or equal to its parent. It is also a complete binary tree. An example of a max heap is: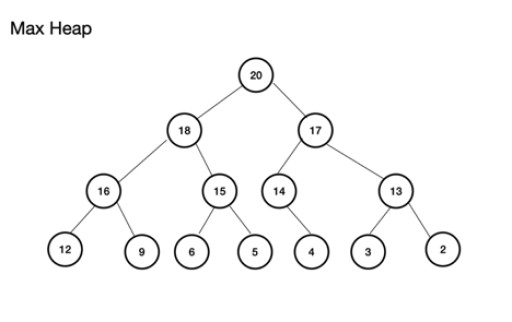 Max heap can be built from an array. This array will be thought of in terms of a tree. For a heap, if the root, (top parent node of the tree) is stored at position (index) n, it is defined for array, theArray, as theArray[n]. The left- and right-child nodes are, therefore, at theArray[2n+1] and theArray[2n+2] respectively. For the max heap, the root is at theArray[0]. For the level n, root n = 0:
theArr[n] is the parent node
theArr[(2*n)+1] is the left child node
theArr[(2*n)+2] is the right child node
Max heap can be built from an array. This array will be thought of in terms of a tree. For a heap, if the root, (top parent node of the tree) is stored at position (index) n, it is defined for array, theArray, as theArray[n]. The left- and right-child nodes are, therefore, at theArray[2n+1] and theArray[2n+2] respectively. For the max heap, the root is at theArray[0]. For the level n, root n = 0:
theArr[n] is the parent node
theArr[(2*n)+1] is the left child node
theArr[(2*n)+2] is the right child nodeThe PriorityQueue Class
Heaps in Java can be implemented using the PriorityQueue Class. PriorityQueues are used to find the most or least important item in a collection.The PriorityQueue class can be found in the java.util.package. PriorityQueues must be formed of objects that are comparable so that they are placed in a particular order in the queue. PriorityQueue can have a comparator so that a comparison between the objects is made and the queue formed according to this comparison. An example is:
import java.util.Comparator;
import java.util.PriorityQueue;
public class Main
{
public static void main(String[] args) {
// Create PriorityQueue with comparator for ascending order of array length
PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
Integer [] array1 = {1, 2, 4, 6, 8, 9};
Integer [] array2 = {3, 6, 9};
Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
Integer [] array5 = {4};
//Add the array lengths to intQueue
intQueue.add(array1.length);
intQueue.add(array2.length);
intQueue.add(array3.length);
intQueue.add(array4.length);
intQueue.add(array5.length);
//Write out contents of intQueue as stored
while (intQueue.size() != 0) {
System.out.println(intQueue.remove());
}
}
}
1
3
6
7
11
In this example, the default size of intQueue is 11, so has not been stated (usually the first argument before the comparator) and the comparator has been given as:
(a,b) -> a - b
This will do a comparison between the items in intQueue and sort it into array lengths of ascending order.Implementation of PriorityQueue to Create a Max Heap
The PriorityQueue Class defaults to min heap without a comparator. Min heap is the opposite of max heap and so the root is the smallest value and successive child nodes are larger or equal to the root and subsequent parental nodes. For this reason, for max heap, it is necessary to use reverseOrder() from Java’s Collections framework as the comparator. This will ensure we get a max heap and not a min heap. This Class has useful methods such as add(), contains(), remove(), poll(), and peek().| Method | Description | Time Complexity |
|---|---|---|
| add(J) | Adds element J at end of the tree | O(LogN) |
| remove(J) | Remove value J from tree | O(N) |
| poll() | Removes max element of tree | O(LogN) |
| peek() | Returns root element at top of tree | O(1) |
| contains(J) | Returns true if J is in the queue, false if not | O(N) |
 The following code is an example of how a max heap (maxheap) is created in java. The first thing to do is to fill an array with the values for which the max heap will be created. This is called theArray. Next, a PriorityQueue, theQueue, is created and then the elements from theArray are added to this. This uses the method add(), e.g. theQueue.add(10) to add 10 to the end of the queue.
To illustrate some of the functionality of the PriorityQueue Class, method peek() is then used to find the head of the heap, and this is the maximum value, in this case, 99. The next task is to check the size of the heap using size() which is found to be 9 and this is printed out to the console.
Method writeMaxHeap writes out the elements in the queue in order of root, left-child with root as parent, right-child with root as parent, left-child with first left-child as parent, right-child with first left-child as parent, right-child with first right-child as parent, left-child with first right-child as parent etc, with subsequent values using the left and right children as parents in the same the order as above.
The PriorityQueue method contains(J) is used to find out whether a specific element, J, is in a queue. In this case we look for J = 10. In our example, it is true that this is in the queue so this is written out to the console as true. Another PriorityQueue method, remove(J) is then used to remove J = 10 from theQueue.
To illustrate more of the functionality of PriorityQueue, method poll() is used to remove the head element (maximum value) using a while loop, each time removing the head element in the new queue and decreasing the queue in size by one each time. This happens in method writeQueue called from main. Each time the element removed is printed to the console. The original queue will eventually have no elements left. The printed elements are the max heap in descending order of value, where the head of the queue is printed out each time.
The following code is an example of how a max heap (maxheap) is created in java. The first thing to do is to fill an array with the values for which the max heap will be created. This is called theArray. Next, a PriorityQueue, theQueue, is created and then the elements from theArray are added to this. This uses the method add(), e.g. theQueue.add(10) to add 10 to the end of the queue.
To illustrate some of the functionality of the PriorityQueue Class, method peek() is then used to find the head of the heap, and this is the maximum value, in this case, 99. The next task is to check the size of the heap using size() which is found to be 9 and this is printed out to the console.
Method writeMaxHeap writes out the elements in the queue in order of root, left-child with root as parent, right-child with root as parent, left-child with first left-child as parent, right-child with first left-child as parent, right-child with first right-child as parent, left-child with first right-child as parent etc, with subsequent values using the left and right children as parents in the same the order as above.
The PriorityQueue method contains(J) is used to find out whether a specific element, J, is in a queue. In this case we look for J = 10. In our example, it is true that this is in the queue so this is written out to the console as true. Another PriorityQueue method, remove(J) is then used to remove J = 10 from theQueue.
To illustrate more of the functionality of PriorityQueue, method poll() is used to remove the head element (maximum value) using a while loop, each time removing the head element in the new queue and decreasing the queue in size by one each time. This happens in method writeQueue called from main. Each time the element removed is printed to the console. The original queue will eventually have no elements left. The printed elements are the max heap in descending order of value, where the head of the queue is printed out each time.
mport java.util.Collections;
import java.util.PriorityQueue;
public class MaxHeap {
public static void writeQueue(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue, priorityQueue, and remove them using poll()
while(priorityQueue.size() != 0)
{
System.out.println(priorityQueue.poll());
}
}
public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue as a max heap - root, left child, right child, etc
for (Integer element : priorityQueue) {
System.out.println(element);
}
}
public static void main(String args[])
{
// Array of numbers to create a max heap array from
int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
// theQueue is created
PriorityQueue<Integer> theQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());
// Elements are added to theQueue
for (int i = 0 ; i <theArray.length; ++i)
{
theQueue.add(theArray[i]);
}
// The head or root element (priority element) is printed out
System.out.println("The root value is : " + theQueue.peek());
// Find size of theQueue. Use method size()
Integer s = theQueue.size();
System.out.println("Size of theQueue? " + s);
// All elements of theQueue are printed in terms of parent,
// left child, right child
System.out.println("theQueue written using for loop:");
writeMaxHeap(theQueue);
// Does theQueue contain 10? Use method contains()
boolean b = theQueue.contains(10);
System.out.println("Does theQueue contain 10? " + b);
// Erasing value 10 from array using remove()
theQueue.remove(10);
// All elements of theQueue are printed out and removed.
// Each one is the maximum value left in the queue.
// At the end theQueue will be empty
System.out.println("theQueue written out using poll():");
writeQueue(theQueue);
// Find size of theQueue. Use method size()
s = theQueue.size();
System.out.println("Size of theQueue? " + s);
}
}
The root value is : 99
Size of theQueue? 9
theQueue written using for loop
99
51
19
13
10
5
6
3
9
Does theQueue contain 10? true
theQueue written out using poll()
99
51
19
13
9
6
5
3
Size of theQueue? 0
Max Heapify
The Max Heapify algorithm is used to ensure that a binary tree is a max heap. If we are at a node, n, and its child nodes, left and right are also max heaps themselves, then great, we have a max heap. If this is not the case throughout the tree then we do not have a max heap. The Max Heapify algorithm is used to sort the tree so that it adheres to maxheap principles. Max Heapify works on only one node. If the requirement is that the array is a max heap array, then all sub trees must be converted to maxheap before the root, one at a time. The algorithm must be used on each node. This will be done on N/2 nodes (leaves will adhere to the max heap requirements). The time complexity of the heap is O(NlogN), and for one node at height X, the time complexity is O(X). The following code shows how to maxheapify a tree (an array).
public class MaxHeapify
{
public static Integer[] maxHeapify(Integer[ ] array, Integer i)
{
// Create left-child and right-child for the node in question
Integer leftChild = 2 * i + 1;
Integer rightChild = 2 * i + 2;
// Assign maxVal to parent node, i
Integer maxVal = i;
// Set maxVal to greater of the two: node or left-child
if( leftChild < array.length && array[leftChild] > array[maxVal] )
maxVal = leftChild;
// Set maxVal to greater of the two: maxVal or right-child
if( rightChild < array.length && array[rightChild] > array[maxVal] )
maxVal = rightChild;
// Check if maxVal is not equal to parent node, then set parent node to
// maxVal, swap values and then do a maxheapify on maxVal
// which is now the previous parent node
if( maxVal != i )
{
Integer value = array[i];
array[i] = array[maxVal];
array[maxVal] = value;
array = maxHeapify(array, maxVal);
}
return array;
}
public static Integer[] maxHeapCreate(Integer array[])
{
// Call maxHeapify to arrange array in a max heap
Integer [] theNewArr = array;
for( Integer i = array.length/2; i >= 0; i-- )
theNewArr = maxHeapify(array, i);
return theNewArr;
}
public static void main(String[] args)
{
// Create array to be maxheapified, theArray,
// and array, newArray, to write results into, by calling maxheapCreate
// newArray will now be a maxheap
Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
Integer[ ] newArray = maxHeapCreate(theArray);
// Print out contents of newArray
System.out.println("newArray:");
for(int i = 0; i < newArray.length; ++i)
{
System.out.println(newArray[i]);
}
// Print out labelled contents of newArray
System.out.println(" root : " + newArray[0]);
for (int i = 0; i <= newArray.length/2 - 1; i++) {
System.out.print(" parent node : " + newArray[i] + " left child : " +
newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
System.out.println();
}
}
}
newArray:
99
51
19
10
3
13
6
5
9
root : 99
parent node : 99 left child : 51 right child :19
parent node : 51 left child : 10 right child :3
parent node : 19 left child : 13 right child :6
parent node : 10 left child : 5 right child :9
In this code, theArray is created and filled with numbers. A second array, newArray, is created and this time it will contain the result of the method, maxheapCreate, the max heap array. Method maxHeapCreate is called from main, and here a new array, theNewArr, is created and filled with the maxHeapify results. This is done by looping over half the size of the input array. For each pass of the loop, method maxHeapify, is called starting at the element in the middle of the array and ending with the first. For each call of maxHeapify, the left child and right child of the parent node, i, are found and checks are done to find which is the biggest out of the three, defining that as maxVal. If maxVal is not equal to the parent node then a swap is done so that the parent node and maxVal are swapped and then maxHeapify is called again this time on maxVal and the same steps carried out as before. Eventually the max heap will be created and there will be no more iterations to carry out.
The updated array, array, is now returned to main as newArray and then each consecutive element printed out to the console. newArray is now a max heap. Note, that as in the previous example using PriorityQueue the numbers are written out: root, right-child of root as parent, left-child of root as parent, right-child of first right-child as parent, left-child of first left-child as parent, right-child of first left-child as parent, left-child of first right-child as parent, etc. They are in a slightly different order to those when using PriorityQueue because the comparison is done between consecutive elements whereas in the maxheapify example, the node is compared to the next two successive elements in the array and swapped for the largest value. In short, two different algorithms are used. Both create a max heap.

GO TO FULL VERSION