Max Heap em Java

A Árvore Binária

Em Java, existem muitos tipos diferentes de estruturas de dados. A pilha é baseada em uma estrutura de árvore chamada árvore binária . Uma árvore binária consiste em nós, cada um dos quais pode ter no máximo 2 nós filhos: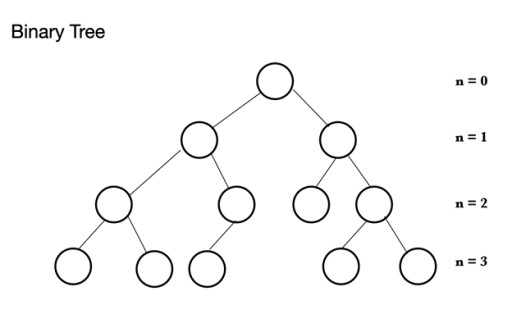 Uma árvore binária consiste em um nó pai que pode ter de 0 a 2 nós. Ele pode ter um nó filho esquerdo e/ou um nó filho direito ou nenhum nó. Em uma árvore binária completa, todos os nós são preenchidos, exceto o último nível que pode estar cheio, mas não precisa estar cheio. O último nível, o enésimo nível, pode ter de 1 a 2n nós, onde o primeiro está em n = 0 e é a raiz.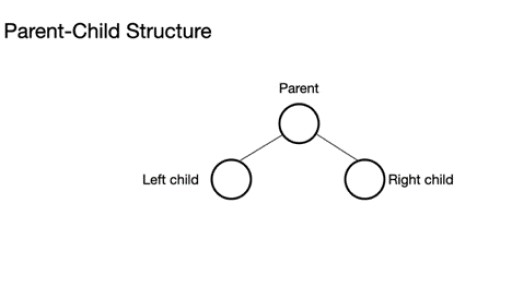

pilha máxima

Max heap (ou maxheap) é uma árvore binária completa . O importante é que o nó pai DEVE ter um valor maior ou igual ao dos nós filho esquerdo e direito. Se isso não for respeitado, você não terá um heap máximo. Min heap, por outro lado, é o oposto com a raiz como o menor valor com nós sucessivos aumentando de valor; cada nó filho tem um valor maior ou igual ao seu pai. É também uma árvore binária completa. Um exemplo de heap máximo é: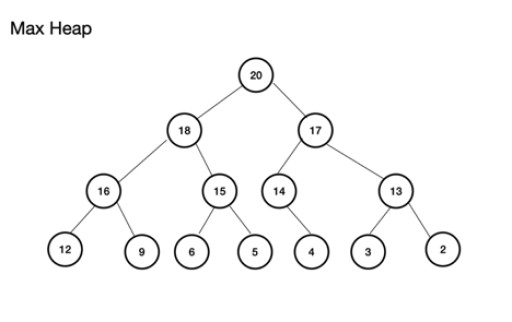 O heap máximo pode ser construído a partir de um array. Esta matriz será pensada em termos de uma árvore. Para um heap, se a raiz (nó pai superior da árvore) for armazenada na posição (índice) n, ela será definida para array, theArray , como theArray[n]. Os nós filho esquerdo e direito estão, portanto, em theArray[2n+1] e theArray[2n+2] respectivamente. Para o heap máximo, a raiz está em theArray[0] . Para o nível n, raiz n = 0: theArr[n] é o nó pai theArr[(2*n)+1] é o nó filho esquerdo theArr[(2*n)+2] é o nó filho direito

A classe PriorityQueue

Heaps em Java podem ser implementados usando a Classe PriorityQueue . PriorityQueues são usados ​​para localizar o item mais ou menos importante em uma coleção. A classe PriorityQueue pode ser encontrada no java.util.package . As PriorityQueues devem ser formadas por objetos comparáveis ​​para que sejam colocados em uma ordem específica na fila. PriorityQueue pode ter um comparador para que seja feita uma comparação entre os objetos e a fila formada de acordo com essa comparação. Um exemplo é:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Dando saída: Neste exemplo, o tamanho padrão de intQueue é 11, portanto não foi declarado (geralmente o primeiro argumento antes do comparador) e o comparador foi fornecido como: Isso fará uma comparação entre os itens em intQueue e os classificará em tamanhos de array de ordem crescente.

Implementação de PriorityQueue para criar um heap máximo

O padrão da classe PriorityQueue é min heap sem um comparador. O heap mínimo é o oposto do heap máximo e, portanto, a raiz é o menor valor e os nós filhos sucessivos são maiores ou iguais à raiz e aos nós pais subsequentes. Por esta razão, para heap máximo, é necessário usar reverseOrder() do framework Collections do Java como comparador. Isso garantirá que obtenhamos um heap máximo e não um heap mínimo. Essa classe tem métodos úteis como add() , contains() , remove() , poll() e peek() . Os elementos são adicionados à fila e podem estar em qualquer ordem. A nova fila PriorityQueue armazenará esses elementos como um heap máximo na ordem inversa. Quando a fila for escrita, a ordem será: Root Filho esquerdo com root como pai (filho esquerdo_1) filho direito com root como pai (filho direito_1) filho esquerdo com filho esquerdo_1 como pai (filho esquerdo_2 ) Filho direito com filho esquerdo_1 como pai (filho direito_2) filho esquerdo com filho direito_1 como pai (filho esquerdo_3) filho direito com filho direito_1 como pai (filho direito_3) filho esquerdo com filho esquerdo_2 como pai (filho esquerdo_4) filho direito com filho esquerdo_2 como pai (filho direito_4), etc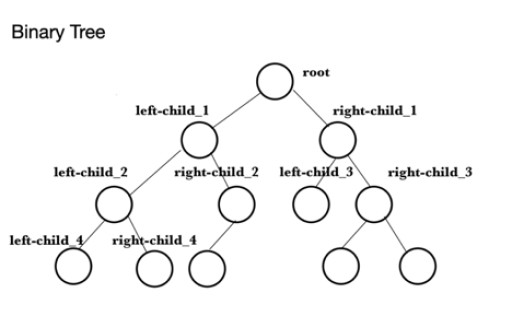O código a seguir é um exemplo de como um heap máximo (maxheap) é criado em java. A primeira coisa a fazer é preencher um array com os valores para os quais o heap máximo será criado. Isso é chamado de Array . Em seguida, uma PriorityQueue , theQueue , é criada e, em seguida, os elementos do theArray são adicionados a ela. Isso usa o método add() , por exemplo , theQueue.add(10) para adicionar 10 ao final da fila. Para ilustrar algumas das funcionalidades da classe PriorityQueue , o método peek() é então usado para encontrar a cabeça do heap, e este é o valor máximo, neste caso, 99. A próxima tarefa é verificar o tamanho do heap usando tamanho()que é encontrado como 9 e isso é impresso no console. O método writeMaxHeap escreve os elementos na fila na ordem de raiz, filho esquerdo com raiz como pai, filho direito com raiz como pai, filho esquerdo com primeiro filho esquerdo como pai, filho direito com primeiro filho esquerdo como pai, filho direito com o primeiro filho direito como pai, filho esquerdo com primeiro filho direito como pai, etc., com valores subsequentes usando os filhos esquerdo e direito como pais na mesma ordem acima. O método PriorityQueue contains(J) é usado para descobrir se um elemento específico, J, está em uma fila. Nesse caso, procuramos por J = 10. Em nosso exemplo, é verdade que isso está na fila, então isso é gravado no console como verdadeiro. Outro método PriorityQueue , remove(J) é então usado para remover J = 10 de theQueue . Para ilustrar melhor a funcionalidade de PriorityQueue , o método poll() é usado para remover o elemento head (valor máximo) usando um loop while , sempre removendo o elemento head na nova fila e diminuindo o tamanho da fila em um a cada vez. Isso acontece no método writeQueuechamado de principal. Cada vez que o elemento removido é impresso no console. A fila original eventualmente não terá mais elementos. Os elementos impressos são o heap máximo em ordem decrescente de valor, onde o início da fila é impresso a cada vez.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Saída:

Max Heapify

O algoritmo Max Heapify é usado para garantir que uma árvore binária seja um heap máximo. Se estivermos em um nó, n, e seus nós filhos, esquerdo e direito, também forem heaps máximos, ótimo, teremos um heap máximo. Se esse não for o caso em toda a árvore, não teremos um heap máximo. O algoritmo Max Heapify é usado para classificar a árvore de modo que ela adira aos princípios de maxheap. Max Heapify funciona em apenas um nó. Se o requisito for que a matriz seja uma matriz de heap máximo, todas as subárvores deverão ser convertidas em heap máximo antes da raiz, uma de cada vez. O algoritmo deve ser usado em cada nó. Isso será feito em N/2 nós (as folhas irão aderir aos requisitos de heap máximo). A complexidade de tempo do heap é O(NlogN), e para um nó na altura X, a complexidade de tempo é O(X). O código a seguir mostra como maximizar uma árvore (um array).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Dando saída: Nesse código, oArray é criado e preenchido com números. Um segundo array, newArray , é criado e desta vez conterá o resultado do método, maxheapCreate , o array de heap máximo. O método maxHeapCreate é chamado de main , e aqui uma nova matriz, theNewArr , é criada e preenchida com os resultados de maxHeapify . Isso é feito fazendo um loop com metade do tamanho do array de entrada. Para cada passagem do loop, o método maxHeapify , é chamado começando no elemento no meio da matriz e terminando com o primeiro. Para cada chamada de maxHeapify, o filho esquerdo e o filho direito do nó pai, i, são encontrados e as verificações são feitas para descobrir qual é o maior dos três, definindo-o como maxVal . Se maxVal não for igual ao nó pai, uma troca é feita para que o nó pai e maxVal sejam trocados e, em seguida, maxHeapify é chamado novamente desta vez em maxVal e as mesmas etapas executadas como antes. Eventualmente, o heap máximo será criado e não haverá mais iterações a serem realizadas. A matriz atualizada, array , agora é retornada para main como newArray e, em seguida, cada elemento consecutivo é impresso no console. newArrayagora é uma pilha máxima. Observe que, como no exemplo anterior usando PriorityQueue, os números são escritos: raiz, filho direito da raiz como pai, filho esquerdo da raiz como pai, filho direito do primeiro filho direito como pai, filho esquerdo do primeiro filho esquerdo como pai, filho direito do primeiro filho esquerdo como pai, filho esquerdo do primeiro filho direito como pai, etc. Eles estão em uma ordem ligeiramente diferente daquela ao usar PriorityQueue porque a comparação é feita entre elementos consecutivos enquanto no exemplo maxheapify, o nó é comparado aos próximos dois elementos sucessivos na matriz e trocado pelo maior valor. Em suma, dois algoritmos diferentes são usados. Ambos criam um heap máximo.

Conclusão

Portanto, aqui examinamos o heap máximo e como ele pode ser criado com um algoritmo PriorityQueue ou Max Heapify. Usar PriorityQueue com reverseOrder() é uma maneira simples de fazer isso e o método recomendado. No entanto, você pode estudar esses exemplos e escrever seus próprios métodos, pois esse será um bom exercício de codificação para ajudá-lo a ter sucesso em sua entrevista para o Java Junior.