Der Binärbaum
In Java gibt es viele verschiedene Arten von Datenstrukturen. Der Heap basiert auf einer Baumstruktur, die als Binärbaum bezeichnet wird . Ein Binärbaum besteht aus Knoten, von denen jeder maximal 2 untergeordnete Knoten haben kann: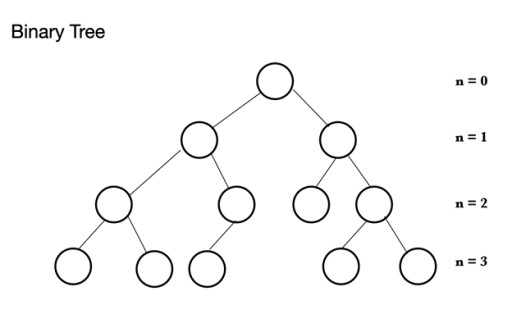
Ein Binärbaum besteht aus einem übergeordneten Knoten, der 0 bis 2 Knoten haben kann. Es kann einen linken untergeordneten Knoten und/oder einen rechten untergeordneten Knoten oder überhaupt keine Knoten haben. In einem vollständigen Binärbaum sind alle Knoten gefüllt, mit Ausnahme der letzten Ebene, die voll sein kann, aber nicht voll sein muss. Die letzte Ebene, die n-te Ebene, kann 1 bis 2n Knoten haben, wobei der erste bei n = 0 liegt und die Wurzel darstellt.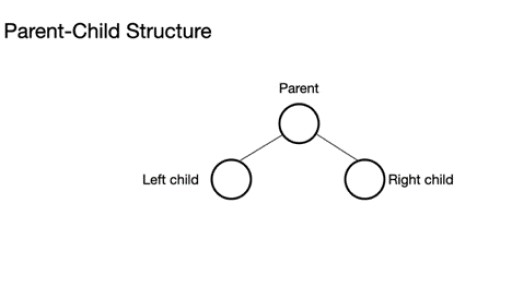
Max Heap
Max Heap (oder Maxheap) ist ein vollständiger Binärbaum . Wichtig dabei ist, dass der übergeordnete Knoten einen Wert haben MUSS, der größer oder gleich dem der linken und rechten untergeordneten Knoten ist. Wenn dies nicht eingehalten wird, haben Sie keinen maximalen Heap. Min Heap hingegen ist das Gegenteil, wobei die Wurzel den kleinsten Wert hat und aufeinanderfolgende Knoten an Wert gewinnen; Jeder untergeordnete Knoten hat einen Wert, der größer oder gleich dem seines übergeordneten Knotens ist. Es ist auch ein vollständiger Binärbaum. Ein Beispiel für einen Max-Heap ist: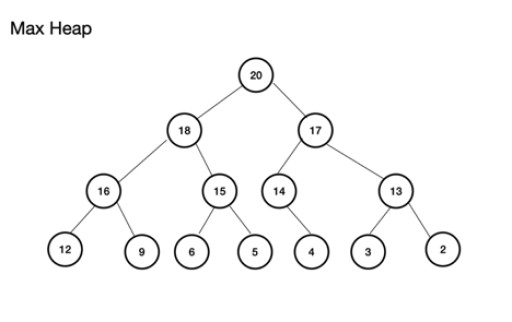
Max-Heap kann aus einem Array erstellt werden. Dieses Array wird in Form eines Baums betrachtet. Wenn bei einem Heap die Wurzel (oberster übergeordneter Knoten des Baums) an Position (Index) n gespeichert ist, wird sie für das Array theArray als theArray [n] definiert.. Die linken und rechten untergeordneten Knoten befinden sich daher jeweils bei theArray[2n+1] und theArray[2n+2] . Für den maximalen Heap liegt der Stamm bei theArray[0] . Für die Ebene n ist Wurzel n = 0: theArr[n] ist der übergeordnete Knoten, theArr[(2*n)+1] ist der linke untergeordnete Knoten, theArr[(2*n)+2] ist der rechte untergeordnete Knoten
Die PriorityQueue-Klasse
Heaps in Java können mithilfe der PriorityQueue- Klasse implementiert werden. PriorityQueues werden verwendet, um das wichtigste oder unwichtigste Element in einer Sammlung zu finden. Die PriorityQueue- Klasse befindet sich im java.util.package . PriorityQueues müssen aus vergleichbaren Objekten bestehen, damit sie in einer bestimmten Reihenfolge in der Warteschlange platziert werden. PriorityQueue kann über einen Komparator verfügen, so dass ein Vergleich zwischen den Objekten durchgeführt und die Warteschlange entsprechend diesem Vergleich gebildet wird. Ein Beispiel ist:
import java.util.Comparator;
import java.util.PriorityQueue;
public class Main
{
public static void main(String[] args) {
// Create PriorityQueue with comparator for ascending order of array length
PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
Integer [] array1 = {1, 2, 4, 6, 8, 9};
Integer [] array2 = {3, 6, 9};
Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
Integer [] array5 = {4};
//Add the array lengths to intQueue
intQueue.add(array1.length);
intQueue.add(array2.length);
intQueue.add(array3.length);
intQueue.add(array4.length);
intQueue.add(array5.length);
//Write out contents of intQueue as stored
while (intQueue.size() != 0) {
System.out.println(intQueue.remove());
}
}
}
1
3
6
7
11
In diesem Beispiel beträgt die Standardgröße von intQueue 11 und wurde daher nicht angegeben (normalerweise das erste Argument vor dem Komparator), und der Komparator wurde wie folgt angegeben:
(a,b) -> a - b
Dadurch wird ein Vergleich zwischen den Elementen in intQueue durchgeführt und in aufsteigender Reihenfolge in Array-Längen sortiert.
Implementierung von PriorityQueue zum Erstellen eines Max Heap
Die PriorityQueue- Klasse ist standardmäßig auf „Min Heap“ ohne Komparator eingestellt. Min. Heap ist das Gegenteil von Max. Heap, daher ist die Wurzel der kleinste Wert und aufeinanderfolgende untergeordnete Knoten sind größer oder gleich der Wurzel und den nachfolgenden übergeordneten Knoten. Aus diesem Grund ist es für den maximalen Heap erforderlich, reverseOrder() aus dem Collections-Framework von Java als Komparator zu verwenden. Dadurch wird sichergestellt, dass wir einen maximalen Heap und keinen minimalen Heap erhalten. Diese Klasse verfügt über nützliche Methoden wie add() , enthält() , remove() , poll() und peek() .| Methode | Beschreibung | Zeitkomplexität |
|---|---|---|
| add(J) | Fügt Element J am Ende des Baums hinzu | O(LogN) |
| entfernen(J) | Entfernen Sie den Wert J aus dem Baum | AN) |
| Umfrage() | Entfernt das maximale Element des Baums | O(LogN) |
| spähen() | Gibt das Wurzelelement oben im Baum zurück | O(1) |
| enthält(J) | Gibt true zurück, wenn J in der Warteschlange ist, andernfalls false | AN) |
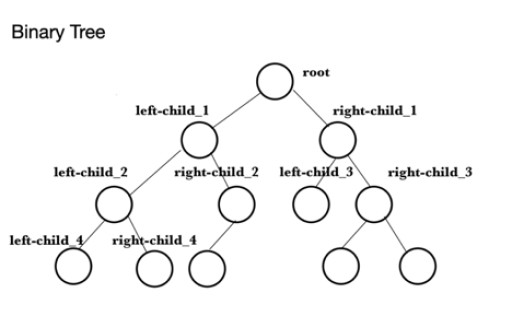Der folgende Code ist ein Beispiel dafür, wie ein Max-Heap (Maxheap) in Java erstellt wird. Als Erstes muss ein Array mit den Werten gefüllt werden, für die der maximale Heap erstellt wird. Dies wird als Array bezeichnet . Als nächstes wird eine PriorityQueue , theQueue , erstellt und dann werden die Elemente aus theArray zu dieser hinzugefügt. Dies verwendet die Methode add() , z. B. theQueue.add(10) , um 10 am Ende der Warteschlange hinzuzufügen. Um einige der Funktionen der PriorityQueue- Klasse zu veranschaulichen, wird dann die Methode peek() verwendet, um den Kopf des Heaps zu finden. Dies ist der Maximalwert, in diesem Fall 99. Die nächste Aufgabe besteht darin, die Größe des Heaps zu überprüfen mit size()Es wird festgestellt, dass es 9 ist, und dies wird auf der Konsole ausgedruckt. Die Methode writeMaxHeap schreibt die Elemente in der Warteschlange in der Reihenfolge Root, linkes Kind mit Root als Elternteil, rechtes Kind mit Root als Elternteil, linkes Kind mit erstem linken Kind als Elternteil, rechtes Kind mit erstem linken Kind als Elternteil Elternteil, rechtes Kind mit erstem rechten Kind als Elternteil, linkes Kind mit erstem rechten Kind als Elternteil usw., wobei nachfolgende Werte das linke und rechte Kind als Eltern in derselben Reihenfolge wie oben verwenden.
mport java.util.Collections;
import java.util.PriorityQueue;
public class MaxHeap {
public static void writeQueue(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue, priorityQueue, and remove them using poll()
while(priorityQueue.size() != 0)
{
System.out.println(priorityQueue.poll());
}
}
public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue as a max heap - root, left child, right child, etc
for (Integer element : priorityQueue) {
System.out.println(element);
}
}
public static void main(String args[])
{
// Array of numbers to create a max heap array from
int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
// theQueue is created
PriorityQueue<Integer> theQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());
// Elements are added to theQueue
for (int i = 0 ; i <theArray.length; ++i)
{
theQueue.add(theArray[i]);
}
// The head or root element (priority element) is printed out
System.out.println("The root value is : " + theQueue.peek());
// Find size of theQueue. Use method size()
Integer s = theQueue.size();
System.out.println("Size of theQueue? " + s);
// All elements of theQueue are printed in terms of parent,
// left child, right child
System.out.println("theQueue written using for loop:");
writeMaxHeap(theQueue);
// Does theQueue contain 10? Use method contains()
boolean b = theQueue.contains(10);
System.out.println("Does theQueue contain 10? " + b);
// Erasing value 10 from array using remove()
theQueue.remove(10);
// All elements of theQueue are printed out and removed.
// Each one is the maximum value left in the queue.
// At the end theQueue will be empty
System.out.println("theQueue written out using poll():");
writeQueue(theQueue);
// Find size of theQueue. Use method size()
s = theQueue.size();
System.out.println("Size of theQueue? " + s);
}
}
Der Wurzelwert ist: 99
Größe der Warteschlange? 9
theQueue geschrieben mit for-Schleife
99
51
19
13
10
5
6
3
9
Enthält theQueue 10? true
theQueue ausgeschrieben mit poll()
99
51
19
13
9
6
5
3
Größe der Warteschlange? 0
Max Heapify
Der Max Heapify-Algorithmus wird verwendet, um sicherzustellen, dass ein Binärbaum ein maximaler Heap ist. Wenn wir uns an einem Knoten n befinden und seine untergeordneten Knoten links und rechts ebenfalls selbst maximale Heaps sind, dann haben wir großartig einen maximalen Heap. Wenn dies im gesamten Baum nicht der Fall ist, haben wir keinen maximalen Heap. Der Max Heapify-Algorithmus wird verwendet, um den Baum so zu sortieren, dass er den Maxheap-Prinzipien entspricht. Max Heapify funktioniert nur auf einem Knoten. Wenn die Anforderung besteht, dass es sich bei dem Array um ein Max-Heap-Array handelt, müssen alle Unterbäume nacheinander vor dem Stamm in Maxheap konvertiert werden. Der Algorithmus muss auf jedem Knoten verwendet werden. Dies erfolgt auf N/2 Knoten (Blätter halten sich an die maximalen Heap-Anforderungen). Die zeitliche Komplexität des Heaps beträgt O(NlogN) und für einen Knoten auf der Höhe X beträgt die zeitliche Komplexität O(X). Der folgende Code zeigt, wie man einen Baum (ein Array) maxheapifiziert.
public class MaxHeapify
{
public static Integer[] maxHeapify(Integer[ ] array, Integer i)
{
// Create left-child and right-child for the node in question
Integer leftChild = 2 * i + 1;
Integer rightChild = 2 * i + 2;
// Assign maxVal to parent node, i
Integer maxVal = i;
// Set maxVal to greater of the two: node or left-child
if( leftChild < array.length && array[leftChild] > array[maxVal] )
maxVal = leftChild;
// Set maxVal to greater of the two: maxVal or right-child
if( rightChild < array.length && array[rightChild] > array[maxVal] )
maxVal = rightChild;
// Check if maxVal is not equal to parent node, then set parent node to
// maxVal, swap values and then do a maxheapify on maxVal
// which is now the previous parent node
if( maxVal != i )
{
Integer value = array[i];
array[i] = array[maxVal];
array[maxVal] = value;
array = maxHeapify(array, maxVal);
}
return array;
}
public static Integer[] maxHeapCreate(Integer array[])
{
// Call maxHeapify to arrange array in a max heap
Integer [] theNewArr = array;
for( Integer i = array.length/2; i >= 0; i-- )
theNewArr = maxHeapify(array, i);
return theNewArr;
}
public static void main(String[] args)
{
// Create array to be maxheapified, theArray,
// and array, newArray, to write results into, by calling maxheapCreate
// newArray will now be a maxheap
Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
Integer[ ] newArray = maxHeapCreate(theArray);
// Print out contents of newArray
System.out.println("newArray:");
for(int i = 0; i < newArray.length; ++i)
{
System.out.println(newArray[i]);
}
// Print out labelled contents of newArray
System.out.println(" root : " + newArray[0]);
for (int i = 0; i <= newArray.length/2 - 1; i++) {
System.out.print(" parent node : " + newArray[i] + " left child : " +
newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
System.out.println();
}
}
}
neuesArray:
99
51
19
10
3
13
65
9
Wurzel: 99
Elternknoten: 99 linkes Kind: 51 rechtes Kind: 19
Elternknoten: 51 linkes Kind: 10 rechtes Kind: 3
Elternknoten: 19 linkes Kind: 13 rechtes Kind: 6
Elternknoten: 10 linkes Kind: 5 rechts Kind :9
In diesem Code wird das Array erstellt und mit Zahlen gefüllt. Ein zweites Array, newArray , wird erstellt und dieses Mal enthält es das Ergebnis der Methode maxheapCreate , das Max-Heap-Array. Die Methode maxHeapCreate wird von main aus aufgerufen und hier wird ein neues Array, theNewArr , erstellt und mit den maxHeapify- Ergebnissen gefüllt. Dies erfolgt durch eine Schleife über die Hälfte der Größe des Eingabearrays. Bei jedem Durchlauf der Schleife wird die Methode maxHeapify aufgerufen, beginnend beim Element in der Mitte des Arrays und endend beim ersten. Für jeden Aufruf von maxHeapify, das linke Kind und das rechte Kind des übergeordneten Knotens, i, werden gefunden und überprüft, welches der drei das größte ist, wobei es als maxVal definiert wird . Wenn maxVal nicht mit dem übergeordneten Knoten übereinstimmt, wird ein Austausch durchgeführt, sodass der übergeordnete Knoten und maxVal ausgetauscht werden. Anschließend wird maxHeapify erneut aufgerufen, dieses Mal für maxVal , und es werden die gleichen Schritte wie zuvor ausgeführt. Schließlich wird der maximale Heap erstellt und es müssen keine weiteren Iterationen durchgeführt werden. Das aktualisierte Array array wird nun als newArray an main zurückgegeben und dann wird jedes aufeinanderfolgende Element an der Konsole ausgegeben. neuesArrayist jetzt ein maximaler Heap. Beachten Sie, dass wie im vorherigen Beispiel mit PriorityQueue die Zahlen ausgeschrieben werden: Wurzel, rechtes Kind von Wurzel als Elternteil, linkes Kind von Wurzel als Elternteil, rechtes Kind von erstem, rechtes Kind als Elternteil, linkes Kind von erstem linkes untergeordnetes Element als übergeordnetes Element, rechtes untergeordnetes Element des ersten linken untergeordneten Elements als übergeordnetes Element, linkes untergeordnetes Element des ersten rechten untergeordneten Elements als übergeordnetes Element usw. Sie sind in einer etwas anderen Reihenfolge als bei der Verwendung von PriorityQueue, da der Vergleich zwischen aufeinanderfolgenden Elementen erfolgt wohingegen im Maxheapify-Beispiel der Knoten mit den nächsten beiden aufeinanderfolgenden Elementen im Array verglichen und gegen den größten Wert ausgetauscht wird. Kurz gesagt, es werden zwei verschiedene Algorithmen verwendet. Beide erstellen einen maximalen Heap.
GO TO FULL VERSION