Java 中的最大堆

二叉樹

在 Java 中，有許多不同類型的數據結構。堆基於稱為二叉樹的樹結構。二叉樹由節點組成，每個節點最多可以有 2 個子節點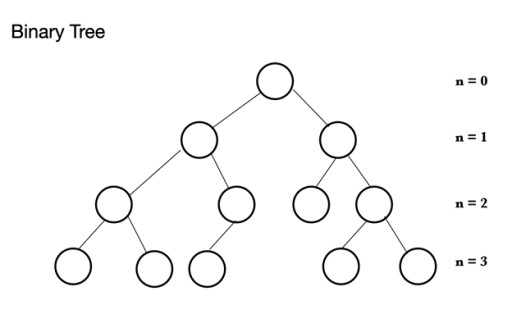：二叉樹由一個父節點組成，父節點可以有 0 到 2 個節點。它可以有一個左子節點和/或一個右子節點，或者根本沒有節點。在一棵完全二叉樹中，除了最後一層可以滿，但不需要滿，所有節點都被填滿。最後一層，即第 n 層，可以有 1 到 2n 個節點，其中第一個節點在 n = 0 處並且是根。

最大堆

最大堆（或maxheap）是一棵完全二叉樹。重要的是父節點的值必須大於或等於左子節點和右子節點的值。如果不遵守這一點，則您沒有最大堆。而最小堆則相反，根為最小值，連續節點的值遞增；每個子節點的值都大於或等於其父節點。也是完全二叉樹。最大堆的一個示例是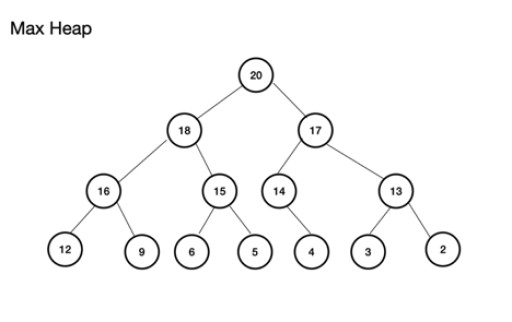：最大堆可以從數組構建。這個數組將被認為是一棵樹。對於堆，如果根（樹的頂部父節點）存儲在位置（索引）n，則為數組theArray定義為theArray[n]. 因此，左子節點和右子節點分別位於theArray[2n+1]和theArray[2n+2]處。對於最大堆，根位於theArray[0]處。對於n層，root n = 0： theArr[n]為父節點 theArr[(2*n)+1]為左子節點 theArr[(2*n)+2]為右子節點

優先隊列類

Java 中的堆可以使用PriorityQueue類來實現。PriorityQueues用於查找集合中最重要或最不重要的項目。可以在java.util.package中找到PriorityQueue類。PriorityQueues必須由可比較的對象組成，以便它們在隊列中按特定順序放置。PriorityQueue可以有一個比較器，以便在對象之間進行比較，並根據此比較形成隊列。一個例子是：

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

給出輸出： 在此示例中， intQueue 的默認大小為 11，因此沒有說明（通常是比較器之前的第一個參數）並且比較器已給出為： 這將在intQueue 中的項目之間進行比較，並將其排序為升序排列的數組長度。

實現 PriorityQueue 創建最大堆

PriorityQueue類默認為沒有比較器的最小堆。最小堆與最大堆相反，因此根是最小值，後續子節點大於或等於根和後續父節點。因此，對於最大堆，有必要使用Java 的 Collections 框架中的reverseOrder()作為比較器。這將確保我們獲得最大堆而不是最小堆。此類具有有用的方法，例如add()、contains()、remove()、poll()和peek()。 元素被添加到隊列中並且可以按任何順序排列。新的 PriorityQueue 隊列將這些元素以相反的順序存儲為最大堆。當隊列被寫出時，順序將是： Root Left-child with root as parent (Left-child_1) Right-child with root as parent (Right-child_1) Left-child with Left-child_1 parent (Left-child_2 ) Right-child with Left-child_1 as parent (Right-child_2) Left-child with Right-child_1 as parent (Left-child_3) Right-child with Right-child_1 as parent (Right-child_3) Left-child with Left-child_2作為父母 (Left-child_4) Right-child with Left-child_2 作為父母 (Right-child_4) 等下面的代碼是java中如何創建最大堆（maxheap）的一個例子。要做的第一件事是用將為其創建最大堆的值填充一個數組。這稱為theArray。接下來，創建一個PriorityQueue theQueue ，然後將theArray中的元素添加到其中。這使用方法add()，例如theQueue.add(10)將 10 添加到隊列的末尾。為了說明PriorityQueue類的一些功能，然後使用方法peek()查找堆頭，這是最大值，在本例中為 99。下一個任務是檢查堆的大小使用尺寸（）發現它是 9 並將其打印到控制台。writeMaxHeap方法按照根順序寫出隊列中的元素，以根為父的左子，以根為父的右子，以第一個左子為父的左子，以第一個左子為右子的右子parent, right-child with first right-child as parent, left-child with first right-child as parent etc, 隨後的值使用左右孩子作為父母，順序與上述相同。 PriorityQueue方法contains(J)用於查找特定元素 J 是否在隊列中。在本例中，我們尋找 J = 10。在我們的示例中，它確實在隊列中，因此它被寫入控制台為真。然後使用另一個PriorityQueue方法remove(J)從theQueue中刪除 J = 10 。為了說明PriorityQueue的更多功能，方法poll()用於使用while循環刪除頭元素（最大值），每次刪除新隊列中的頭元素，每次都將隊列大小減一。這發生在方法writeQueue中從主要調用。每次刪除的元素都會打印到控制台。原始隊列最終將沒有任何元素。打印的元素是按值降序排列的最大堆，每次都打印出隊列的頭部。

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

輸出：

最大堆積

Max Heapify 算法用於確保二叉樹是最大堆。如果我們在一個節點 n 處，它的子節點 left 和 right 本身也是最大堆，那麼很好，我們有一個最大堆。如果整個樹都不是這種情況，那麼我們就沒有最大堆。Max Heapify 算法用於對樹進行排序，使其遵循最大堆原則。Max Heapify 僅適用於一個節點。如果要求數組是最大堆數組，那麼所有的子樹都必須在根之前轉換為最大堆，一次一個。該算法必須在每個節點上使用。這將在 N/2 個節點上完成（葉子將遵守最大堆要求）。堆的時間複雜度是O(NlogN)，對於一個高度為X的節點，時間複雜度是O(X)。下面的代碼顯示瞭如何 maxheapify 一棵樹（一個數組）。

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

給出輸出： 在此代碼中，創建了theArray並用數字填充。創建第二個數組newArray，這次它將包含方法maxheapCreate的結果，即最大堆數組。方法maxHeapCreate從main調用，這裡創建了一個新數組theNewArr並用maxHeapify結果填充。這是通過循環輸入數組大小的一半來完成的。對於循環的每次傳遞，調用方法maxHeapify從數組中間的元素開始並以第一個元素結束。對於maxHeapify的每次調用，找到父節點 i 的左孩子和右孩子，並進行檢查以找出三者中最大的一個，將其定義為maxVal。如果maxVal不等於父節點，則進行交換，以便交換父節點和maxVal，然後這次在maxVal上再次調用maxHeapify，並執行與之前相同的步驟。最終將創建最大堆，並且將不再執行迭代。更新後的數組 array現在作為newArray返回到main ，然後將每個連續的元素打印到控制台。新數組現在是最大堆。請注意，在前面使用PriorityQueue 的示例中，數字被寫出：根，根的右子作為父，根的左子作為父，第一個右子的右子作為父，第一個的左子左孩子作為父母，第一個左孩子的右孩子作為父母，第一個右孩子的左孩子作為父母，等等。它們的順序與使用PriorityQueue時的順序略有不同，因為比較是在連續元素之間進行的而在 maxheapify 示例中，節點與數組中接下來的兩個連續元素進行比較，並交換最大值。簡而言之，使用了兩種不同的算法。兩者都創建一個最大堆。

結論

所以在這裡我們已經了解了最大堆以及如何使用PriorityQueue或 Max Heapify 算法創建它。將PriorityQueue與reverseOrder()結合使用是一種巧妙的方法，也是推薦的方法。但是，您可以研究這些示例並編寫自己的方法，因為這將是一個很好的編碼練習，可以幫助您在 Java Junior 面試中取得成功。