Montón máximo en Java

El árbol binario

En Java, hay muchos tipos diferentes de estructuras de datos. El montón se basa en una estructura de árbol denominada árbol binario . Un árbol binario consta de nodos, cada uno de los cuales puede tener un máximo de 2 nodos secundarios: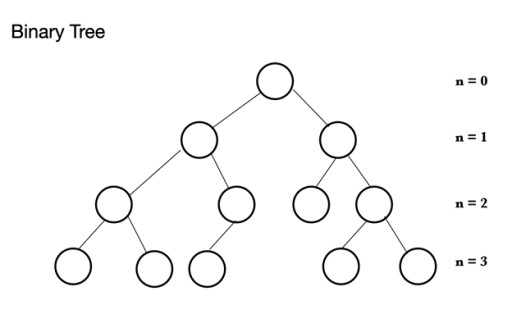 Un árbol binario consta de un nodo principal que puede tener de 0 a 2 nodos. Puede tener un nodo secundario izquierdo y/o un nodo secundario derecho, o no tener ningún nodo. En un árbol binario completo, todos los nodos están llenos excepto el último nivel que puede estar lleno, pero no necesita estarlo. El último nivel, el n-ésimo nivel, puede tener de 1 a 2n nodos, donde el primero está en n = 0 y es la raíz.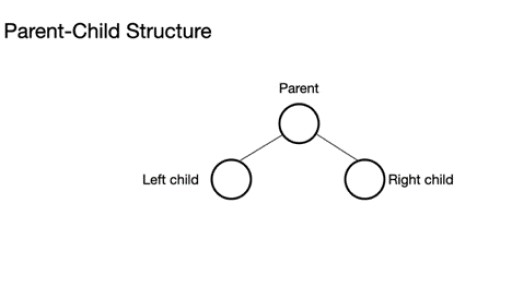

Montón máximo

Max heap (o maxheap) es un árbol binario completo . Lo importante de esto es que el nodo principal DEBE tener un valor mayor o igual que el de los nodos secundarios izquierdo y derecho. Si esto no se cumple, no tiene un montón máximo. Min heap, por otro lado, es lo opuesto con la raíz como el valor más pequeño con nodos sucesivos aumentando en valor; cada nodo hijo tiene un valor mayor o igual que su padre. También es un árbol binario completo. Un ejemplo de un montón máximo es: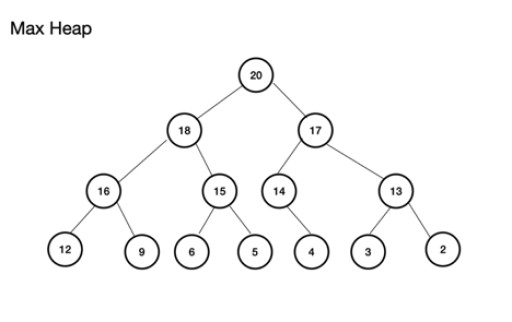 El montón máximo se puede construir a partir de una matriz. Esta matriz se considerará en términos de un árbol. Para un montón, si la raíz (nodo principal superior del árbol) se almacena en la posición (índice) n, se define para la matriz, theArray , como theArray[n]. Los nodos secundarios izquierdo y derecho están, por lo tanto, en theArray[2n+1] y theArray[2n+2] respectivamente. Para el montón máximo, la raíz está en theArray[0] . Para el nivel n, raíz n = 0: theArr[n] es el nodo principal theArr[(2*n)+1] es el nodo secundario izquierdo theArr[(2*n)+2] es el nodo secundario derecho

La clase PriorityQueue

Los montones en Java se pueden implementar utilizando PriorityQueue Class. PriorityQueues se utilizan para encontrar el elemento más o menos importante en una colección. La clase PriorityQueue se puede encontrar en java.util.package . PriorityQueues debe estar formado por objetos que sean comparables para que se coloquen en un orden particular en la cola. PriorityQueue puede tener un comparador para que se haga una comparación entre los objetos y se forme la cola de acuerdo con esta comparación. Un ejemplo es:

import java.util.Comparator;
import java.util.PriorityQueue;

public class Main
{
    public static void main(String[] args) {
        // Create PriorityQueue with comparator for ascending order of array length
        PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
        Integer [] array1 = {1, 2, 4, 6, 8, 9};
        Integer [] array2 = {3, 6, 9};        
        Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
        Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};   
        Integer [] array5 = {4};

        //Add the array lengths to intQueue
        intQueue.add(array1.length);
        intQueue.add(array2.length);
        intQueue.add(array3.length);
        intQueue.add(array4.length);
        intQueue.add(array5.length);
        //Write out contents of intQueue as stored 
        while (intQueue.size() != 0) {
            System.out.println(intQueue.remove());
        }
    }          
}

Dando salida: En este ejemplo, el tamaño predeterminado de intQueue es 11, por lo que no se ha indicado (generalmente el primer argumento antes del comparador) y el comparador se ha dado como: Esto hará una comparación entre los elementos en intQueue y los clasificará en longitudes de matriz en orden ascendente.

Implementación de PriorityQueue para crear un montón máximo

La clase PriorityQueue tiene como valor predeterminado el montón mínimo sin un comparador. El montón mínimo es lo opuesto al montón máximo y, por lo tanto, la raíz es el valor más pequeño y los nodos secundarios sucesivos son más grandes o iguales que la raíz y los nodos principales posteriores. Por esta razón, para max heap, es necesario usar reverseOrder() del marco de colecciones de Java como comparador. Esto asegurará que obtengamos un montón máximo y no un montón mínimo. Esta clase tiene métodos útiles como add() , contains() , remove() , poll() y peek() . Los elementos se agregan a la cola y pueden estar en cualquier orden. La nueva cola PriorityQueue almacenará esos elementos como un montón máximo en orden inverso. Cuando se escribe la cola, el orden será: Root Left-child con root como padre (Left-child_1) Right-child con root como padre (Right-child_1) Left-child con Left-child_1 como padre (Left-child_2 ) Hijo derecho con Hijo izquierdo_1 como padre (hijo derecho_2) Hijo izquierdo con hijo derecho_1 como padre (hijo izquierdo_3) Hijo derecho con hijo derecho_1 como padre (hijo derecho_3) Hijo izquierdo con hijo izquierdo_2 como padre (Left-child_4) Right-child con Left-child_2 como padre (Right-child_4), etc.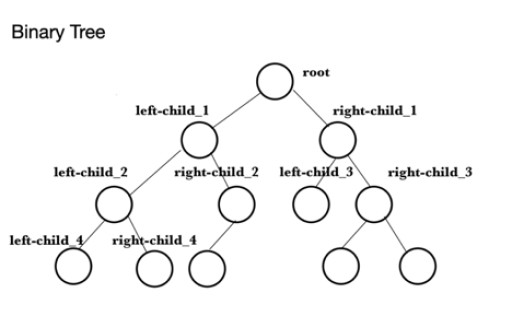El siguiente código es un ejemplo de cómo se crea un montón máximo (maxheap) en Java. Lo primero que debe hacer es llenar una matriz con los valores para los que se creará el montón máximo. Esto se llama elArray . A continuación, se crea un PriorityQueue , theQueue , y luego se le agregan los elementos de theArray . Esto usa el método add() , por ejemplo , theQueue.add(10) para agregar 10 al final de la cola. Para ilustrar parte de la funcionalidad de PriorityQueue Class, se usa el método peek() para encontrar el encabezado del montón, y este es el valor máximo, en este caso, 99. La siguiente tarea es verificar el tamaño del montón. usando tamaño ()que resulta ser 9 y esto se imprime en la consola. El método writeMaxHeap escribe los elementos en la cola en orden de raíz, hijo izquierdo con raíz como padre, hijo derecho con raíz como padre, hijo izquierdo con el primer hijo izquierdo como padre, hijo derecho con el primer hijo izquierdo como padre, hijo derecho con el primer hijo derecho como padre, hijo izquierdo con el primer hijo derecho como padre, etc., con valores posteriores usando los hijos izquierdo y derecho como padres en el mismo orden que el anterior. El método PriorityQueue contains(J) se utiliza para averiguar si un elemento específico, J, está en una cola. En este caso, buscamos J = 10. En nuestro ejemplo, es cierto que esto está en la cola, por lo que se escribe en la consola como verdadero. Otro método PriorityQueue , remove(J) se usa para eliminar J = 10 de theQueue . Para ilustrar más la funcionalidad de PriorityQueue , se utiliza el método poll() para eliminar el elemento principal (valor máximo) mediante un bucle while , cada vez que se elimina el elemento principal en la nueva cola y se reduce el tamaño de la cola en uno cada vez. Esto sucede en el método writeQueuellamado desde principal. Cada vez que el elemento eliminado se imprime en la consola. A la cola original finalmente no le quedarán elementos. Los elementos impresos son el montón máximo en orden descendente de valor, donde la cabeza de la cola se imprime cada vez.

mport java.util.Collections;
import java.util.PriorityQueue;

public class MaxHeap {

       public static void writeQueue(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue, priorityQueue, and remove them using poll()
           while(priorityQueue.size() != 0)
           {
               System.out.println(priorityQueue.poll());
           }
       }

       public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
       {
           // Write out elements in queue as a max heap - root, left child, right child, etc
           for (Integer element : priorityQueue) {
               System.out.println(element);
           }
       }

       public static void main(String args[])
       {
           // Array of numbers to create a max heap array from
           int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};

           // theQueue is created
           PriorityQueue<Integer> theQueue =
                   new PriorityQueue<Integer>(Collections.reverseOrder());

           // Elements are added to theQueue
           for (int i = 0 ; i <theArray.length; ++i)
           {
               theQueue.add(theArray[i]);
           }

           // The head or root element (priority element) is printed out
           System.out.println("The root value is : " +  theQueue.peek());

           // Find size of theQueue. Use method size()
           Integer s = theQueue.size();
           System.out.println("Size of theQueue? " + s);

           // All elements of theQueue are printed in terms of parent,
           // left child, right child
           System.out.println("theQueue written using for loop:");
           writeMaxHeap(theQueue);

           // Does theQueue contain 10? Use method contains()
           boolean b = theQueue.contains(10);
           System.out.println("Does theQueue contain 10? " + b);

           // Erasing value 10 from array using remove()
           theQueue.remove(10);

           // All elements of theQueue are printed out and removed.
           // Each one is the maximum value left in the queue.
           // At the end theQueue will be empty
           System.out.println("theQueue written out using poll():");
           writeQueue(theQueue);

           // Find size of theQueue. Use method size()
           s = theQueue.size();
           System.out.println("Size of theQueue? " + s);
       }
   }

Producción:

Máx.

El algoritmo Max Heapify se usa para garantizar que un árbol binario sea un montón máximo. Si estamos en un nodo, n, y sus nodos secundarios, izquierdo y derecho, también son montones máximos, entonces genial, tenemos un montón máximo. Si este no es el caso en todo el árbol, entonces no tenemos un montón máximo. El algoritmo Max Heapify se usa para ordenar el árbol de modo que se adhiera a los principios de maxheap. Max Heapify funciona en un solo nodo. Si el requisito es que la matriz sea una matriz de almacenamiento dinámico máximo, entonces todos los subárboles deben convertirse a almacenamiento dinámico máximo antes de la raíz, uno a la vez. El algoritmo debe usarse en cada nodo. Esto se hará en N/2 nodos (las hojas cumplirán con los requisitos máximos de almacenamiento dinámico). La complejidad temporal del montón es O(NlogN), y para un nodo en la altura X, la complejidad temporal es O(X). El siguiente código muestra cómo maximizar un árbol (una matriz).

public class MaxHeapify

{
   public static Integer[] maxHeapify(Integer[ ] array, Integer i)
   {
       // Create left-child and right-child for the node in question
       Integer leftChild = 2 * i + 1;
       Integer rightChild = 2 * i + 2;

       // Assign maxVal to parent node, i
       Integer maxVal = i;

       // Set maxVal to greater of the two: node or left-child
       if( leftChild < array.length && array[leftChild] > array[maxVal] )
           maxVal = leftChild;

       // Set maxVal to greater of the two: maxVal or right-child
       if( rightChild < array.length && array[rightChild] > array[maxVal] )
           maxVal = rightChild;

       // Check if maxVal is not equal to parent node, then set parent node to
       // maxVal, swap values and then do a maxheapify on maxVal
       // which is now the previous parent node
       if( maxVal != i )
       {
           Integer value = array[i];
           array[i] = array[maxVal];
           array[maxVal] = value;
           array = maxHeapify(array, maxVal);
       }

       return array;
   }


   public static Integer[] maxHeapCreate(Integer array[])
   {
       // Call maxHeapify to arrange array in a max heap
       Integer [] theNewArr = array;
       for( Integer i = array.length/2; i >= 0; i-- )
           theNewArr = maxHeapify(array, i);

       return theNewArr;
   }

   public static void main(String[] args)
   {
       // Create array to be maxheapified, theArray,
       // and array, newArray, to write results into, by calling maxheapCreate
       // newArray will now be a maxheap
       Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
       Integer[ ] newArray = maxHeapCreate(theArray);

       // Print out contents of newArray
       System.out.println("newArray:");
       for(int i = 0; i < newArray.length; ++i)
       {
           System.out.println(newArray[i]);
       }

       // Print out labelled contents of newArray
       System.out.println(" root : " + newArray[0]);
       for (int i = 0; i <= newArray.length/2 - 1; i++) {
           System.out.print(" parent node : " + newArray[i] + " left child : " +
                            newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
           System.out.println();
       }
  }
}

Dando salida: En este código, theArray se crea y se llena con números. Se crea una segunda matriz, newArray , y esta vez contendrá el resultado del método, maxheapCreate , la matriz de pila máxima. Se llama al método maxHeapCreate desde main , y aquí se crea una nueva matriz, theNewArr , y se llena con los resultados de maxHeapify . Esto se hace mediante un bucle de más de la mitad del tamaño de la matriz de entrada. Para cada paso del ciclo, se llama al método maxHeapify , comenzando en el elemento en el medio de la matriz y terminando en el primero. Para cada llamada de maxHeapify, se encuentran el hijo izquierdo y el hijo derecho del nodo principal, i, y se realizan comprobaciones para encontrar cuál es el más grande de los tres, definiéndolo como maxVal . Si maxVal no es igual al nodo principal, se realiza un intercambio para que el nodo principal y maxVal se intercambien y luego se vuelve a llamar a maxHeapify esta vez en maxVal y se llevan a cabo los mismos pasos que antes. Eventualmente, se creará el montón máximo y no habrá más iteraciones para llevar a cabo. La matriz actualizada, matriz , ahora se devuelve a main como newArray y luego cada elemento consecutivo se imprime en la consola. nueva matrizahora es un montón máximo. Tenga en cuenta que, como en el ejemplo anterior con PriorityQueue, los números se escriben: raíz, hijo derecho de la raíz como padre, hijo izquierdo de la raíz como padre, hijo derecho del primer hijo derecho como padre, hijo izquierdo del primero hijo izquierdo como padre, hijo derecho del primer hijo izquierdo como padre, hijo izquierdo del primer hijo derecho como padre, etc. Están en un orden ligeramente diferente al que se usa cuando se usa PriorityQueue porque la comparación se realiza entre elementos consecutivos mientras que en el ejemplo de maxheapify, el nodo se compara con los siguientes dos elementos sucesivos en la matriz y se intercambia por el valor más grande. En resumen, se utilizan dos algoritmos diferentes. Ambos crean un montón máximo.

Conclusión

Así que aquí hemos analizado el montón máximo y cómo se puede crear con un algoritmo PriorityQueue o Max Heapify. Usar PriorityQueue con reverseOrder() es una buena manera de hacer esto y el método recomendado. Sin embargo, puede estudiar estos ejemplos y escribir sus propios métodos, ya que este será un buen ejercicio de codificación que lo ayudará a tener éxito en su entrevista para Java Junior.