Cây nhị phân
Trong Java, có nhiều kiểu cấu trúc dữ liệu khác nhau. Heap dựa trên một cấu trúc cây được gọi là cây nhị phân . Cây nhị phân bao gồm các nút, mỗi nút có thể có tối đa 2 nút con: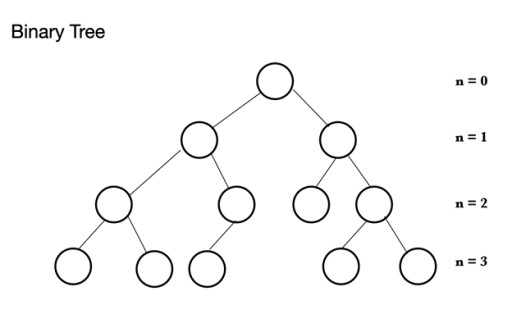
Cây nhị phân gồm một nút cha có thể có từ 0 đến 2 nút. Nó có thể có nút con trái và/hoặc nút con phải hoặc không có nút nào cả. Trong một cây nhị phân đầy đủ, tất cả các nút đều được lấp đầy ngoại trừ mức cuối cùng có thể đầy, nhưng không cần phải đầy. Mức cuối cùng, mức thứ n, có thể có từ 1 đến 2n nút, trong đó nút đầu tiên ở mức n = 0 và là gốc.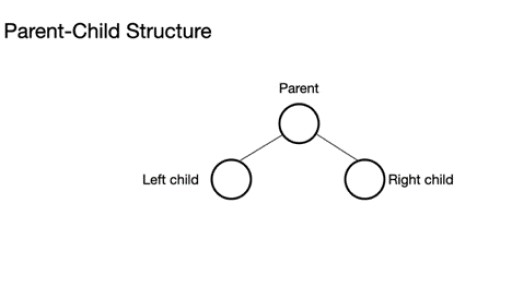
đống tối đa
Max heap (hoặc maxheap) là một cây nhị phân hoàn chỉnh . Điều quan trọng về nó là nút cha PHẢI có giá trị lớn hơn hoặc bằng giá trị của nút con trái và con phải. Nếu điều này không được tuân thủ, bạn không có một đống tối đa. Mặt khác, heap tối thiểu thì ngược lại với gốc là giá trị nhỏ nhất với các nút liên tiếp tăng giá trị; mỗi nút con có giá trị lớn hơn hoặc bằng nút cha của nó. Nó cũng là một cây nhị phân hoàn chỉnh. Một ví dụ về max heap là: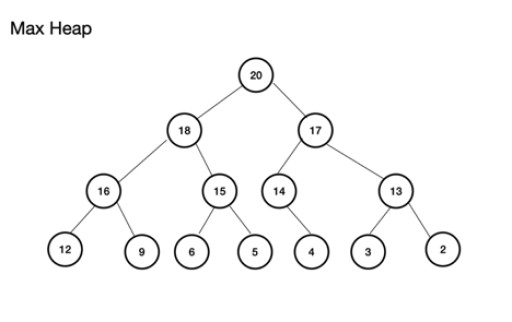
Max heap có thể được tạo từ một mảng. Mảng này sẽ được coi là một cái cây. Đối với một đống, nếu gốc, (nút cha trên cùng của cây) được lưu trữ tại vị trí (chỉ mục) n, thì nó được xác định cho mảng, theArray , dưới dạng theArray[n]. Do đó, các nút con trái và phải lần lượt là theArray[2n+1] và theArray[2n+2] . Đối với heap tối đa, gốc là theArray[0] . Đối với cấp n, gốc n = 0: theArr[n] là nút cha theArr[(2*n)+1] là nút con bên trái theArr[(2*n)+2] là nút con bên phải
Lớp PriorityQueue
Heaps trong Java có thể được triển khai bằng Lớp PriorityQueue . PriorityQueues được sử dụng để tìm mục quan trọng nhất hoặc ít quan trọng nhất trong một bộ sưu tập. Bạn có thể tìm thấy lớp PriorityQueue trong java.util.package . PriorityQueues phải được hình thành từ các đối tượng có thể so sánh được để chúng được đặt theo một thứ tự cụ thể trong hàng đợi. PriorityQueue có thể có một bộ so sánh để thực hiện so sánh giữa các đối tượng và hàng đợi được hình thành theo so sánh này. Một ví dụ là:
import java.util.Comparator;
import java.util.PriorityQueue;
public class Main
{
public static void main(String[] args) {
// Create PriorityQueue with comparator for ascending order of array length
PriorityQueue intQueue = new PriorityQueue((a,b) -> a - b);
Integer [] array1 = {1, 2, 4, 6, 8, 9};
Integer [] array2 = {3, 6, 9};
Integer [] array3 = {2, 4, 8, 16, 32, 64, 128};
Integer [] array4 = {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55};
Integer [] array5 = {4};
//Add the array lengths to intQueue
intQueue.add(array1.length);
intQueue.add(array2.length);
intQueue.add(array3.length);
intQueue.add(array4.length);
intQueue.add(array5.length);
//Write out contents of intQueue as stored
while (intQueue.size() != 0) {
System.out.println(intQueue.remove());
}
}
}
1
3
6
7
11
Trong ví dụ này, kích thước mặc định của intQueue là 11, do đó không được nêu rõ (thường là đối số đầu tiên trước bộ so sánh) và bộ so sánh đã được đưa ra là:
(a,b) -> a - b
Điều này sẽ thực hiện so sánh giữa các mục trong intQueue và sắp xếp nó thành độ dài mảng theo thứ tự tăng dần.
Triển khai PriorityQueue để tạo Max Heap
Lớp PriorityQueue mặc định là heap tối thiểu mà không có bộ so sánh. Heap tối thiểu ngược lại với heap tối đa và do đó, gốc là giá trị nhỏ nhất và các nút con liên tiếp lớn hơn hoặc bằng nút gốc và các nút gốc tiếp theo. Vì lý do này, đối với heap tối đa, cần phải sử dụng reverseOrder() từ khung công tác Bộ sưu tập của Java làm công cụ so sánh. Điều này sẽ đảm bảo chúng tôi nhận được một đống tối đa chứ không phải một đống tối thiểu. Lớp này có các phương thức hữu ích như add() , contains() , remove() , poll() và peek() .| Phương pháp | Sự miêu tả | Thời gian phức tạp |
|---|---|---|
| thêm(J) | Thêm phần tử J vào cuối cây | O(LogN) |
| loại bỏ(J) | Xóa giá trị J khỏi cây | TRÊN) |
| thăm dò ý kiến() | Xóa phần tử tối đa của cây | O(LogN) |
| nhìn lén() | Trả về phần tử gốc ở đầu cây | Ô(1) |
| chứa(J) | Trả về true nếu J ở trong hàng đợi, false nếu không | TRÊN) |
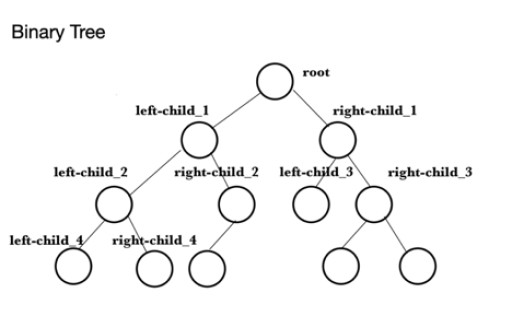Đoạn mã sau là một ví dụ về cách một đống tối đa (maxheap) được tạo ra trong java. Điều đầu tiên cần làm là điền vào một mảng các giá trị mà heap tối đa sẽ được tạo. Cái này được gọi là theArray . Tiếp theo, một PriorityQueue , theQueue , được tạo và sau đó các phần tử từ theArray được thêm vào phần này. Điều này sử dụng phương thức add() , ví dụ theQueue.add(10) để thêm 10 vào cuối hàng đợi. Để minh họa một số chức năng của Lớp PriorityQueue , phương thức peek() sau đó được sử dụng để tìm phần đầu của heap và đây là giá trị lớn nhất, trong trường hợp này là 99. Nhiệm vụ tiếp theo là kiểm tra kích thước của heap sử dụng kích thước()được tìm thấy là 9 và điều này được in ra bàn điều khiển. Phương thức writeMaxHeap ghi ra các phần tử trong hàng đợi theo thứ tự gốc, con trái với gốc là cha, con phải với gốc là cha, con trái với con trái đầu tiên là cha, con phải với con trái đầu tiên là cha cha mẹ, con phải với con phải đầu tiên là cha mẹ, con trái với con phải đầu tiên là cha mẹ, v.v., với các giá trị tiếp theo sử dụng con trái và con phải làm cha mẹ theo thứ tự như trên.
mport java.util.Collections;
import java.util.PriorityQueue;
public class MaxHeap {
public static void writeQueue(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue, priorityQueue, and remove them using poll()
while(priorityQueue.size() != 0)
{
System.out.println(priorityQueue.poll());
}
}
public static void writeMaxHeap(PriorityQueue<Integer> priorityQueue)
{
// Write out elements in queue as a max heap - root, left child, right child, etc
for (Integer element : priorityQueue) {
System.out.println(element);
}
}
public static void main(String args[])
{
// Array of numbers to create a max heap array from
int[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
// theQueue is created
PriorityQueue<Integer> theQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());
// Elements are added to theQueue
for (int i = 0 ; i <theArray.length; ++i)
{
theQueue.add(theArray[i]);
}
// The head or root element (priority element) is printed out
System.out.println("The root value is : " + theQueue.peek());
// Find size of theQueue. Use method size()
Integer s = theQueue.size();
System.out.println("Size of theQueue? " + s);
// All elements of theQueue are printed in terms of parent,
// left child, right child
System.out.println("theQueue written using for loop:");
writeMaxHeap(theQueue);
// Does theQueue contain 10? Use method contains()
boolean b = theQueue.contains(10);
System.out.println("Does theQueue contain 10? " + b);
// Erasing value 10 from array using remove()
theQueue.remove(10);
// All elements of theQueue are printed out and removed.
// Each one is the maximum value left in the queue.
// At the end theQueue will be empty
System.out.println("theQueue written out using poll():");
writeQueue(theQueue);
// Find size of theQueue. Use method size()
s = theQueue.size();
System.out.println("Size of theQueue? " + s);
}
}
Giá trị gốc là: 99
Kích thước của hàng đợi? 9
theQueue được viết bằng vòng lặp for
99
51
19
13
10
5
6
3
9
Hàng đợi có chứa 10 không? ĐÚNG VẬY
theQueue được viết ra bằng cách sử dụng poll()
99
51
19
13
9
6
5
3
Kích thước của hàng đợi? 0
Heapify tối đa
Thuật toán Max Heapify được sử dụng để đảm bảo rằng cây nhị phân là một đống tối đa. Nếu chúng ta đang ở một nút, n và các nút con của nó, trái và phải cũng là các đống tối đa, thì thật tuyệt, chúng ta có một đống tối đa. Nếu đây không phải là trường hợp trong toàn bộ cây thì chúng ta không có một đống tối đa. Thuật toán Max Heapify được sử dụng để sắp xếp cây sao cho nó tuân theo nguyên tắc maxheap. Max Heapify chỉ hoạt động trên một nút. Nếu yêu cầu là mảng là một mảng heap tối đa, thì tất cả các cây con phải được chuyển đổi thành maxheap trước gốc, mỗi lần một cây. Thuật toán phải được sử dụng trên mỗi nút. Điều này sẽ được thực hiện trên N/2 nút (các lá sẽ tuân thủ các yêu cầu về heap tối đa). Độ phức tạp thời gian của heap là O(NlogN) và đối với một nút ở độ cao X, độ phức tạp thời gian là O(X). Đoạn mã sau chỉ ra cách maxheapify một cây (một mảng).
public class MaxHeapify
{
public static Integer[] maxHeapify(Integer[ ] array, Integer i)
{
// Create left-child and right-child for the node in question
Integer leftChild = 2 * i + 1;
Integer rightChild = 2 * i + 2;
// Assign maxVal to parent node, i
Integer maxVal = i;
// Set maxVal to greater of the two: node or left-child
if( leftChild < array.length && array[leftChild] > array[maxVal] )
maxVal = leftChild;
// Set maxVal to greater of the two: maxVal or right-child
if( rightChild < array.length && array[rightChild] > array[maxVal] )
maxVal = rightChild;
// Check if maxVal is not equal to parent node, then set parent node to
// maxVal, swap values and then do a maxheapify on maxVal
// which is now the previous parent node
if( maxVal != i )
{
Integer value = array[i];
array[i] = array[maxVal];
array[maxVal] = value;
array = maxHeapify(array, maxVal);
}
return array;
}
public static Integer[] maxHeapCreate(Integer array[])
{
// Call maxHeapify to arrange array in a max heap
Integer [] theNewArr = array;
for( Integer i = array.length/2; i >= 0; i-- )
theNewArr = maxHeapify(array, i);
return theNewArr;
}
public static void main(String[] args)
{
// Create array to be maxheapified, theArray,
// and array, newArray, to write results into, by calling maxheapCreate
// newArray will now be a maxheap
Integer[] theArray = {5, 3, 13, 10, 99, 19, 6, 51, 9};
Integer[ ] newArray = maxHeapCreate(theArray);
// Print out contents of newArray
System.out.println("newArray:");
for(int i = 0; i < newArray.length; ++i)
{
System.out.println(newArray[i]);
}
// Print out labelled contents of newArray
System.out.println(" root : " + newArray[0]);
for (int i = 0; i <= newArray.length/2 - 1; i++) {
System.out.print(" parent node : " + newArray[i] + " left child : " +
newArray[(2*i)+1] + " right child :" + newArray[(2*i)+2]);
System.out.println();
}
}
}
Mảng mới:
99
51
19
10
3
13
6
5
gốc : 99
nút cha: 99 con trái: 51 con phải: 19
nút cha: 51 con trái: 10 con phải :3
nút cha: 19 con trái: 13 con phải: 6
nút cha: 10 con trái: 5 con phải: 9
Trong mã này, theArray được tạo và điền vào các số. Một mảng thứ hai, newArray , được tạo và lần này nó sẽ chứa kết quả của phương thức, maxheapCreate , mảng heap tối đa. Phương thức maxHeapCreate được gọi từ main và ở đây, một mảng mới, theNewArr , được tạo và chứa đầy các kết quả maxHeapify . Điều này được thực hiện bằng cách lặp hơn một nửa kích thước của mảng đầu vào. Đối với mỗi lần vượt qua vòng lặp, phương thức maxHeapify , được gọi bắt đầu từ phần tử ở giữa mảng và kết thúc bằng phần tử đầu tiên. Đối với mỗi cuộc gọi của maxHeapify, nút con bên trái và nút con bên phải của nút cha, i, được tìm thấy và quá trình kiểm tra được thực hiện để tìm ra nút lớn nhất trong ba nút, xác định nút đó là maxVal . Nếu maxVal không bằng nút cha thì việc hoán đổi được thực hiện để nút cha và maxVal được hoán đổi và sau đó maxHeapify được gọi lại lần này trên maxVal và các bước tương tự được thực hiện như trước đây. Cuối cùng, heap tối đa sẽ được tạo và sẽ không có thêm bước lặp nào để thực hiện. Mảng được cập nhật, mảng , hiện được trả về chính dưới dạng newArray và sau đó mỗi phần tử liên tiếp được in ra bảng điều khiển. Mảng mớibây giờ là một đống tối đa. Lưu ý rằng như trong ví dụ trước khi sử dụng PriorityQueue, các số được viết ra: gốc, con phải của gốc là cha, con trái của gốc là cha, con phải của con phải đầu tiên là cha, con trái của đầu tiên con trái là cha mẹ, con phải của con trái đầu tiên là cha mẹ, con trái của con phải đầu tiên là cha mẹ, v.v. Chúng có thứ tự hơi khác so với thứ tự khi sử dụng PriorityQueue vì việc so sánh được thực hiện giữa các phần tử liên tiếp trong khi trong ví dụ maxheapify, nút được so sánh với hai phần tử liên tiếp tiếp theo trong mảng và đổi chỗ cho giá trị lớn nhất. Nói tóm lại, hai thuật toán khác nhau được sử dụng. Cả hai đều tạo ra một đống tối đa.
GO TO FULL VERSION